Cinemática- MRUV
FísicaMecânica
Prof.Simões
Algumasdefiniçõesparaacinemática
• Vimosqueavelocidademédiarepresentaataxa
médiadevariaçãodoespaçoemrelaçãoaotempo,
istoé:
Δx
vm =
Δt
• Aaceleraçãoseráataxadevariaçãodavelocidade
emrelaçãoaotempo,ouseja:
Δv
am =
Δt
Velocidadeeaceleração
• Avelocidade indicaquantoodeslocamentomuda
comotempo
– Exemplo:v=2m/s->querdizerqueacadasegundoo
corpodeslocou-sede2m.
– Seemt1=0saposiçãoera0m,depoisdeumsegundo
será2,depoisdemaisumserá4,etc.
• Aaceleração indicaquantoavelocidademuda
comotempo
– Exemplo:a=3m/s2->querdizerqueacadasegundoa
velocidadeaumentade3m/s.
– Seemt1=0savelocidadeera0m/s,noinstante1será
3,noinstante2será6m/s,noinstante3será9m/s,
etc.
Exemplo2.2
Solução
Análise
Afastando,acelerando
Afastando,freando
Aproximando,acelerando
Aproximando,freando
Exemplo2.3
𝑣 = 60 + 0,5 ( 𝑡 *
Resolução
Resolução
c)Aceleração instantânea
Planilha
d)Expressão geral daaceleração instantânea
Δv dv
a = lim
=
Δt→0 Δt
dt
d
a = (60+ 0,5t 2 )⇒ a = t
dt
2
a(1)
=
1
m/
s
Demonstraçãográfica
Nográfico vxt,ainclinação dareta
representa aaceleração
Reta secante:aceleração média
Reta tangente:aceleração instantânea
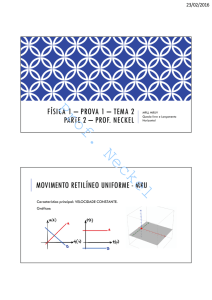
MRUV
• NoMRUV,aaceleraçãoéconstante;odeslocamento
corresponderáaumaparábolaeavelicidade auma
retainclinada.Porexemplo:
Aaceleração é constante
Aposição varia por t2
Avelocidade varia linearmente
Resumo
d
v(t )
dt
d
x(t )
dt
x(t
)
v(t
)
v(t
)
dt
∫
a(t
)
a(t
)
dt
∫
MRUV
• Por exemplo,umcorpo em MRUVdesloca-sedeacordo coma
função abaixo.Calcule sua posição evelocidade para t=2s,e
sua aceleração.
Equações noMRUV– velocidade
• ComonoMRUVaaceleração é constante,
podemos fazer:
EquaçõesdoMRUV– deslocamento(área)
Velocidade
• Nográficovxt,aáreacorrespondeaodeslocamento.
• Porexemplo,sejaumcorpoemMRU,comv=2m/s.Seu
deslocamentoem4segundosserá:
A=Δx
Tempo
EquaçõesdoMRUV– deslocamento(área)
•
•
•
Caso afigura formada formais
complexa,podemos usar o
método daintegração.
Por exemplo,seja umcorpo cuja
velocidade varia deacordo com
afunção v(t)representada.
Calcular seu deslocamentoentre
os instante t=1set=5s.
Odeslocamentocorresponde
numericamente à área soba
curva,que pode ser calculada
por:
t2
Δx = ∫ v(t )dt
t1
A=Δx
EquaçõesdoMRUV– deslocamento(área)
•
•
Por exemplo,acurva ao lado
refere-seà função:
1 3
v(t ) = t − 2t +5
10
Odeslocamentoentret1=1se
t2=5sserá:
⎛ 1 3
⎞
Δx = ∫ ⎜ t − 2t +5⎟ dt
⎝ 10
⎠
5
1
Δx
=
11,6
m
Geogebra
A=Δx=11,6
EquaçõesdoMRUV– deslocamento(área)
• NoMRUV,comoaaceleraçãoéconstante,ográficoda
velocidadeseráumaretainclinada,eodeslocamento(=área)
serádadapor:
Aárea é deumtrapézio:
Aplicando noMRUV:
A=Δx
EquaçõesdoMRUV– equaçãohorária(posição)
EquaçõesdoMRUV– equaçãohorária(posição)
EquaçõesdoMRUV– equaçãohorária(posição)
EquaçõesdoMRUV- Torricelli
EquaçõesdoMRUV- Resumo
• TodososproblemasdeMRUVpoderãoser
resolvidoscomasseguintesfórmulas
Exemplo2.4
Exemplo2.5
Exemplo2.5(esquemaegráfico)
Quedalivre
• Aquedadeumobjetoéummovimentodo
tipoMRUV,emqueaaceleraçãoéumvalor
constanteparapequenasalturas,evale
g=9,81m/s2
• Ovalordegédiferenteparacadaplanetaou
satélite:
– Lua:1,6m/s2
– Sol:270m/s2
– Marte:3,72m/s2
Resolução deproblemas dequeda livre
• Asequações para queda livre são asmesmas
doMRUV
• Seconsiderarmos oeixo y(vertical),fazer a=9,81m/s2
• Quando ocorpo estiver subindo (vpositiva),
sua velocidade diminuirá
• Quando ocorpo estiver descendo (vnegativa),
sua velocidade aumentará
Exemplo 2.6
Exemplo 2.7
e)quanto tempoabolaleva para passar novamente pelo ponto
dearremesso?
f)faça aanálise gráfica doproblema
Exemplo 2.7(esquema)