Lista 5: Derivada como taxa de variação e Diferencial

Lista 5: Derivada como taxa de variação e Diferencial - Cálculo Diferencial e Integral I
Professora: Elisandra Bär de Figueiredo
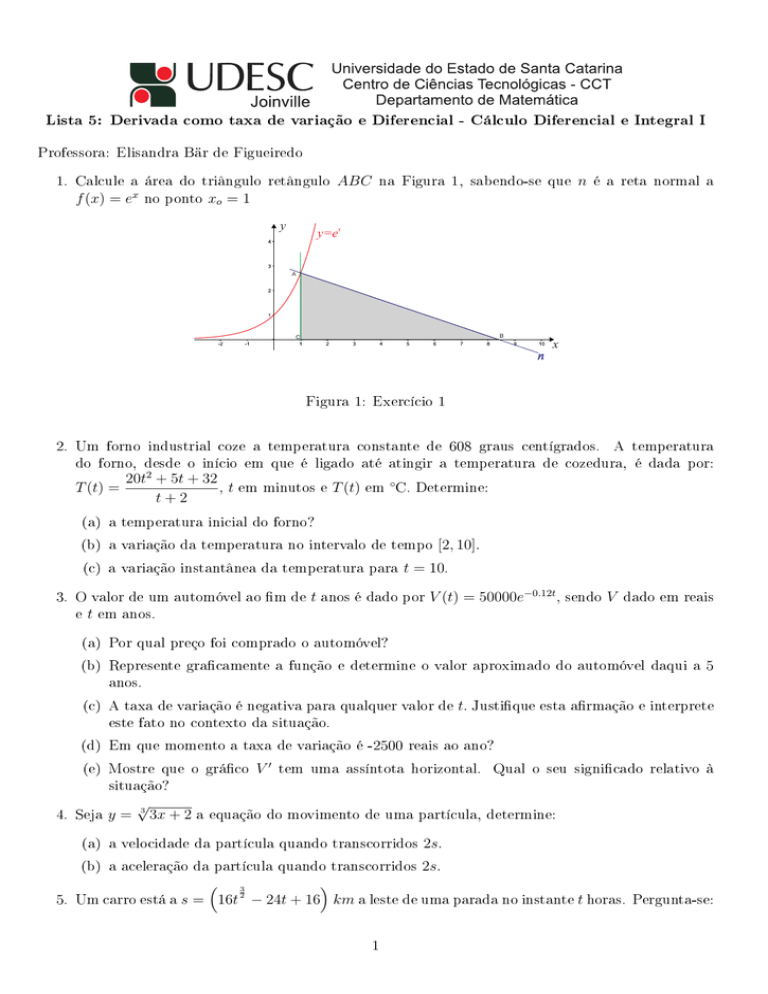
1. Calcule a área do triângulo retângulo ABC na Figura 1, sabendo-se que n é a reta normal a
f (x) = ex no ponto xo = 1
y
x
y=e
x
n
Figura 1: Exercício 1
2. Um forno industrial coze a temperatura constante de 608 graus centígrados. A temperatura
do forno, desde o início em que é ligado até atingir a temperatura de cozedura, é dada por:
T (t) =
20t2 + 5t + 32
, t em minutos e T (t) em ◦ C. Determine:
t+2
(a) a temperatura inicial do forno?
(b) a variação da temperatura no intervalo de tempo [2, 10].
(c) a variação instantânea da temperatura para t = 10.
3. O valor de um automóvel ao m de t anos é dado por V (t) = 50000e−0.12t , sendo V dado em reais
e t em anos.
(a) Por qual preço foi comprado o automóvel?
(b) Represente gracamente a função e determine o valor aproximado do automóvel daqui a 5
anos.
(c) A taxa de variação é negativa para qualquer valor de t. Justique esta armação e interprete
este fato no contexto da situação.
(d) Em que momento a taxa de variação é -2500 reais ao ano?
(e) Mostre que o gráco V ′ tem uma assíntota horizontal. Qual o seu signicado relativo à
situação?
4. Seja y =
√
3
3x + 2 a equação do movimento de uma partícula, determine:
(a) a velocidade da partícula quando transcorridos 2s.
(b) a aceleração da partícula quando transcorridos 2s.
(
3
)
5. Um carro está a s = 16t 2 − 24t + 16 km a leste de uma parada no instante t horas. Pergunta-se:
1
1
4
(a) Qual é a velocidade no instante t = h e qual é o sentido que ele se move?
(b) Qual a posição do carro quando sua velocidade é nula?
6. Dois corpos têm movimento em uma mesma reta segundo as equações s1 = t3 + 4t2 + t − 1 e
s2 = 2t3 − 5t2 + t + 2. Determine a velocidade e as posições desses dois corpos no instante em que
as suas acelerações são iguais. Considere s1 e s2 em metros e t em segundos.
7. Dois pontos partem da origem do eixo x no instante t = 0 e se movem ao longo desse eixo de
acordo com as equações x1 = t2 − 2t e x2 = 8t − t2 , com x1 e x2 em metros e t em segundos.
(a) Em que instante os dois têm mesma velocidade?
(b) Qual a velocidade desses pontos no instante em que eles têm a mesma posição?
8. A posição de uma partícula que se desloca ao longo do eixo y varia com o tempo x segundo a
)
v (
equação y = 0 1 − e−cx , x ≥ 0, onde v0 e c são constantes positivas. Use a DEFINIÇÃO de
c
derivadas para determinar a velocidade da partícula no instante x.
9. Uma esfera aumenta de modo que seu raio cresce a razão de 12, 5 cm/s. Qual a variação do volume
no instante em que o raio é de 15, 2 cm?
10. Dois carros, um dirigindo-se para leste com velocidade de 80 km/h, o outro dirigindo-se para
sul com velocidade de 50 km/h, estão viajando em direção ao encontro das rodovias. A que
velocidade os carros se aproximam um do outro, no momento em que o primeiro carro está a 400
m e o segundo está a 300 m da interseção das rodovias?
11. Um tanque de forma cônica invertido tem altura de 8 m, raio da base 2 m. O mesmo se enche de
água à razão de 7 m3 /min. Com que velocidade sobe o nível da água quando este se encontra a
4 m de profundidade?
12. Uma piscina tem 18 m de largura, 28 m de comprimento, 2 m de profundidade em um extremo e
8 m no outro, o fundo tem forma de um plano inclinado. Se a água está sendo bombeada para a
piscina à razão de 0, 8 m3 /min, com que velocidade se eleva o nível da água no instante em que
ele esta a 1, 8 m na extremidade mais profunda?
13. Em que pontos da parábola y 2 − 18x = 0 a ordenada y cresce duas vezes mais depressa que a
abscissa x?
14. Uma criança esta empinando uma pipa e movendo-se horizontalmente a 4 m/s. Supondo que a
pipa permaneça sempre a 80 m de altura, sobre o nível do solo, qual é a velocidade com que a
criança está soltando a corda da pipa quando esta corda medir 100 m?
Obs : Despreze a altura da criança.
15. Um tanque tem a forma de um cilindro circular reto com raio da base de 5 m e altura de 10 m.
Se instante t = 0s, a água começa a uir no tanque à razão de 25 m3 /h, determine:
(a) com que velocidade sobe o nível da água?
(b) quanto tempo levará para encher o tanque?
16. Um balão está subindo verticalmente acima de uma estrada a uma velocidade constante de
1
m/s. Quando ele está a 17 m acima do solo, uma bicicleta que se desloca a uma velocidade
3
constante de 5 m/s passa por baixo dele. A que taxa a distância entre a bicicleta e o balão
aumentará 3s depois?
2
17. O nível de café que escoa de um ltro cônico, de diâmetro e altura 15 cm, para uma cafeteira
cilíndrica, de diâmetro e altura 15 cm, varia a uma taxa de 2 · 10−4 cm/min. A que taxa o nível
do café, na cafeteira, aumentará quando a altura de café no ltro for 5 cm?
18. Um cabo de cobre tem diâmetro de 1 cm a 0◦ C . Suponha que seu comprimento é de 1 m e não se
altera com a variação da temperatura. Se seu diâmetro aumenta a uma velocidade de 0, 02cm/◦ C,
Calcule a taxa de variação do volume desse cabo quando a temperatura está a 20◦ C .
19. Numa granja de frangos, o abastecimento de ração é automático. A ração está num reservatório
que tem a forma de uma pirâmide de base quadrada com 2 m de lado e 6 m de altura, cujo vértice
está voltado para baixo. Se o consumo de ração é de 0, 05 m3 /h, com que velocidade desce o nível
de ração quando este está a 2 m do vértice?
20. A altura de um triângulo cresce a razão de 1cm/ min e sua área aumenta a razão de 2cm2 / min.
Qual a taxa de variação da base do triângulo quando sua altura for 10cm e sua área 100cm2 .
21. Uma piscina tem 24m de comprimento e seus extremos são trapézios isósceles com altura de 6m,
uma base menor 6m e uma base maior de 8m. A água está sendo bombeada para a piscina à
razão de 10m3 /mim. Com que velocidade o nível de água está subindo quando a profundidade
da água é de 2m?
22. Um avião (A) voa a 124 m/s, paralelamente ao solo, a uma altitude de 1220 m no sentido oeste,
tomando como referência um holofote (H), xado no solo, que o focaliza e que se encontra à
esquerda da projeção vertical (P) do avião e sabendo que a luz do holofote deverá permanecer
iluminando o avião, qual será a velocidade com que θ estará variando quando a distância entre o
holofote e a projeção vertical do avião for de 610 m?
23. Às 7 : 00 horas dois navios partem de um ponto O em rotas que formam um ângulo de 120◦ . Os
navios A e B deslocam-se a 20 km/h e 25km/h, respectivamente. Determine qual é a velocidade
de afastamento desses navios às 9 : 00 horas.
24. Use aproximações
lineares para estimar o valor de
√
4
(a) 17
1
(g) √
2
3
30
(b) (8, 06) 3
−0,13
◦
(h) e
(c) tan(44 )
(i) arctan(1, 02)
(d) ln(1, 05)
√
(j) (1, 01)6
(e) 99, 8
√
(k) 3 65
(f) (1, 2)1,2
25. Suponha que não temos uma fórmula para g(x), mas sabemos que g(2) = −4 e g ′ (x) =
para todo x. Use uma aproximação linear para estimar g(1, 95) e g(2, 05).
√
x2 + 5
26. A aresta de um cubo tem 30cm, com um possível erro de medida de 0,1cm. Use diferenciais para
estimar o erro possível no cálculo
(a) do volume do cubo.
(b) da área da superfície do cubo.
27. Por meio de diferenciais obtenha uma fórmula aproximada do volume de uma na coroa cilíndrica
de altura h, raio interior r e espessura ∆r. Qual o erro decorrente do uso desta fórmula?
28. Estima-se em 12cm o raio de uma esfera com erro máximo de 0,05cm. Estime o erro máximo para
no cálculo do volume da esfera.
3
29. Uma janela tem o formato de um quadrado com um semicírculo em cima. A base da janela mede
60cm com um possível erro na medida de 1mm. Use diferenciais para estimar o maior erro possível
no cálculo da área desta janela.
30. Na medida que a areia escoa de um recipiente, vai formando uma pilha cônica cuja altura é sempre
igual ao raio. Se, num dado instante, o raio é 10cm, use diferenciais para aproximar a variação
do raio que ocasiona um aumento de 2cm3 no volume da pilha.
31. A área de um quadrado de lado s é dada por s2 . Para um acréscimo ∆s de s, ilustre geometricamente dA e ∆A − dA.
32. Aproxime, por meio de diferenciais, N = (2, 01)4 − 3(2, 01)3 + 4(2, 01)2 − 5. Qual o valor exato de
N?
33. Uma caixa em forma de cubo deve ter um revestimento externo com espessura de 1/4 cm. Se o
lado da caixa é de 2 m, usando diferencial, encontre a quantidade de revestimento necessária.
34. Um material está sendo escoado de um recipiente, formando uma pilha cônica cuja altura é sempre
igual ao raio da base. Se em dado instante o raio é 12 cm, use diferenciais para obter a variação
do raio que origina um aumento de 2 cm3 no volume da pilha.
Respostas:
1. A =
e3
u.a.
2
2. .
(a) 16◦ C.
(b) 17,875◦ C.
(c) 19,29◦ C por minuto.
3. .
(a) 50000 reais.
(b)
(c)
(d) 7,3 anos.
(e)
1
4
4. (a) v(2) = u.c./s
(b) a(2) = −
1
u.c./s2
16
5. (a) v(1/4) = −12km/h e está indo na direção oeste
(b) s(1) = 8km
6. t = 3s; v1 (3) = 52m/s; v2 (3) = 25m/s; s1 (3) = 65m; s2 (3) = 14m
7. (a) 2,5s
(b) t = 0s ⇒ v1 = −2cm/s e v2 = 8cm/s; t = 5s ⇒ v1 = 8cm/s e v2 = −2cm/s
8. v0 e−cx u.c./u.t.
9. 11552π cm3 /s
10. 94km/h
4
11.
7
m/min
π
12. 0,005m/min ou 0,025m/min, dependendo da interpretação da piscina.
(
13.
9 9
,
8 2
)
14. 2,4m/s
15. (a)
1
m/h
π
(b) 31,4h
27
≈ 3, 46m/s
61
16. √
17.
2 · 10−4
cm/min
9
18. 1, 4π cm3 /min
19. -0,1125m/h
20. -1,6cm/min
21. 0,0625m/min
22. 0,08rad/s
√
23. 5 61km/h
24. .
(a)
(b)
(c)
(d)
(e)
(f)
65
= 2, 03125
32
4, 02
90 − π
≈ 0, 9651
90
0, 05
9, 99
1, 2
(g)
(h)
(i)
(j)
(k)
26
≈ 0, 32099
81
0, 87
π
1
+
≈ 0, 7954
4 100
1, 06
193
≈ 4, 02083
48
25. g(1, 95) ≈ −4, 15 e g(2, 05) ≈ −3, 85
26. dV = 270cm3 e dA = 36cm2
27. V = 2πrh∆r =(Área lateral do cilindro interior)×(Espessura) e E = πh(∆r)2
28. dV = 28, 8π cm3
29. dA = 16, 7263cm2
30. dr =
1
cm
50π
5
31. A região sombreada corresponde a dA e ∆A − dA está indicado
ΔA-dA
32. N ≈ 3, 12 e N = 3, 12100501
33. 60000 cm3
34. 0,0044209 cm
6