Física 1 – Exercícios de M.U.V. Professora: Dolores 1. (Unicamp

Física 1 – Exercícios de M.U.V.
Professora: Dolores
1. (Unicamp 2014) Correr uma maratona requer preparo físico e determinação. A uma pessoa comum se
recomenda, para o treino de um dia, repetir 8 vezes a seguinte sequência: correr a distância de 1 km à velocidade de
10,8 km/h e, posteriormente, andar rápido a 7,2 km/h durante dois minutos.
a) Qual será a distância total percorrida pelo atleta ao terminar o treino?
b) Para atingir a velocidade de 10,8 km/h, partindo do repouso, o atleta percorre 3 m com aceleração constante.
Calcule o módulo da aceleração a do corredor neste trecho.
2. (Uel 2014) O desrespeito às leis de trânsito, principalmente àquelas relacionadas à velocidade permitida nas vias
públicas, levou os órgãos regulamentares a utilizarem meios eletrônicos de fiscalização: os radares capazes de aferir
a velocidade de um veículo e capturar sua imagem, comprovando a infração ao Código de Trânsito Brasileiro.
Suponha que um motorista trafegue com seu carro à velocidade constante de 30 m/s em uma avenida cuja
velocidade regulamentar seja de 60 km/h. A uma distância de 50 m, o motorista percebe a existência de um radar
fotográfico e, bruscamente, inicia a frenagem com uma desaceleração de 5 m/s2.
Sobre a ação do condutor, é correto afirmar que o veículo
a) não terá sua imagem capturada, pois passa pelo radar com velocidade de 50 km/h.
b) não terá sua imagem capturada, pois passa pelo radar com velocidade de 60 km/h.
c) terá sua imagem capturada, pois passa pelo radar com velocidade de 64 km/h.
d) terá sua imagem capturada, pois passa pelo radar com velocidade de 66 km/h.
e) terá sua imagem capturada, pois passa pelo radar com velocidade de 72 km/h.
3. (Uel 2014) Em uma prova de atletismo, um corredor, que participa da prova de 100 m rasos, parte do repouso,
corre com aceleração constante nos primeiros 50 m e depois mantém a velocidade constante até o final da prova.
Sabendo que a prova foi completada em 10 s, calcule o valor da aceleração, da velocidade atingida pelo atleta no
final da primeira metade da prova e dos intervalos de tempo de cada percurso.
Apresente os cálculos.
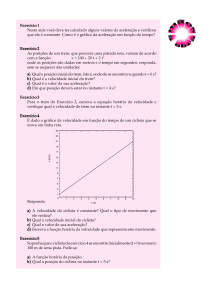
4. (Fuvest 2014) Arnaldo e Batista disputam uma corrida de longa distância. O gráfico das velocidades dos dois
atletas, no primeiro minuto da corrida, é mostrado na figura.
Determine:
a) a aceleração aB de Batista em t = 10 s;
b) as distâncias dA e dB percorridas por Arnaldo e Batista, respectivamente, até t = 50 s;
c) a velocidade média v A de Arnaldo no intervalo de tempo entre 0 e 50 s.
5. (Acafe 2012) Para garantir a segurança no trânsito, deve-se reduzir a velocidade de um veículo em dias de chuva,
senão vejamos: um veículo em uma pista reta, asfaltada e seca, movendo-se com velocidade de módulo 36 km h
10 m s
é freado e desloca-se 5,0 m até parar. Nas mesmas circunstâncias, só que com a pista molhada sob
chuva, necessita de 1,0 m a mais para parar.
Considerando a mesma situação (pista seca e molhada) e agora a velocidade do veículo de módulo 108 km h
 30 m s,
a alternativa correta que indica a distância a mais para parar, em metros, com a pista molhada em relação
a pista seca é:
a) 6
b) 2
c) 1,5
d) 9
6. (Ifsp 2011) Numa determinada avenida onde a velocidade máxima permitida é de 60 km/h, um motorista dirigindo
a 54 km/h vê que o semáforo, distante a 63 metros, fica amarelo e decide não parar. Sabendo-se que o sinal amarelo
permanece aceso durante 3 segundos aproximadamente, esse motorista, se não quiser passar no sinal vermelho,
deverá imprimir ao veículo uma aceleração mínima de ______ m/s2.
O resultado é que esse motorista ______ multado, pois ______ a velocidade máxima.
Assinale a alternativa que preenche as lacunas, correta e respectivamente.
a) 1,4 – não será – não ultrapassará.
b) 4,0 – não será – não ultrapassará.
c) 10 – não será – não ultrapassará.
d) 4,0 – será – ultrapassará.
e) 10 – será – ultrapassará.
7. (Ufpr 2010) Em uma prova internacional de ciclismo, dois dos ciclistas, um francês e, separado por uma distância
de 15 m à sua frente, um inglês, se movimentam com velocidades iguais e constantes de módulo 22 m/s. Considere
agora que o representante brasileiro na prova, ao ultrapassar o ciclista francês, possui uma velocidade constante de
módulo 24 m/s e inicia uma aceleração constante de módulo 0,4 m/s2, com o objetivo de ultrapassar o ciclista inglês e
ganhar a prova. No instante em que ele ultrapassa o ciclista francês, faltam ainda 200 m para a linha de chegada.
Com base nesses dados e admitindo que o ciclista inglês, ao ser ultrapassado pelo brasileiro, mantenha constantes
as características do seu movimento, assinale a alternativa correta para o tempo gasto pelo ciclista brasileiro para
ultrapassar o ciclista inglês e ganhar a corrida.
a) 1 s.
b) 2 s.
c) 3 s.
d) 4 s.
e) 5 s.
8. (Unicamp 2010) A Copa do Mundo é o segundo maior evento desportivo do mundo, ficando atrás apenas dos
Jogos Olímpicos. Uma das regras do futebol que gera polêmica com certa frequência é a do impedimento. Para que
o atacante A não esteja em impedimento, deve haver ao menos dois jogadores adversários a sua frente, G e Z, no
exato instante em que o jogador L lança a bola para A (ver figura). Considere que somente os jogadores G e Z
estejam à frente de A e que somente A e Z se deslocam nas situações descritas a seguir.
a) Suponha que a distância entre A e Z seja de 12 m. Se A parte do repouso em direção ao gol com aceleração de
3,0 m/s2 e Z também parte do repouso com a mesma aceleração no sentido oposto, quanto tempo o jogador L tem
para lançar a bola depois da partida de A antes que A encontre Z?
b) O árbitro demora 0,1 s entre o momento em que vê o lançamento de L e o momento em que determina as
posições dos jogadores A e Z. Considere agora que A e Z movem-se a velocidades constantes de 6,0 m/s, como
indica a figura. Qual é a distância mínima entre A e Z no momento do lançamento para que o árbitro decida de
forma inequívoca que A não está impedido?
Gabarito
1: a) d = 9920 m b) a = 1,5 m/s²
2: [E]
3: Construindo o gráfico da velocidade em função do tempo para os 10 segundos:
v = 15 m/s
a = 2,25 m/s²
4: a) aB = 0,2 m/s²
5: [D]
6: [D]
7: [E]
t1 = 20/3 s
b) dA = 125 m vA = 2,5 m/s
t2 = 10/3 s
A figura abaixo ilustra a situação descrita. (instante t = 0).
8: a) t = 2 s; b) Dmin 1,2 m.