Volume de sólidos de Revolução - Engenharia Fácil

www.engenhariafacil.weebly.com
Resumo com exercícios resolvidos do assunto:
Aplicações da Integral
(I)
(II)
(III)
Área
Volume de sólidos de Revolução
Comprimento de Arco
(I)
Área
Dada uma função positiva f(x), a área A entre o gráfico de f e o eixo x e as retas
x=a e x=b é dada por:
𝑏
𝐴=
𝑓 𝑥 𝑑𝑥
𝑎
Generalizando, suponha que tem-se duas funções, e que 𝐹(𝑥) ≥ 𝑔(𝑥), ∀ 𝑥 ∈ 𝑎, 𝑏 .
A área A entre o gráfico de g e as retas verticais x=a e x=b é dada por:
𝑏
𝐴=
𝑓 𝑥 − 𝑔 𝑥 𝑑𝑥
𝑎
Sendo f(x) a função que está por cima durante o intervalo [a,b] e g(x) a função que está embaixo.
Exemplo 1: Calcule a área entre os gráficos das funções y=x² e y =2x-x².
Resposta:
Note que o enunciado não nos dá o intervalo, logo temos que a área entre os gráficos é
justamente a área gerada por duas interseções seguidas, logo,vamos resolver por passos para
você se habituar com a resolução destes tipo de questões.
 Passo 1: Encontrar os pontos de interseção,achando a solução ao igualar uma das
componentes das funções (neste caso o y).
𝑦 = 𝑥 = 2𝑥 − 𝑥²
2𝑥² = 2𝑥, 𝑙𝑜𝑔𝑜 𝑥 = 0 𝑜𝑢 𝑥 = 1
 Passo 2: Encontrar qual função é maior entre os dois pontos de interseção,
substituindo valores na função entre os dois pontos (Neste caso, um valor possível
seria x=1/2 pois está entre 0 e 1).
1
𝑥=
2
1
1
𝑓 𝑥 = 𝑦=
²=
2
4
1
1
3
𝑔 𝑥 = 𝑦 = 2. −
²=
2
2
4
2
2
Logo, 𝑔 𝑥 = 2𝑥 − 𝑥 ≥ 𝑓 𝑥 = 𝑥 𝑛𝑜 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑜 0,1
 Passo 3: Integrar as funções de acordo com a definição dada anteriormente para
encontrar a área.
1
1
1
𝐴=
2𝑥 − 𝑥 2 − 𝑥 2 𝑑𝑥 = (2𝑥 − 2𝑥²)𝑑𝑥 =
3
0
0
Dependendo da situação, pode ser melhor integrar com relação ao eixo y.
Exemplo 2:Encontre a área delimitada pelo gráfico das curvas 𝑦² = 2𝑥 + 6 𝑒 𝑦 = 𝑥 − 1.
Resposta:
→Percebe-se que é mais vantajoso integral a curva y²=2x+6 com relação ao eixo y(se
fossemos isolar o y,encontraríamos uma raiz quadrada,que é mais trabalhoso do que
um polinômio normal) ,então, a curva y=x-1 também deve ser integrada a esse mesmo
eixo.
 Passo 1: Alterar as equações de y(x) para x(y) isolando o x ,e encontrar os pontos de
interseção em y.
𝑦²
𝑦² = 2𝑥 + 6 , 𝑖𝑠𝑜𝑙𝑎𝑛𝑑𝑜 𝑜 𝑥, 𝑡𝑒𝑚𝑜𝑠: 𝑥 =
−3
2
𝑦 = 𝑥 − 1, 𝑖𝑠𝑜𝑙𝑎𝑛𝑑𝑜 𝑜 𝑥, 𝑡𝑒𝑚𝑜𝑠: 𝑥 = 𝑦 + 1
A interseção é dada por:
𝑦2
−3=𝑦+1
2
Logo encontramos as raízes y=4 ou y=-2
 Passo 2:Segue o mesmo procedimento do exemplo anterior.
Temos y=0 um valor intermediário entre [-2,4].
𝑥 𝑦 =
𝑦2
− 3, 𝑥 0 = −3
2
𝑥 𝑦 = 𝑦 + 1, 𝑥 0 = 1
Logo, durante o intervalo [-2,4], é válida a equação 𝑦 + 1 ≥
𝑦2
2
−3
 Passo 3:Integramos( função maior) –( função menor), como no exemplo anterior.
𝟒
𝒚+𝟏 −
−𝟐
𝒚𝟐
−𝟑
𝟐
𝟒
𝒅𝒚 =
−𝟐
Exercícios Recomendados:
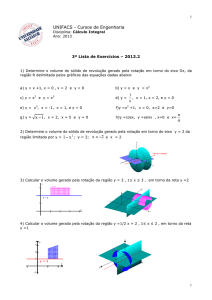
1) (UFRJ-2013.2)
2) (UFRJ-2011.2)
3)
a)
b)
c)
d)
(−
Encontre a área delimitada pelas curvas indicadas:
𝑦 = 12 − 𝑥 2 𝑒 𝑦 = 𝑥 2 − 6
𝑦 = 𝑒𝑥
, 𝑦 = 𝑥𝑒 𝑥
𝑒𝑥=0
2
𝑦 = cos 𝜋𝑥 𝑒 𝑦 = 4𝑥 − 1
𝜋
𝑦 = cos 𝑥
, 𝑦 = 2𝑠𝑒𝑛 𝑥 , 𝑥 = 0 , 𝑥 =
2
𝒚𝟐
+ 𝒚 + 𝟒) 𝒅𝒚
𝟐
(II)
Volume e de sólidos de Revolução
Neste capítulo estudaremos como utilizar integrais para calcular volume de superfícies
planas. Podemos calcular o Volume V, como:
𝑏
𝑉=
𝐴 𝑥 𝑑𝑥
𝑎
Onde A(x) é a área de interseção do sólido com os planos perpendiculares que cruzam
o eixo no ponto x (seção transversal).
No exemplo do cilindro, calculamos 𝑉 =
𝑏
𝑎
𝐴 𝑥 𝑑𝑥 sendo A(x)= Área do círculo
(seção transversal) que é constante durante todo o intervalo [a,b].
Exemplo 1: Calcule o volume da esfera de raio R.
Resposta:
Percebemos que a seção transversal (área de interseção do sólido com o plano perpendicular que cruza o
eixo no ponto x ) é:
Á𝑟𝑒𝑎 = 𝜋𝑦², mas, y = 𝑅² − 𝑥²
Logo, A(x)=𝜋(𝑅 2 − 𝑥 2 )
E o volume pode ser calculado por:
𝑅
𝑉𝑜𝑙𝑢𝑚𝑒 ∶ 𝑉 =
4
𝜋 𝑅 2 − 𝑥 2 𝑑𝑥 = 𝜋𝑅³
3
−𝑅
Sólidos de Revolução
Sólidos de Revolução são sólidos gerados a partir da rotação de uma área
plana A ao redor de um eixo qualquer, como no exemplo abaixo.
A área plana A que temos é uma circunferência, e está sendo rotacionada no eixo y.
Exemplo 1:Encontre o volume do sólido obtido pela rotação em torno do eixo x
da região sob a curva y= 𝑥 ,o eixo x e as retas x=0 e x=1.
Curva y
y rotacionada
Á𝑟𝑒𝑎 = 𝐴(𝑥) = 𝜋𝑅2 = 𝜋𝑦 2 = 𝜋
𝑥
2
= 𝜋𝑥
Para determinar o volume, temos:
1
1
𝐴 𝑥 𝑑𝑥
0
𝜋𝑥𝑑𝑥 =
0
𝜋
2
Sólidos que não são de revolução:
São sólidos como pirâmides, cubos, esferas, entre outros sólidos que não são gerados
por rotação em um eixo.
Exemplo 1: Calcule o volume de uma pirâmide de base quadrada e lado l e altura h.
Resposta:
Utilizando a equação da reta y=ax como uma aresta da face lateral da pirâmide,
podemos desenhar a seguinte figura.
Para encontrarmos o volume desta pirâmide, vamos supor fatias paralelas ao
eixo y com alturas infinitesimais dx:
O volume dessa Área infinitesimal é V=l²dx
Tendo y=l/2 e substituindo na equação anterior, temos:
V=(4y²)dx
A soma dos infinitesimais volumes é dada por:
𝑕
𝑕
4𝑦²𝑑𝑥 = 4
0
𝑥
𝑦²𝑑𝑥 = 4
0
0
𝑆𝑒𝑛𝑑𝑜 𝑎 =
𝑉=
𝑎²𝑥²𝑑𝑥 =
4𝑎2 𝑕3
3
𝑦
𝑙
=
, 𝑡𝑒𝑚𝑜𝑠:
𝑕 2𝑕
4𝑎2 𝑕3 4 𝑙 2
𝑙2 𝑕
=
. 𝑕³ =
3
3 4𝑕²
3
𝑙2 𝑕
𝑉=
3
Cálculo de Volume pelas Cascas Cilíndricas
O método de Cascas Cilíndricas é outra maneira para calcular volumes. Muitas vezes
calcular o volume pelo método anterior não é fácil e algumas vezes nem é possível.
Este método tem o objetivo de calcular o volume de sólidos somando cascas cilíndricas
finas que crescem de dentro pra fora do eixo de revolução.
Seguindo um rápido passo a passo você consegue resolver problemas desse tema:
Temos:
1° Passo: Desenhe a região e esboce um segmento de reta identificando o corte
paralelo ao eixo de rotação. Encontre o raio e altura da casca cilíndrica.
2° Passo: Determine os limites de integração para a variável em questão.
3° Passo: Integre o produto de 2π ⋅ raio ⋅ altura em relação a variável do problema.
A fórmula geral deste método é:
𝑏
𝑉𝑜𝑙𝑢𝑚𝑒 =
2𝜋𝑅𝐹 𝑥 𝑑𝑥
𝑎
Onde o R será o raio da rotação e o F(x) será a altura, isso ficará mais claro nos exemplos.
Exemplo 1:Encontre o volume do sólido obtido ao girar a região delimitada por y = f(x)
= 3x – x² gira em torno da reta x = -1.
Corte uma fatia cilíndrica (paralelamente ao eixo de revolução) na parte interna do
sólido.Depois corte outra fatia em torno do primeiro corte, e assim por diante. Cada
cilindro encontrado terá raio de aproximadamente 1+𝑥𝑘 , altura 3𝑥𝑘 -𝑥𝑘 ² e espessura
dx.
Se desenrolássemos o cilindro em 𝑥𝑘 teriamos uma fatia retangular de espessura dx. O
comprimento da circunferência interna do cilindro será 2π . R = 2 π ( 1+𝑥𝑘 ).Portanto, o
volume do sólido retangular é:
∆V ≈ largura X altura X espessura ≈ 2 𝜋 ( 1 + 𝑥𝑘 ) . ( 3𝑥𝑘 − 𝑥𝑘 ²). 𝑑𝑥
Somando todos os volumes ao longo de todo o intervalo de x obtemos uma soma de
Riemann. Basta então aplicar o limite para dx tendendo a zero e obtemos a integral.
Os limites de integração são as interseções entre as duas curvas dadas(de onde até
onde a será integral), nesse caso y=0 e y= 3x-x², logo os limites são 0 e 3.
Generalizando para x, temos:
𝑏
3
2𝜋𝑅𝐹 𝑥 𝑑𝑥 =
𝑎
2 𝜋 ( 1 + 𝑥 ) . ( 3𝑥 − 𝑥²). 𝑑𝑥
0
Exemplo 2:Encontre o volume do sólido de revolução obtido ao girar a região limitada
por y=x-x² e y=0 em torno da reta x=2.
Temos a seguinte curva:
Vemos que o limite de integração entre y=x-x² e y=0 são 0 e 1.
Fazendo a rotação na reta vertical x=2, temos:
Neste caso , vemos que ao escolher um x arbitrário, o raio da rotação passa a ser 2-x e
a altura a própria função x-x²-0 = x-x², aplicando na fórmula, temos:
1
2𝜋 2 − 𝑥 𝑥 − 𝑥 2 𝑑𝑥
𝑉𝑜𝑙𝑢𝑚𝑒 =
0
Exercícios:
4) (UFRJ-2013.2)
5) (UFRJ-2013.1)
6) (UFRJ-2012.2)
7) (UFRJ-2012.1)
8) (UFRJ-2011.2)
Comprimento de Arco
Vamos supor que uma curva f(x) qualquer seja uma linha. Se esticássemos esta linha e
medíssemos com uma régua, encontraríamos o comprimento desta curva. Para
determinar este comprimento, costumamos (no Cálculo I , apenas) utilizar a seguinte
equação:
𝑏
1 + (𝑓 ′ 𝑥 )²𝑑𝑥
𝐶𝑜𝑚𝑝𝑟𝑖𝑚𝑒𝑛𝑡𝑜 = 𝐿 =
𝑎
Exemplo 1: Calcule o comprimento da parábola x= y² do ponto (0,0) ao ponto (1,1).
Se tentarmos integrar com relação à x a
função seria y= 𝑥 ,e veríamos que não seria
possível esta integração por esta fórmula (essa
fórmula não é valida para qualquer função,veja
qual eixo é melhor para fazer a integral (x ou y)).
Logo, deve-se integrar com relação a y.
F(y) = x= y²
Aplicando na fórmula, temos:
1
1 + 𝐹′ 𝑦
𝐿=
2
𝑑𝑦
0
1
1
1 + 2𝑦 2 𝑑𝑦 =
𝐿=
0
1 + 4𝑦²𝑑𝑦
0
Exercícios:
9)(UFRJ-2013.2)
10)Encontre o comprimento exato das curvas:
3
a)y = 1 + 6x 2
1
b)x = 3 y y − 3
0≤x≤1
1≤x≤9
c)y = ln 1 − x 2
,0 ≤ x ≤ 2
Gabaritos:
, 𝐹 𝑦 = 2𝑦
1
1)a)
b)
1
2
2
𝜋
2) ln3 3)a) 72 b) e-2 c) +
2
2
3
1
2
d)=
𝜋
252
4)
32
=4/3
5)
𝜋 2 −𝜋
6
6)
4𝜋
15
7)2𝜋 8)±
1
𝜋+2
1
9) ln( 3 + 2) 10)a)243 (82 82 − 1) b) 3 c) ln3 − 2
Bons Estudos!!
Dúvidas?
Acesse o Solucionador na página www.engenhariafacil.weebly.com ou mande email para
[email protected] .