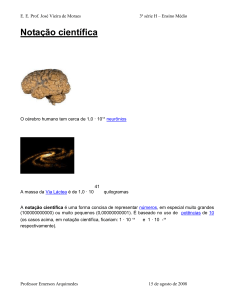
notação científica

Notação científica
NOTAÇÃO CIENTÍFICA
----Notação científica é uma forma breve de representar números, muito grandes
ou muito pequenos, de uma forma mais adequada de trabalhar. Com o auxílio de
potências de base 10.
----Esses números como o próprio nome já explica é usado em anotações
cientificas. Por exemplo, a superfície do sol é de 6,09 × 10¹² km². Imagine o
tempo que levaria para escrever este número. Outro exemplo é a massa real de um
próton que é aproximadamente, 1,6 multiplicados por dez elevado a vinte e
quatro ou 0, 00000000000000000000000000167 gramas.
CONCEITO HISTÓRICO:
----A primeira tentativa conhecida de representar números demasiadamente
extensos foi empreendida pelo matemático e filósofo grego Arquimedes, e descrita
em sua obra O Contador de Areia, no século III a.C.. Ele desenvolveu um método
de representação numérica para estimar quantos grãos de areia existiam no
universo. O número estimado por ele foi de 1 X 1063 grãos.
----Foi através da notação científica que foi concebido o modelo de representação
de números reais através de ponto flutuante. Essa ideia foi proposta
independentemente por Leonardo Torres y Quevedo (1914), Konrad Zuse (1936) e
George Robert Stibitz (1939). A codificação em ponto flutuante dos computadores
atuais é basicamente uma notação científica de base dois.
MODELO:
----A notação cientifica segue um modelo simples, n .10* ela é formada por um
coeficiente, também chamado de mantissa, (n) multiplicado por dez, o qual será
elevado a um expoente(*) correspondente as casas decimais que foram "corridas."
Exemplo: 1000 = 1. 10³
PADRÃO*:
----A definição básica de notação científica permite uma infinidade de
representações para cada valor. Mas a notação científica padronizada inclui uma
restrição o coeficiente deve ser maior ou igual a 1 e menor que 10. Desse modo
cada número é representado de uma única maneira.
*para as notações cientificas padronizadas não em todas.
ESCREVENDO UM NÚMERO EM NOTAÇÃO CIENTÍFICA:
PRIMEIRO: Observe onde se encontra a vírgula caso ela não seja vista,
podemos concluir obviamente que ele se encontra depois da unidade. Por exemplo,
no número 132 a vírgula se encontra depois do 2. (pois 132,0 é igual a 132, já
que os número zero depois da vírgula não tem valor)
SEGUNDO: Como já lemos as notações cientificas costumam ter um
coeficiente maior que 1 e menor que 10, assim continuando o exemplo, o coreto
será andar duas casa decimais para a esquerda assim: 132 = 1,32 x 10², como
você pode perceber, que como "andou-se" duas casas decimais, elevamos o
expoente do numero dez a dois.
--
www.matematicapura.com.br
Notação científica
--Pronto temos uma notação cientifica, Mas isso foi inventado para facilitar a escrita
e também as operações matemáticas com números muito grandes e muito
pequenos. Exemplificando um pouco.
EXEMPLO DE COMO ESCREVER UM NÚMERO EM NOTAÇÃO:
1. A “Cada casa decimal “andada”, diminui-se o valor do coeficiente,
aumentando o expoente em uma unidade, e vice-versa”.
2. Quando o número a ser transformado for maior que um, a vírgula
"andara" para a esquerda, e o expoente será positivo.
3. Quando o número a ser transformado for menos que um, a vírgula
"andara" para a direita e o expoente será negativo.
EXEMPLOS:
a) 12 000 000 000 000 = 1,2 x 10¹³
b) 5 481 = 5, 481x10³
c)255,5 = 2, 555 x 10²
Com números menores que um.
d) 0 0025 = 2,5 x 10 elevado a -3 (2,5x10-3)
e) 0 0458 = 4,58 x 10 elevado a -2 (4,58x10-2)
OPERAÇÕES MATEMÁTICAS COM NOTAÇÕES:
ADIÇÃO E SUBTRAÇÃO:
-----Para somar ou subtrair dois números em notação científica, é necessário que o
expoente seja o mesmo. Ou seja, um dos valores deve ser transformado para que
seu expoente seja igual ao do outro. A transformação segue o mesmo princípio de
equilíbrio. O resultado possivelmente não estará na forma padronizada, sendo
convertido posteriormente.
EXEMPLOS:
a) 4,1 x 107 + 3,5 x 105 = 4,1 x 107 + 0,035 x 107 = 4,135 x 107
b) 6,35 x 109 - 6,25 x 109 = 0,10 x 109 (não padronizado) =10 x 107(padronizado)
www.matematicapura.com.br
Notação científica
Multiplicação:
----Multiplicamos as mantissas e somamos os expoentes de cada valor. O resultado
possivelmente não será padronizado, mas pode ser convertido:
Exemplos:
c) (6,2 x 108) . (3,5 x 105) = (6,2 x 3,5) • 108+5 = 21,8 x 1013
(não padronizado)
= 2,18 x 1014 (padronizado)
d)(4 x 106) x (2,5 x 10-15) = (4 x 2,5) x106+(-15) = 10 x 10-9
DIVISÃO:
----Divide-se os coeficiente e subtraímos os expoentes de cada valor. O resultado
possivelmente não será padronizado, mas pode ser convertido:
EXEMPLOS:
e)(8 x 1017) / (2 x 109) = (8 :2) x 1017-9 = 4 x 108 (padronizado)
f)(2,4 x 10-7) / (6,2 x 10-11) = (2,4 / 6,2) x 10-7-(-11) ≈ 0,3871 x 104
(não padronizado)
= 3,871 x 10³ (padronizado)
EXPONENCIAÇÃO:
----A mantissa é elevada ao expoente externo e o expoente da base dez é
multiplicado pelo expoente externo.
g)(2 x 106)4 = (24) x 106 x 4 = 16 x 1024 = 1,6 x 1025 (padronizado)
RADICIAÇÃO:
----Antes de fazer a radiciação é preciso transformar um expoente para um valor
múltiplo do índice. Depois de feito isso, o resultado é a radiciação da mantissa
multiplicada por dez elevado à razão entre o expoente e o índice do radical.
www.matematicapura.com.br