questão 16 - Colégio OBJETIVO

Nome: _________________________________________
____________________________ N.º: __________
endereço: ______________________________________________________________ data: __________
Telefone:_________________ E-mail: _________________________________________________________
PARA QUEM CURSA O 9.O ANO DO ENSINO FUNDAMENTAL EM 2016
Colégio
Disciplina:
Prova:
MaTeMÁTiCa
desafio
nota:
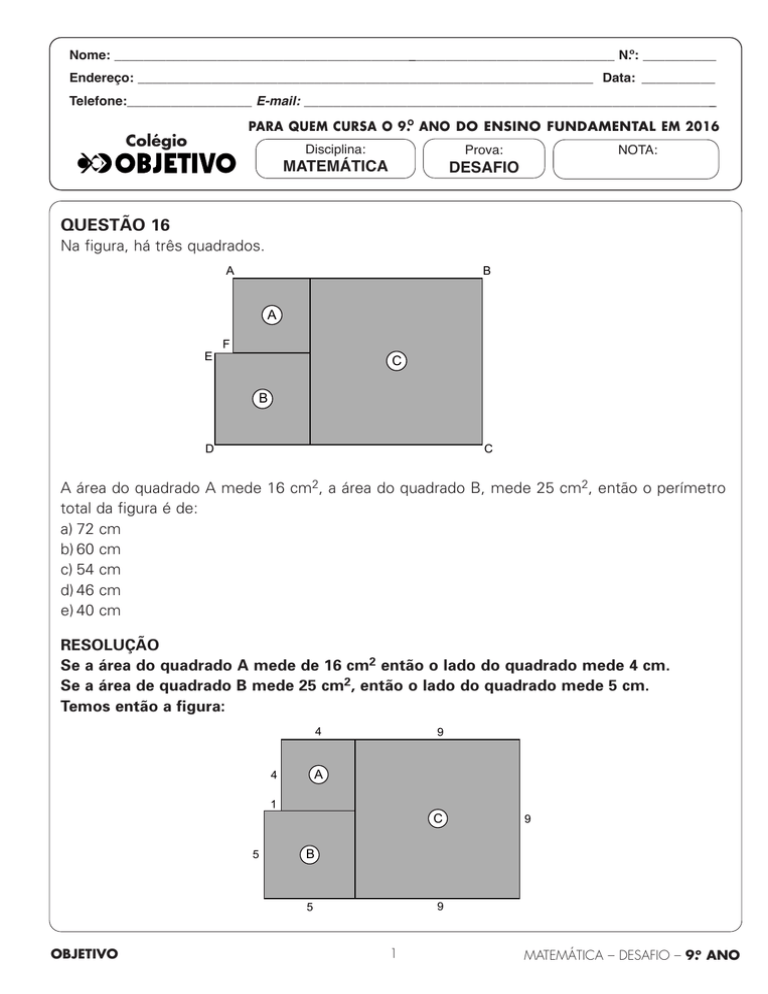
QUESTÃO 16
Na figura, há três quadrados.
A
B
A
E
F
C
B
D
C
A área do quadrado A mede 16 cm2, a área do quadrado B, mede 25 cm2, então o perímetro
total da figura é de:
a) 72 cm
b) 60 cm
c) 54 cm
d) 46 cm
e) 40 cm
RESOLUÇÃO
Se a área do quadrado A mede de 16 cm2 então o lado do quadrado mede 4 cm.
Se a área de quadrado B mede 25 cm2, então o lado do quadrado mede 5 cm.
Temos então a figura:
4
9
A
4
1
5
C
B
9
5
OBJETIVO
9
1
MATEMÁTICA – DESAFIO – 9.o ANO
Assim o perímetro total da figura é igual a
2 . 4 + 2 . 5 + 3 . 9 + 1 = 8 + 10 + 27 + 1 = 46 cm
Resposta: D
QUESTÃO 17
(UNICAMP) – Uma empresa tem 5000 funcionários. Desses, 48% têm mais de 30 anos,
36% são especializados e 1400 têm mais de 30 anos e são especializados. Se x é o número
de funcionários que têm até 30 anos e não são especializados, então:
a) 2200 < x < 2500
b) 2300 ≤ x < 2600
c) 2200 ≤ x < 2600
d) 2000 ≤ x < 2200
e) 2300 ≤ x ≤ 2500
RESOLUÇÃO
Mais de 30 anos
1000
Especializados
1400
400
2200
Funcionários com mais de 30 anos:
48% de 5000 = 2400
Funcionários especializados:
36% de 5000 = 1800
Funcionários com maisM de 30 anos e especializados = 1400
Funcionários que têm até 30 anos e não são especializados:
5000 – 1000 – 1400 – 400 = 2200
Especializados
Não especializados
Mais de
30 anos
1400
1000
Até
30 anos
400
2200
Resposta: C
OBJETIVO
2
MATEMÁTICA – DESAFIO – 9.o ANO
QUESTÃO 18
(0,1) . (0,001) . 10–1
(VUNESP) – Se x = 10–3, então ––––––––––––––––––– é igual a:
10 . (0,0001)
a) 100x
b) 10x
c) x
x
d) ––
10
x
e) –––
100
RESOLUÇÃO
Resolvendo a expressão, utilizando as potências de base dez, temos:
(0,1) . (0,001) . 10–1
10–1 . 10–3 . 10–1
10–5
––––––––––––––––––– = ––––––––––––––––––
= –––––
= 10–2 = 10 . 10–3 = 10 . x, pois
10 . (0,0001)
10 . 10–4
10–3
x = 10–3
Resposta: B
QUESTÃO 19
–––
–––
–––
–––
(FUVEST) – Na figura abaixo, têm-se AC = 3, AB = 4 e CB = 6. O valor de CD é:
A
C
D
B
29
a) –––
12
25
b) –––
12
23
c) –––
12
19
d) –––
12
17
e) –––
12
OBJETIVO
3
MATEMÁTICA – DESAFIO – 9.o ANO
RESOLUÇÃO
A
3
C
x
4
h
6-x
D
B
6
–––
–––
Se h é a altura do triângulo ACB relativa ao lado CB, e se x é a medida de CD, então:
1) No triângulo ADC, tem-se:
h2 + x2 = 33  h2 + x2 = 9
2) No triângulo ADB, tem-se:
h2 + (6 – x)2 = 42
h2 + x2
29
– 12x + 36 = 16  9 – 12x + 36 = 16  x = –––
12
Resposta: A
QUESTÃO 20
3.
20 + 80 – 2.
45 , encontraremos:
Escrevendo na forma mais simples a fração –––––––––––––––––––
8
a) 0,5.
5
3
b) –––
2
5
c) 0,25.
3.3
d) –––––
4
e) 5.5
RESOLUÇÃO
Simplificando a fração, temos:
20 + 80 – 2 .
45
4 . 5 + 16 .
5 – 2.
9.
5
5 + 4.
5 – 2.3.
5
3.2.
3.
3
––––––––––––––––––– = –––––––––––––––––––––––––––– = ––––––––––––––––––––– =
8
8
8
5 + 45 – 6
5
6
5
4
= –––––––––––––––– = –––––
5
= 0,5.
8
8
Resposta: A
OBJETIVO
4
MATEMÁTICA – DESAFIO – 9.o ANO
QUESTÃO 21
Uma escada de 2,5m de comprimento se apoia num muro vertical do qual seu pé, apoiado
no chão horizontal, dista 70cm. Se o pé da escada for afastado mais 8dm do muro, qual o
deslocamento verificado na extremidade superior da escada?
a) 1m
b) 0,4m
c) 40dm
d) 5dm
e) 0,2m
RESOLUÇÃO
Como 2,5m = 25dm e 70cm = 7dm, temos
1.a situação
2.a situação
x
25
7
25
y
7 + 8 = 15
Aplicando Pitágoras, temos:
1.a situação
252 = x2 + 72
x2 = 625 – 49 = 576  x = 576 = 24, pois x > 0
2.a situação
252 = y2 + 152
y2 = 625 – 225 = 400  y = 400 = 20, pois y > 0
O deslocamento da extremidade superior é x – y = (24 – 20)dm = 4 dm = 0,4m
Resposta: B
OBJETIVO
5
MATEMÁTICA – DESAFIO – 9.o ANO
QUESTÃO 22
(SARESP) – Um espião de guerra enviou ao seu comando a seguinte mensagem:
5n + 25 > 5500
– 8n + 3501 > 210 – 5n
O comando sabia que a letra n representava o número de foguetes do inimigo. Fazendo os
cálculos, o comando descobriu que o número de foguetes era igual a:
a) 1094
b) 1095
c) 1096
d) 1097
e) 1098
RESOLUÇÃO
Resolvendo as inequações temos:
5n + 25 > 5500  5n > 5475  n > 1095
– 8n + 3501 > 210 – 5n  –3n > – 3291  n < 1097
Se n > 1095 e n < 1097 então n = 1096, pois n é inteiro.
Resposta: C
QUESTÃO 23
(UNICAMP) – Ao serem retirados 128 litros de água de uma caixa d’água de forma cúbica, o
nível da água baixa 20cm. A capacidade da caixa é:
a) 5,12 . 103ᐉ
b) 51,2 . 10–1ᐉ
c) 256ᐉ
d) 80ᐉ
e) 5,12 . 102ᐉ
RESOLUÇÃO
20
x
x
x
OBJETIVO
6
MATEMÁTICA – DESAFIO – 9.o ANO
Seja x a medida em centímetros da aresta do cubo.
Como 128ᐉ correspondem a 128000cm3, temos:
x . x . 20 = 128000  x2 = 6400  x = 80, pois x > 0
Assim, o volume V do cubo é:
V = (80cm)3 = 512000cm3 que correspondem a 512ᐉ = 5,12 . 102ᐉ
Resposta: E
QUESTÃO 24
Um campo de futebol de 90 m de largura por 110 m de comprimento foi construído em um
terreno de 120 m de largura por 150 m de comprimento, conforme a figura.
150m
120m
90m
90m
120m
110m
110m
150m
Se a área do campo for aumentanda em 1025 m2, qual será o acréscimo à largura e ao
comprimento do campo de futebol, sabendo que esse acréscimo é o mesmo tanto para a
largura quanto para o comprimento?
a) 9 m
b) 8 m
c) 7 m
d) 6 m
e) 5 m
RESOLUÇÃO
Sendo x, em metros, a medida do acréscimo, temos:
Nova área do campo = área antiga + 1025, em m2
(110 + x) (90 + x) = 110 . 90 + 1025  200x + x2 = 1025  x2 + 200x – 1025 = 0 
– 200 ±
44100
– 200 ±
2002 – 4 . 1 . (– 1025)
 x = ––––––––––––––––––––––––––––––––  x = ––––––––––––––––– 
2
2
– 200 ± 210
 x = –––––––––––  x = 5, pois x é positivo
2
Resposta: E
OBJETIVO
7
MATEMÁTICA – DESAFIO – 9.o ANO
QUESTÃO 25
Qual o resultado da expressão:
3
64 . 2–3
–––––––––––––– = ?
2
2
23 : (23)
a) 2–1
b) 2–5
c) 22
2
d) 22
e) 20
RESOLUÇÃO
Resolvendo a expressão temos:
3
1
2
2 . ––
––
6
64 . 2–3
–3
64 . 2
8
8
1
1
1 = 1 = 2–5
= –––––––
= ––––– = ––– . ––– = –––
–––
–––––––––––––– = ––––––––––
3
9 : 26
8
2
4
8
2
2
32
25
2
23 : (23)
Resposta: B
QUESTÃO 26
11
A expressão algébrica que representa o volume de um cubo de aresta –––– x2y3 é:
10
13,31
a) ––––––– x6y9
10
b) 1,21 x4y6
c) 13,31 x6y6
13,31
d) ––––––– x6y9
100
e) 1,221x4y9
RESOLUÇÃO
11
V = ––– x2y3
10
Resposta: A
OBJETIVO
3
1331
= –––––– (x2)3 . (y3)3 = 1,331x6y9 =
1000
8
13,31 6 9
––––– x y
10
MATEMÁTICA – DESAFIO – 9.o ANO
QUESTÃO 27
Na figura, P, R e S são colineares.
R
10
3Ö41
S
y
x
P
12
Q
Podemos afirmar que:
a) y : x = 2,5
b) x . y = 60
c) x + y = 18
d) y – x = 10
x
e) ––– = – 9
y
RESOLUÇÃO
Os lados do triângulo retângulo RPQ medem:
–––
RP = 10 + x (cateto)
–––
PQ = 12 (cateto)
–––
RQ = 3 41 (hipotenusa)
Aplicando o teorema de Pitágoras temos:
(3
41)2 = (10 + x)2 + 122
369 = 100 + 20x + x2 + 144
x2 + 20x – 125 = 0
– 20 ± 202 – 4 . 1 . (–125)
x = ––––––––––––––––––––––––––
2
–20 + 30
x1 = –––––––––  x1 = 5
2
900
–20 ± x = ––––––––––––
2
–20 – 30
x2 = –––––––––  x2 = – 25
2
OBJETIVO
9
MATEMÁTICA – DESAFIO – 9.o ANO
Assim, x = 5, pois x > 0
Os lados do triângulo retângulo SPQ, medem:
–––
SP = 5 (cateto)
–––
PQ = 12 (cateto)
–––
SQ = y (hipotenusa)
Aplicando o teorema de Pitágoras temos:
y2 = 52 + 122
y2 = 25 + 144
y2 = 169
y = ± 169  y = 13, pois y > 0
Assim x + y = 5 + 13 = 18
Resposta: C
QUESTÃO 28
1
Se a = ––
4
1
e b = ––
2
2
3
, o valor numérico da expressão (a + b) . (a – b) é igual a:
7
a) – ––––
64
5
b) ––––
256
10
c) – ––––
96
3
d) – –––––
256
6
e) ––––
64
RESOLUÇÃO
(a + b) . (a – b) = a2 – b2
1
1 2
a = –– = –––
16
4
1
b = ––
2
3
1
= –––
8
1
então: –––
16
2
1
– ––
8
2
1
1
1–4
3
= ––– – ––– = –––––– = – –––
256 64
256
256
Resposta: D
OBJETIVO
10
MATEMÁTICA – DESAFIO – 9.o ANO
QUESTÃO 29
O produto dos cinco primeiros números primos positivos é igual a:
a) 210
b) 4620
c) 1155
d) 2310
e) 1501
RESOLUÇÃO
Os primeiros cinco números primos são 2, 3, 5, 7 e 11. O produto desses números é
igual a:
2 . 3 . 5. 7 . 11 = 2310
Resposta: D
QUESTÃO 30
Observe as frações representadas nas figuras A, B e C, pela parte escurecida em relação ao
todo.
Podemos afirmar que a soma das frações representadas por A, B e C é igual a:
13
a) –––
10
17
b) –––
20
c) 1
19
d) –––
20
9
e) –––
10
OBJETIVO
11
MATEMÁTICA – DESAFIO – 9.o ANO
RESOLUÇÃO
1
1
2
As frações representadas são: A = –– ; B = –– e C = ––
2
4
10
A soma das frações representadas por A, B e C é:
1
1
2
10 + 5 + 4
19
–– + –– + –– = –––––––––– = ––
2
4
10
20
20
Resposta: D
OBJETIVO
12
MATEMÁTICA – DESAFIO – 9.o ANO