Preferência Revelada - Instituto de Economia

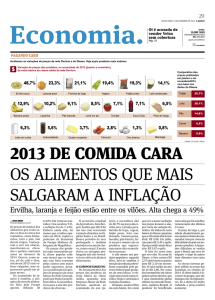
Preferência Revelada
A teoria da escolha a partir das preferências do consumidor tem uma
característica interessante que é sua subjetividade. Dessa maneira, não é algo
observável. No entanto, a escolha, em si, é algo que o analista econômico pode
observar. Surge, então, a possibilidade de se montar uma teoria a partir de algo
que é intrinsecamente observável, ou seja, a escolha. A partir da observação da
escolha e de pequenos requisitos sobre a racionalidade do indivíduo, Samuelson
elaborou uma teoria que permite chegar a conclusões muito próximas àquelas
chegadas pela teoria baseada na existência de um conjunto de preferências
subjetivamente determinadas.
A seguir, procuramos apresentar alguns elementos dessa teoria.
Suponha um conjunto de cestas X, tal que:
{
}
X = ℜ n+ = x ∈ ℜ n : xi ≥ 0, i = 1,..., n
 x1 
 
x=M 
x 
 n
A estrutura de escolha (Ɓ, C(.)) é composta por dois ingredientes:
(i) Uma família Ɓ de subconjuntos de X,B ⊂ X , tal que B є Ɓ, sendo B, por
conveniência, definido como conjunto orçamentário. Os subconjuntos B є Ɓ
são experimentos realizados;
(ii) C(.) é uma regra de escolha que designa um subconjunto C(B) contido em B
de elementos escolhidos para B є Ɓ.
Hipóteses adicionais sobre o conjunto B:
(i) Bens são trocados em mercados competitivos (indivíduo não afeta o preço)
aos preços p, sendo pi>0 para todo i;
(ii) Existe uma renda m à disposição do consumidor.
B p ,m = {x ∈ ℜ; p.x ≤ m}
Hipóteses sobre C(B), o conjunto de escolha:
(i) O conjunto de escolha pertence à linha orçamentária, ou seja, o consumidor
gasta toda sua renda e não mais do que sua renda. Alguns autores (MasCollel et
al. 1995) denominam essa hipótese de Lei de Walras (obs: a lei de Walras afirma
que os excessos de demanda se igualam a 0);
(ii) O conjunto de escolha contém apenas um componente;
(iii) A escolha atende à característica de ser homogênea de grau zero em preços e
renda, ou seja: x(p, m ) = x(αp, αm )
A essas hipóteses deve-se adicionar o axioma fraco da preferência revelada (AFrPR):
A estrutura de escolha (Β, C ( B ) ) satisfaz o axioma fraco da preferência revelada se,
para todo B ∈ Β com x e y ∈ B e x ∈ C ( B ), então, para B'∈ Β, com x e y ∈ B ' , y ∉ C ( B ' ).
Afirmamos, então, que o consumidor revelou diretamente sua preferência por x em
relação a y. x≿y
Isto significa afirmar que se x é escolhido quando y estava disponível, então, y não
poderá ser escolhido se x estiver disponível.
A partir dessas hipóteses, podemos extrair várias propriedades da demanda marshalliana tendo
como único requisito de racionalidade o atendimento ao axioma fraco da preferência revelada.
O gráfico 1 apresenta a curva renda-consumo (caminho de expansão da renda) para bens
inferiores. Reparem que, sob quaisquer escolhas, aceitamos as hipóteses 1 a 3 sobre o conjunto
de escolha, e ocorre o atendimento ao AFrPR. O gráfico 2 apresenta a curva preço-consumo
que também atende aos pressupostos levantados acima.
x2
x2
Curva renda-consumo
Curva preço-consumo
x1
Gráfico 1
Gráfico 2
x1
O atendimento à lei da demanda compensada impede, no entanto, que, uma vez tendo optado
pela cesta x na restrição Bp,m, o consumidor venha optar pela cesta y na restrição Bp’,m’, porque a
restrição x continua disponível na restrição Bp’,m’ e y estava disponível quando x foi escolhida.
Quando o processo de escolha de um consumidor atende a testes como esse, afirmamos que o
consumidor passou no teste do axioma fraco da preferência revelada.
MasCollel et al. (1995:12-14) mostram que, se o consumidor atende o requisito de
racionalidade a partir da teoria das preferências subjetivas, ou seja, às hipóteses de
preferências completas e transitivas, ele obrigatoriamente passará no teste do axioma fraco da
preferência revelada. Contudo, o inverso só será verdadeiro se o consumidor se confrontar com
todas as escolhas possíveis duas a duas e passar no teste. Nesse sentido, as hipóteses de
preferências completas e transitivas são mais fortes do que o axioma forte da preferência
revelada.
x2
O consumidor atenderá às hipóteses de
preferências completas e transitivas se passar
x
no teste do axioma forte da preferência
revelada. O axioma forte da preferência
revelada exige que se x for revelada preferível
a y e y for revelada preferível a z, então x
também será revelada preferível a z, ou seja,
será indiretamente revelada preferível,
enquanto o axioma fraco só implica a revelação
B p ,m
y B p ',m'
direta de preferência.
x1
Gráfico 3
Lei da Demanda Compensada
Se a demanda marshalliana, x(p,m) é homogênea de grau zero em preços e renda e atende a lei de
Walras, então, o axioma fraco da preferência revelada implica a lei da demanda compensada:
(p’-p)(x(p’,m’)-x(p,m))≤0 (1),
em que m’=p’.x(p,m) (2).
Graficamente, o ajuste da renda m’ é representado por
uma linha orçamentária que passa pela cesta inicial
x(p,m) e que tem sua inclinação definida por p’, como
observado no gráfico 4 pela restrição Bp’,m’.
x2
x
B p ,m
B p ',m '
x1
Gráfico 4
O gráfico 4 também ajuda a compreender a afirmação.
Suponha que o consumidor tenha escolhido a cesta x
quando a restrição era Bp,m. Com a mudança de preços
relativos provocada pelo vetor p’ e a compensação da
renda, gera-se uma nova restrição definida por Bp’,m’.
Pela lei de Walras sabe-se que a escolha do consumidor
na nova restrição estará sobre a linha orçamentária. Ao
mesmo tempo, sabe-se que qualquer ponto da nova
linha orçamentária em sua parte tracejada (à direita de
x) não poderá ser escolhido dado o AFrPR, ou seja,
dado que essas cestas estavam disponíveis quando x foi
escolhida. Assim, a escolha ou será x ou será uma cesta
situada na parte contínua da nova linha orçamentária.
Note-se que, na parte contínua, a quantidade do bem 1 é menor do que a quantidade
anteriormente escolhida para o bem 1 e que a quantidade do bem 2 é maior do que a quantidade
anteriormente escolhida para o bem 1. Por sua vez, os preços relativos indicam que o preço do
bem 1 é maior do que o preço anterior do bem 1, sendo o inverso verdadeiro para o bem 2, o
que confirma a lei de demanda compensada. Mais formalmente, a partir de (1):
p'.(x(p' , m' ) − x(p, m) ) − p.(x(p' , m' ) − x(p, m) ) ≤ 0 (3)
Sabe - se que o primeiro termo da equação (3) é igual a 0, pela regra de compensação (2). Logo :
− p.(x(p' , m' ) − x(p, m) ) ≤ 0 (4)
No entanto, sabe - se que se a cesta x(p' , m' ) pudesse ter sido escolhida quando x(p, m) foi
escolhida, ou seja, com a renda p. x(p, m), então, a sua escolha quando a renda fosse
p'. x(p, m) violaria o AFrPR, pois a cesta x(p, m) pode ser consumida com essa nova renda. Logo,
p.x(p' , m' ) > p.x(p, m).
Índices de Preços
Repare que, pela regra de ajuste da renda adotada em (2), adotamos a cesta inicial x(p,m) como
um elemento comum nas duas restrições orçamentárias expostas no gráfico 4. Isso significa que
adotamos essa cesta como um peso comum para a formação da renda. Trata-se de um ajuste da
renda que assegura que o consumidor poderá consumir exatamente a mesma cesta que consumia
antes. Esse critério pode encontrar um paralelo com aquele adotado na compensação hicksiana. A
compensação hicksiana, ao assegurar que a cesta escolhida aos novos preços atenderá o requisito
de que u(x)≤u(y) garante que o consumidor estará pelo menos tão bem quanto antes. Da mesma
maneira, a compensação da renda adotada pelo critério da equação (2) que denominaremos de
compensação de Slutsky, ao garantir que a cesta inicial continua disponível aos novos preços
também assegura que o consumidor estará tão bem quanto antes. No entanto, ao contrário do
critério de Hicks em que o nível de utilidade e sua respectiva curva de indiferença não são
observáveis, a compensação de Slutsky parte da cesta inicial, ou seja, um critério observável. Esse
critério é utilizado para compor índices de preço.
Esse critério pode ser adotado para elaboração de índices de preços. O índice de preços de
Laspèyres adota a cesta inicialmente consumida para a composição do índice:
Lp =
p1 ' x1 + p2 ' x2 + ... + pn ' xn
p1 x1 + p2 x2 + ... + pn xn
(5)
Dessa maneira, o uso de índice de Laspeyres para o cálculo de variação dos preços adota um
critério de ponderação da importância de cada um dos preços de acordo com a cesta que foi
escolhida inicialmente. Como a cesta que acabou sendo consumida no final também é
conhecida, uma forma alternativa de cálculo de variação dos preços é utilizar essa cesta final
como referência. Este critério é conhecido como Paasche:
Pp =
p1 ' x1 '+ p2 ' x2 '+... + pn ' xn '
(6)
p1 x1 '+ p2 x2 '+... + pn xn '
A importância dos índices de preços está na resposta à necessidade de análise de variações de
elementos heterogêneos. Como comparar a importância da variação dos preços de bananas e
maçãs, como contabilizar por isso?
O índice de preços ao consumidor amplo (IPCA-15), utilizado no regime de metas de inflação, é
um índice de Laspeyres que tem como referência a cesta de consumo de famílias que recebem
até 15 a partir da Pesquisa de Orçamento Familiar que teve sua última versão coletada em
2009 e divulgada ano passado. A divulgação da nova cesta implicou uma correção nos cálculos
de inflação.
Já o deflator implícito do PIB que permite calcular taxas de crescimento da economia adota o
critério de Paasche.
Assim como se faz ponderação para se calcular a variação de preços, também pode
ser feita a ponderação para se calcular a variação de quantidades. Esses índices são
denominados de índices de quantidade. Nesse caso, fica-se uma estrutura de preços
de determinado momento e analisa-se a variação da quantidade.
Lq =
p1 x1 '+ p2 x2 '+... + pn xn '
p1 x1 + p2 x2 + ... + pn xn
(7 )
Pq =
p1 ' x1 '+ p2 ' x2 '+... + pn ' xn '
p1 ' x1 + p2 ' x2 + ... + pn ' xn
(8)