Dinâmica - Trabalho, Energia

Física
Fascículo 03
Eliana S. de Souza Braga
Índice
Dinâmica - Trabalho, Energia e Potência
Resumo Teórico ..............................................................................................................................1
Exercícios............................................................................................................................................2
Gabarito.............................................................................................................................................4
Dinâmica - Trabalho, Energia e Potência
Resumo Teórico
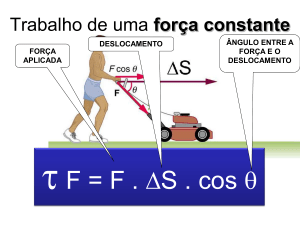
Trabalho de uma força constante
F
θ
τ = F . d . cosθ
d
F
d
τ = F .d
cos 0º = 1
F
cos 90º = 0
τ=0
cos 180º = –1
τ = – F .d
.
F
d
180º
d
Trabalho de uma força de direção constante e módulo variável
F
N
A
τ= Área
d
Teorema da Energia Cinética (T.E.C.)
τFres = ∆Ec = Ecfinal – Ecinicial
Ec =
m.v 2
2
Trabalho da Força Peso
τP = P ⋅ (hi – hf)
Energia Potencial Gravitacional
Epg = P.h = m.g.h
Trabalho da Força Elástica
k
τ Fel = (x i 2 − x f 2 )
2
Energia Potencial Elástica
Epel =
k.x 2
2
1
Potência média
Pot m =
τ
= F.v m .cosθ
∆t
Potência Instantânea
Poti = F.v.cosθ
Rendimento
η=
Pot útil
Pot total
Pottotal = Potútil + Potdissipada
Energia Mecânica
Emec = Ec + Ep
Trabalho realizado pelas forças dissipativas
τFdiss = Emecfinal – Emecinicial
Exercícios
01. (FUVEST-98-1.a FASE) Uma esteira rolante transporta 15 caixas de bebida por minuto, de um depósito
no subsolo até o andar térreo. A esteira tem comprimento 12 m, inclinação de 30º com a horizontal e
move-se com velocidade constante. As caixas a serem transportadas já são colocadas com a velocidade
da esteira. Se cada caixa pesa 200 N, o motor que aciona esse mecanismo deve fornecer a potência
de:
a. 20 W
b. 40 W
c. 300 W
d. 600 W
e. 1800 W
02. (VUNESP-99) Para tentar vencer um desnível de 0,5 m entre duas calçadas planas e horizontais,
mostradas na figura, um garoto de 50 kg, brincando com um skate (de massa desprezível),
impulsiona-se até adquirir uma energia cinética de 300 J. Desprezando-se quaisquer atritos e
considerando-se g = 10 m/s², pode-se concluir que, com essa energia:
a. Não conseguirá vencer sequer metade do desnível.
b. Conseguirá vencer somente metade do desnível.
c. Conseguirá ultrapassar metade do desnível, mas não conseguirá vencê-lo totalmente.
d. Não só conseguirá vencer o desnível, como ainda lhe sobrarão pouco menos de 30 J de energia
cinética.
e. Não só conseguirá vencer o desnível, como ainda lhe sobrarão mais de 30 J de energia cinética.
0,5 m
2
03. (Vunesp-2000) Um corpo cai em queda livre, a partir do repouso, sob a ação da gravidade.Se sua
velocidade, depois de perder uma quantidade E de energia potencial gravitacional, é v, podemos
concluir que a massa do corpo é dada por:
a. 2.E.v
b. 2.E/v2
c. 2.E.v2
d. 2.E.v
e. 2.v2/E
04. (FUVEST-2000) Uma pessoa puxa um caixote, com uma força F, ao longo de uma rampa inclinada de
30º com a horizontal, conforme a figura, sendo desprezível o atrito entre o caixote e a rampa. O
caixote, de massa m, desloca-se com velocidade v constante, durante um certo intervalo de tempo ∆t.
Considere as seguintes afirmações:
v
I. O trabalho realizado pela força F é igual a F.v.∆t
II. O trabalho realizado pela força F é igual a m.g.v.∆t/2
III. A energia potencial gravitacional varia de m.g.v.∆t/2
F
30º
Está correto o que se afirma em:
a. III
b. I e II
c. I e III
d. II e III
e. I, II e III
→
05. (FUVEST-99) Um corpo de massa m é lançado com velocidade inicial v 0 na parte horizontal de uma
rampa, como indicado na figura. Ao atingir o ponto A, ele abandona a rampa, com uma velocidade
→
v A (vAx ;vAy), segue uma trajetória que passa pelo ponto de máxima altura B e retorna à rampa no
→
ponto C. Despreze o atrito. Sejam hA , hB e hC as alturas dos pontos A, B e C, respectivamente. v B (vBx ,
→
vBy) a velocidade do corpo no ponto B e v C (vCx , vCy) a velocidade do corpo no ponto C. Considere as
afirmações:
I. v0 = vAx = vB = vCx
II. vAx = vB = vCx
III.
1
1
m vB2 = m.vA2 – m.g.(hB – hA )
2
2
IV.
1
m v02 = m g hB
2
V.
1
m vAy2 = m g ( hB – hA )
2
São corretas as afirmações:
a. todas
b. somente I e II
c. somente II, III e IV
d. somente II, III, IV e V
e. somente II, III e V
3
06. (FUVEST99) Um veículo para competição de aceleração (drag racing) tem massa M = 1100 kg, motor
de potência máxima P = 2,64.106 W (~ 3 500 cavalos) e possui um aerofólio que lhe imprime uma
força aerodinâmica vertical para baixo, Fa, desprezível em baixas velocidades. Tanto em altas quanto
em baixas velocidades, a força vertical que o veículo aplica à pista horizontal está praticamente
concentrada nas rodas motoras traseiras, de 0,40 m de raio. Os coeficientes de atrito estático e
dinâmico, entre os pneus e a pista, são iguais e valem µ = 0,50. Determine:
a. A máxima aceleração do veículo quando sua velocidade é de 120 m/s, (432 km/h), supondo que não
haja escorregamento entre as rodas traseiras e a pista. Despreze a força horizontal de resistência do ar.
b. O mínimo valor da força vertical Fa, aplicada ao veículo pelo aerofólio, nas condições da questão
anterior. Adote g = 10 m/s2.
c. A potência desenvolvida pelo motor no momento da largada, quando: a velocidade angular das rodas
traseiras é ω = 600 rad/s, a velocidade do veículo é desprezível e as rodas estão escorregando
(derrapando) sobre a pista.
Gabarito
01. Alternativa c.
A esteira se move com velocidade constante e, portanto a aceleração é nula, o que faz a força
resultante: ser nula (Primeira lei de Newton ou Princípio da Inércia). Isto nos permite calcular a força
motora que a esteira faz.
F
N
Psen30º
P cos30º
F – P.sen30º = 0
F = P.sen30º
F = 200 . 0,5 = 100 N
Agora se calcula o trabalho que a força F faz, lembrando que
este é dado por:
30º
τ = F.d.cos0º
τ = 100.12 = 1200 J para cada caixa
Como são 15 caixas por minuto o trabalho total é: τt = 1200.15 = 18 000 J
Potência = trabalho/tempo
P=
e tempo = 1 min = 60 s
18000
= 300W
60
Dica:
A esteira se move com velocidade constante e, portanto a aceleração é nula, o que faz a força
resultante ser nula (Primeira lei de Newton ou Princípio da Inércia). Isto nos permite calcular a força
motora que a esteira faz. Agora se calcula o trabalho que a força F faz, lembrando que este é dado
τ
por τ = F.d.cos0º. Por último, deve-se lembrar que potência = trabalho sobre o tempo P = . (τ em
∆t
joules e ∆t em segundos).
02. Alternativa e.
Adotando-se como referencial, para Epg = 0, o plano mais baixo da trajetória, a energia necessária
para o garoto conseguir vencer o desnível é dada por:
Eg = m.g.h
4
→
Eg = 50.10.0,5
→
Eg = 250 J
Como o sistema é conservativo (não há atritos) e o garoto havia adquirido 300 J de energia cinética,
ele consegue vencer o desnível e ainda lhe sobram Ec = 300 – 250 = 50 J de energia cinética que não
foram transformadas em energia potencial gravitacional.
03. Alternativa b.
O sistema é conservativo e por isso a energia potencial gravitacional perdida pelo corpo, E, é
totalmente transformada em energia cinética:
E=
m.v 2
2
m=
2E
v2
04. Alternativa e.
τ
,
∆t
τ = F.v.cos0º é o trabalho realizado pela força F no intervalo de
tempo ∆t.
I. Correta. A potência da força F é: Pot = F.v.cos 0º =
v
N
30º
F
II. Correta. Como o movimento é uniforme a variação da energia
cinética é nula e, portanto o trabalho resultante é nulo.(Teorema da
Energia Cinética)
P
τF + τP + τN = 0
τF = –τP
τF = – (–m.g.∆h)
v.∆t
sen 30º =
∆h
30º
τF + τP + 0 = 0
∆h
v. ∆t
∆h =
v. ∆t
2
III. Correta. ∆Epot = m.g.∆h = m.g.v.
τF = m.g.v.
∆t
2
∆t
2
05. Alternativa e.
Lembrando que:
v2 = vx2 + vy2
• No ponto B, vBy = 0 e vB = vBx
• Como não há atrito: (EC + EP)0 = (EC + EP)A = (EC + EP)B = (EC + EP)C
• Como no trecho ABC o corpo está sujeito à ação exclusiva do seu peso (vertical), não há aceleração
horizontal e portanto a componente horizontal da velocidade é constante : vAx = vB = vCx .
I. Errado: Como (EC + EP)0 = (EC + EP)A temos 0 + (1/2) m.v02 = m.g.hA + (1/2)m.vA2
vA< v0 e vAx2 = vA2 – vAy2 conclui-se que: vAx < vA < v0
II. Certo: No trecho ABC o corpo está sujeito apenas à ação de seu próprio peso, não havendo
aceleração horizontal não há variação da velocidade horizontal.
III. Certo: (EC + EP)A = (EC + EP)B
1
1
m.vA2 + m.g.hA = m.vB2 + m.g.hB
2
2
1
1
m.vA2 + m.g.hA – m.g.hB = m.vB2
2
2
1
1
m.vB2 = m.vA2 + m.g.(hA – hB)
2
2
5
1
1
m.vB2 = m.vA2 + m.g.{– (–hA + hB)}
2
2
1
1
m.vB2 = m.vA2 – m.g.(hB – hA)
2
2
IV. Errado: (Ec + Ep)0 = (Ec + Ep)B
1
1
m.v02 = m.vB2 + m.g.hB
2
2
V. Certo: (Ec + Ep)A = (Ec + Ep)B
1
1
mvA2 + mghA = mvB2 + mghB
2
2
1
m(vA2 – vB2) = mg(hB – hA)
2
Como vB = vAx
1
m(vA2 – vAx2 ) = mg(hB – hA)
2
Como vA2 = vAx2 + vAy2
1
mvAy2 = mg(hB – hA)
2
06.
a. Supondo que a potência seja máxima, temos:
Potmáx = Fmáx . v
2,64.106 = Fmáx.120
Fmáx = 2,2.104 N
Desprezando a componente horizontal da força de resistência do ar, Fmáx = Fres
2,2.104 = m.a
2,2.104 =1100.a
a = 20 m/s2
b. A força que acelera o veículo é a força de atrito estático entre o chão e a roda de tração:
Fmáx ≤ Fatdestaque
N
4
2,2.10 ≤ µ .(P + Fa)
4
Fa
4
2,2.10 ≤ 0,50 (1,1.10 + Fa)
2,210
. 4
≤ 1,1.104 +Fa
0,50
4,4.104 – 1,1.104 ≤ Fa
P
Fa ≥ 3,3.104 N ∴ o mínimo valor de Fa é 3,3.104 N
c. Com as rodas derrapando o atrito é dinâmico:
Fat = µ .N = µ .P = 0,50.1100.10
Fat = 5 500 N
v = ω .R
v = 600. 0,40
v = 240 m/s
Pot = F. v
Pot = 5500.240
Pot = 1,32.106 W
6