Leis de Kirchoff e sua Aplicação na Análise de Circuitos

2
Matéria
1
Teoria dos Circuitos e Fundamentos de Electrónica
Leis de Kirchoff e sua Aplicação
na Análise de Circuitos
Lei de Kirchhoff das correntes
Lei de Kirchhoff das tensões
Teresa Mendes de Almeida
[email protected]
© T.M.Almeida
ACElectrónica
Fevereiro de 2011
3
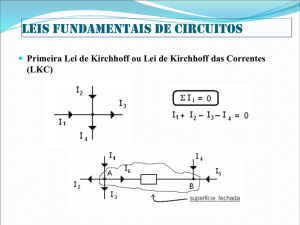
A soma das correntes que entram num nó é igual à soma das
correntes que saem desse nó
e
e
4
i2 + i5 = i4 + i7
sair
equações matematicamente equivalentes
0 = −i2 + i4 − i5 + i7
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
então há outra formulação possível para KCL:
Num nó, a soma algébrica das correntes é nula
∑ ±i
k
=0
k
é preciso arbitrar um sentido para a corrente em cada ramo
e escrever equações KCL concordantes com os sentidos escolhidos
IST-DEEC-ACElectrónica
Fevereiro de 2011
+i2 − i4 + i5 − i7 = 0
s
E quando as correntes não têm um sentido já marcado?...
© T.M.Almeida
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
entrar
baseia-se na conservação da carga eléctrica
também se chama Lei dos Nós
equação tem tantos termos quantos os ramos que ligam ao nó
Nó 3
s
Nó 1
Nó 2
Nó 3
Nó 4 … Nó 5 …
IST-DEEC-ACElectrónica
Lei de Kirchhoff das correntes (KCL)
i1 = i2 + i3
i4 = i1 + i6
i2 + i5 = i4 + i7
Divisor de Tensão
Divisor de Corrente
Análise e simplificação de circuitos
© T.M.Almeida
∑i = ∑i
Resistências em série
Resistências em paralelo
Simplificação de resistências
IST-DEEC-
Lei de Kirchhoff das correntes (KCL)
KVL – lei das malhas
Ligação de componentes em série e em paralelo
Resistências em série e em paralelo
DEEC
Área Científica de Electrónica
KCL – lei dos nós
Generalização de KCL
Fevereiro de 2011
é preciso associar sinal algébrico (+/-) com sentido das correntes
correntes que entram são (+) e correntes que saem são (-)
ou
correntes que entram são (-) e correntes que saem são (+)
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
2
hipóteses
Fevereiro de 2011
5
Quantas equações KCL?
Num circuito com N nós
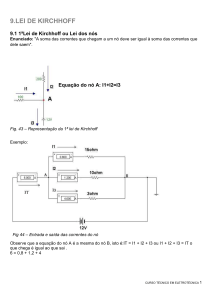
30 + 20 = I5
60 + I5 = I4 + 40
I6 + 40 = 30
I4 = I1 + I6
© T.M.Almeida
IST-DEEC-ACElectrónica
I1 = 80 mA
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Quantos nós?
Quanto vale IT?
Quantas eq. KCL diferentes?
Calcular I1 e I2
Fevereiro de 2011
7
Fevereiro de 2011
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Fevereiro de 2011
8
∑v
baseia-se na conservação da energia eléctrica
k
é preciso associar sinal algébrico (+/-) com polaridade da tensão
quando se circula na malha
+ quando se encontra primeiro o sinal +
– quando se encontra primeiro o sinal –
k
=0
E quando as grandezas não estão marcadas no circuito?
arbitrar polaridades(sentidos) e escrever equações KVL de acordo com
sentidos que foram arbitrados
Também se chama Lei das Malhas
Sentido horário (abcdefa)
Sentido anti-horário (afedcba)
Basta escrever uma das equações
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
IST-DEEC-ACElectrónica
A soma algébrica das tensões numa malha é zero
IST-DEEC-ACElectrónica
I4 = 70 mA
Lei de Kirchhoff das tensões (KVL)
© T.M.Almeida
20 + 60 + 30 = I4 + 40
© T.M.Almeida
Calcular ix
I1 = 80 mA
I4 foi calculada sem se saber I6
Generalização pode ser muito útil em circuitos mais complexos
I1 = 60 + 20
Superfície 2
I6 = -10 mA
Exemplos de aplicação
I4 = 70 mA
superfície fechada
parte do circuito onde se verifique conservação da carga
conjunto de componentes (que não armazenam carga) interligados
pode ser vista como um nó gigante
Superfície 1
Nó 2
I5 = 50 mA
Nó 5
Por onde começar? Qual a sequência de cálculos?
Há mais do que uma forma de calcular? (sim!)
Nó 3
Pode generalizar-se a lei de Kirchhoff das correntes aplicando-a a
uma superfície fechada
Nó 4
podem escrever-se N equações KCL = uma equação para cada nó
mas apenas N-1 equações é que são linearmente independentes!
a N-ésima equação é redundante (pode obter-se a partir das restantes)
Calcular as correntes desconhecidas I1, I4, I5, I6 usando KCL
6
Generalização KCL
+ VR1 – 5 + VR2 – 15 + VR3 – 30 = 0
+ 30 – VR3 + 15 – VR2 + 5 – VR1 = 0
as 2 equações são equivalentes (×-1)
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Fevereiro de 2011
9
Quantas equações KVL?
Quantas equações KVL se podem escrever?
Malha exterior – abcda
+VR1 + (20 VR1) + VR3 – VS = 0
Malha elementar à esquerda – abda
+VR1 + VR2 – VS = 0
Malha elementar à direita – bcdb
+ (20 VR1) + VR3 – VR2 = 0
Há 2 malhas elementares
© T.M.Almeida
pode obter-se a partir das outras duas!
IST-DEEC-ACElectrónica
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Fevereiro de 2011
11
Exemplos de aplicação
Calcular Vec, Vad e Veb
Calcular Vo
IST-DEEC-ACElectrónica
Fevereiro de 2011
12
têm um nó comum → nó b
passa a mesma corrente nos dois componentes
Iab = Ibc
têm dois nós comuns → nós a e b
queda tensão aos terminais é a mesma
Vab
Ligação série / paralelo?
3I1 − Va + 5 I1 − 12 = 0
I1 = 2mA Vo = 10V

Va = 2 I1
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Fevereiro de 2011
Componentes 1 e 2 ligados em paralelo
© T.M.Almeida
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Componentes 1 e 2 ligados em série
3000 I + ( 2Vo ) + Vo − 12 = 0  I = 2mA


Vo = 1000 I
Vo = 2V
IST-DEEC-ACElectrónica
Ligação em série e em paralelo
Calcular Vbd
pelo ramo da esquerda (gerador de tensão)
Vaf = +Va – Vf = 24 V
KVL circulando pelos componentes do lado direito
+16 – 12 + 4 + 6 + 10 – Vaf =0
Vaf = 24 V
© T.M.Almeida
Vec = + Ve – Vc é a incógnita
KVL circulando no sentido horário
Vec + 4 + 6 = 0
Vec = – 10V
Quanto vale Vaf?
apenas 2 das 3 equações KVL são linearmente independentes
a 3ª equação a ser considerada é redundante
Vae = + Va – Ve é a incógnita
KVL circulando no sentido horário
Vae + 10 – 24 = 0 Vae = 14V
Quanto vale Vec?
10
Como usar KVL para determinar queda de tensão entre dois nós?
Quanto vale Vae?
tantas quantas o número de malhas elementares
as restantes equações são redundantes
Circulando em sentido horário em todas as malhas do circuito…
uma por cada malha do circuito
Quantas equações KVL são linearmente independentes?
Usar KVL p/ determinar d.d.p. entre dois nós
paralelo
© T.M.Almeida
IST-DEEC-ACElectrónica
série
paralelo
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
série
Fevereiro de 2011
13
Resistências em série
Duas resistências em série somam-se
KVL (sentido horário)
R1i + R2i − v = 0 v = ( R1 + R2 ) i
Duas resistências em paralelo
1
1
1
= +
RP R1 R2
RS = R1 + R2
v
= R1 + R2
i
N resistências em série somam-se
GP = G1 + G2
RP =
R1 R2
R1 + R2
KCL no nó superior
io =
RS = R1 + R2 + R3 + … + RN
14
Resistências em paralelo
v
v
+
R1 R2
1
1  i
1
1
io = v  +  o = +
 R1 R2  v R1 R2
RP = R1 // R2
N resistências em paralelo
1
1
1
1
1
= +
+ +… +
RP R1 R2 R3
RN
N resistências
iguais
RP = R1 // R2 // R3 // // RN
RS = N × R
RS é sempre maior do que as resistências da série
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Fevereiro de 2011
15
Simplificação de resistências
1
2
3
4
RP = R / N
N resistências iguais
RP é sempre menor do que as resistências do paralelo
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
A tensão divide-se entre duas resistências em série na proporção
directa do valor das suas resistências
a
KCL
 i = iab = iR1

iab = ibc = iR 2
KVL (abca)
Lei Ohm
i=
IST-DEEC-ACElectrónica
i = iR1 = iR 2
vR1 + vR 2 − v = 0
vR1 = R1i

vR 2 = R2i
v
R1 + R2
vR1 =
RAB=5kΩ
© T.M.Almeida
16
Divisor de Tensão
b
5
RAB=3kΩ
Fevereiro de 2011
RAB=22kΩ
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Fevereiro de 2011
R1=R2 vR1 = vR 2 =
© T.M.Almeida
IST-DEEC-ACElectrónica
v
2
R1i + R2i − v = 0
R1
v
R1 + R2
R1=0
(curto-circuito)
vR 2 =
c
R2
v
R1 + R2
 vR1 = 0

 vR 2 = v
 vR1 = v
R1=+∞ v = 0
 R2
(circuito aberto)
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Fevereiro de 2011
17
Divisor de Corrente
A corrente divide-se entre duas resistências em paralelo na
proporção inversa dos seus valores
a
KCL (nó a) i = i1 + i2
Lei Ohm
R1i1 = R2i2
 v = vab = R1i1

v = vab = R2i2
R
i2 = 1 i1
R2
R2

i1 = R + R i

1
2

R
1
i =
i
 2 R1 + R2
R1=R2 i1 = i2 =
© T.M.Almeida
i
2
IST-DEEC-ACElectrónica
i = i1 +
R1
i1
R2
1
G=
R
R1=0
(curto-circuito)
40 + 80
0.9 = 0.6mA
60 + ( 40 + 80 )
I2 =
60
0.9 = 0.3mA
60 + ( 40 + 80 )
Vo = 80k × I 2 = 24V
Simplificar resistências e usar divisor de tensão
R12 = 60 // ( 80 + 40 ) = 40k Ω
R12
R1=+∞
(circuito aberto)
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
i1 = 0

 i2 = i
V1 = R12 I12 = 40 × 0.9 = 36V
Vo =
Fevereiro de 2011
19
© T.M.Almeida
IST-DEEC-ACElectrónica
80
V1 = 24V
80 + 40
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
20
Exemplos de aplicação
Calcular Vab
Qual a potência fornecida por VS?
Quanto vale VS?
Fevereiro de 2011
Quanto vale IA?
Calcular Io
Quanto vale V1?
identificar nós
Pfonte I = 0W
Pfonte I = V fonte I I fonte I = Veb I eb = 0 ⇒ Veb = 0
I1 =
I12
Calcular VS sabendo que a potência posta
em jogo na fonte de corrente é 0W
Calcular I1, I2 e Vo
Divisor de corrente e Lei de Ohm
G1

i1 = G + G i

1
2

i = G2 i
 2 G1 + G2
Exemplo de aplicação
b
 i1 = i

i2 = 0
18
Exemplo de aplicação
a
marcar corrente IE
KCL nós a e f I E = I ab = I fa = I ef
KVL malha elementar à esquerda (abefa)
18
3I E + Vbe + 2 I E − 18 = 0 I E = A
5
0
marcar corrente ID
33
IE + 3 = ID ID =
A
KCL nó b
b
ID
IE
f
c
e
d
5
KCL nós c e d I D = I bc = I cd = I de
KVL malha elementar à direita (bcdeb)
8 I D + VS + 6 I D + Veb = 0 VS = −14 I D = −92, 4V
0
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Fevereiro de 2011
© T.M.Almeida
IST-DEEC-ACElectrónica
TCFE Leis de Kirchhoff e sua Aplicação na Análise de Circuitos
Fevereiro de 2011