TC DE FÍSICA – 9º ANO – OLIMPÍADA AULAS DE 4 A 7

TC DE FÍSICA – 9º ANO – OLIMPÍADA
Professor: Rodrigo Lins
ALUNO(A):
Nº
TURMA:
TURNO:
DATA:
/
/
COLÉGIO:
OSG 1423/11
AULAS DE 4 A 7
MOVIMENTO RETILÍNEO UNIFORMEMENTE
VARIADO (MRUV)
a = Cte ≠ 0
1. CONDIÇÕES:
∆V é Diretamente Proporcional a ∆t.
2. ACELERAÇÃO ESCALAR MÉDIA (aM)
Aceleração escalar média entre dois instantes é a
variação de velocidade escalar instantânea ocorrida, em
média, por unidade de tempo:
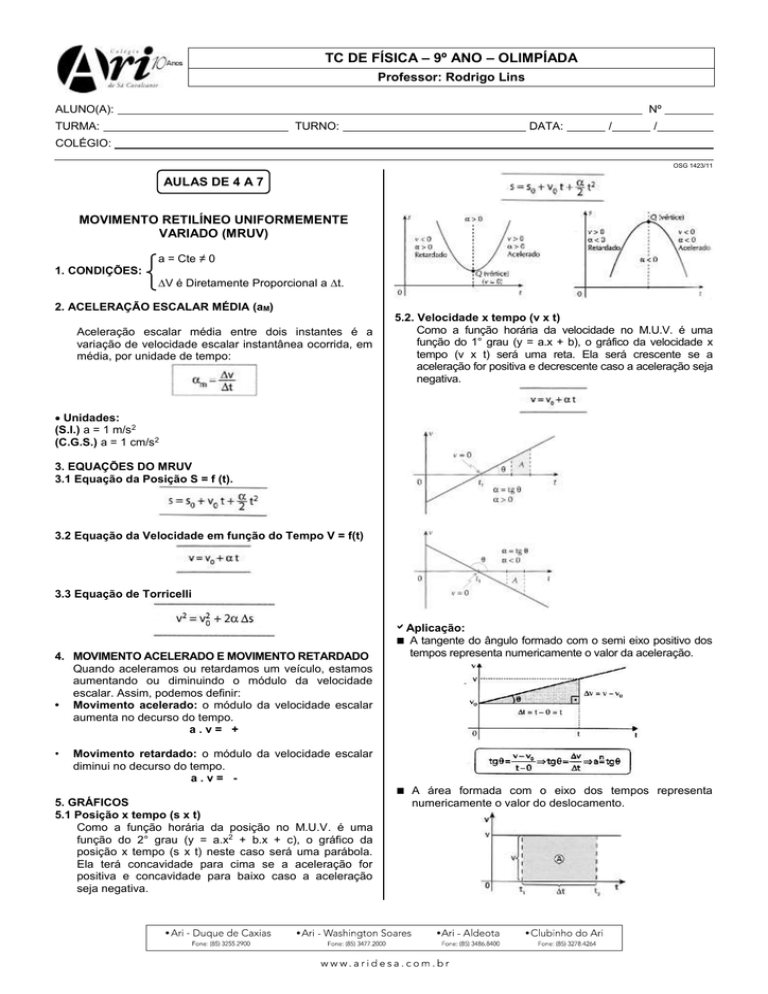
5.2. Velocidade x tempo (v x t)
Como a função horária da velocidade no M.U.V. é uma
função do 1° grau (y = a.x + b), o gráfico da velocidade x
tempo (v x t) será uma reta. Ela será crescente se a
aceleração for positiva e decrescente caso a aceleração seja
negativa.
 Unidades:
(S.I.) a = 1 m/s2
(C.G.S.) a = 1 cm/s2
3. EQUAÇÕES DO MRUV
3.1 Equação da Posição S = f (t).
3.2 Equação da Velocidade em função do Tempo V = f(t)
3.3 Equação de Torricelli
4. MOVIMENTO ACELERADO E MOVIMENTO RETARDADO
Quando aceleramos ou retardamos um veículo, estamos
aumentando ou diminuindo o módulo da velocidade
escalar. Assim, podemos definir:
• Movimento acelerado: o módulo da velocidade escalar
aumenta no decurso do tempo.
a.v= +
•
Aplicação:
 A tangente do ângulo formado com o semi eixo positivo dos
tempos representa numericamente o valor da aceleração.
Movimento retardado: o módulo da velocidade escalar
diminui no decurso do tempo.
a.v= -
5. GRÁFICOS
5.1 Posição x tempo (s x t)
Como a função horária da posição no M.U.V. é uma
função do 2° grau (y = a.x2 + b.x + c), o gráfico da
posição x tempo (s x t) neste caso será uma parábola.
Ela terá concavidade para cima se a aceleração for
positiva e concavidade para baixo caso a aceleração
seja negativa.
 A área formada com o eixo dos tempos representa
numericamente o valor do deslocamento.
TC DE FÍSICA – 9º ANO – OLIMPÍADA
orientação da trajetória e não depende do fato de o corpo
estar subindo ou descendo.
Portanto:
5.3. Aceleração x tempo (a x t)
Como no M.U.V. a aceleração escalar permanece
constante com o decorrer do tempo, o gráfico da
aceleração x tempo (a x t) será uma reta paralela ao eixo
dos tempos. A reta será acima do eixo dos tempos se a
aceleração for positiva e abaixo desse eixo se a
aceleração for negativa.
As funções do MUV descrevem o lançamento na vertical e a
queda livre:
 Propriedades do Movimento Vertical
1°) Corpos abandonados num mesmo local e na mesma altura
em relação ao solo demoram o mesmo intervalo de tempo
para chegar ao solo, não importando as suas massas.
2°) Quando um corpo é lançado verticalmente para cima, a
velocidade com que ele passa por um ponto qualquer da
trajetória, na subida, tem o mesmo módulo da velocidade
com que ele passa pelo mesmo ponto, na descida.
Aplicação:
 O gráfico a x t, a área formada com o eixo dos tempos
representa numericamente o valor da variação da
velocidade escalar.
3°) O intervalo de tempo decorrido entre as passagens por
dois pontos A e B da trajetória é o mesmo na subida e na
descida.
EXERCÍCIOS DE FIXAÇÃO
1.
Um objeto A encontra-se parado quando por ele passa
um objeto B com velocidade constante de módulo igual a
8,0 m/s. No instante da ultrapassagem, imprime-se ao
objeto A uma aceleração, de módulo igual a 0,2 m/s 2, na
mesma direção e sentido da velocidade de B. Qual a
velocidade de A quando ele alcançar o objeto B?
a) 4,0 m/s
b) 8,0 m/s
c) 16,0 m/s
d) 32,0 m/s
e) 64,0 m/s
2.
A função horária do movimento de uma partícula é
expressa por S = t2 – 10.t + 24 (s em metros e t em
segundos). O espaço do móvel ao mudar de sentido é:
a) 24 m
d) 1 m
b) – 25 m
e) – 1 m
c) 25 m
3.
Um carro viaja com velocidade de 90 km/h (ou seja, 25 m/s)
num trecho retilíneo de uma rodovia quando, subitamente, o
motorista vê um animal parado na sua pista. Entre o
instante em que o motorista avista o animal e aquele em
que começa a frear, o carro percorre 15 m. Se o motorista
frear o carro à taxa constante de 5,0 m/s2, mantendo-o em
sua trajetória retilínea, ele só evitará atingir o animal, que
permanece imóvel durante todo o tempo, se o tiver
percebido a uma distância de, no mínimo,
a) 15 m.
b) 31,25 m.
c) 52,5 m.
d) 77,5 m.
e) 125 m.
LANÇAMENTO VERTICAL NO VÁCUO
Em campo gravitacional uniforme, sua aceleração escalar é
constante e diferente de zero. O módulo dessa aceleração é
dado por:
Na queda, o módulo da velocidade escalar do corpo
aumenta: o movimento é acelerado. Lançado verticalmente
para cima, o módulo da velocidade escalar diminui na subida:
o movimento é retardado.
Assim, num lançamento vertical e numa queda livre, o sinal
da aceleração escalar é determinado somente pela
2
OSG 1423/11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
4.
Um projétil de massa m = 5,00 g atinge
perpendicularmente uma parede com velocidade V = 400
m/s e penetra 10,0 cm na direção do movimento.
(Considere constante a desaceleração do projétil na
parede).
a) Se V = 600 m/s, a penetração seria de 15,0 cm
b) Se V = 600 m/s, a penetração seria de 225 cm
c) Se V = 600 m/s, a penetração seria de 22,5 cm
d) Se V = 600 m/s, a penetração seria de 150 cm
e) A intensidade da força imposta pela parede à
penetração da bala é 2 N
Podemos afirmar corretamente que entre os instantes:
a) 0 e t1 o movimento é retrógrado acelerado.
b) t1 e t2 o movimento é progressivo acelerado.
c) t2 e t3 o movimento é retrógrado acelerado.
d) t3 e t4 o móvel está parado.
e) t4 e t5 o movimento é progressivo retardado.
9.
Instruções: Para responder às questões 05 e 06,
considere as informações que seguem.
O gráfico fornece a velocidade de um corpo, que se move em
linha reta, em função do tempo.
Um projétil é lançado verticalmente para cima, a partir do
nível do solo, com velocidade inicial de 30 m/s.
Admitindo g = 10 m/s2 e desprezando a resistência do ar,
analise as seguintes afirmações a respeito do movimento
desse projétil.
I. 1 s após o lançamento, o projétil se encontra na
posição de altura 25 m com relação ao solo.
II. 3 s após o lançamento, o projétil atinge a posição de
altura máxima.
III. 5 s após o lançamento, o projétil se encontra na
posição de altura 25 m com relação ao solo.
Quais estão corretas?
a) Apenas I.
b) Apenas II.
c) Apenas III.
d) Apenas II e III.
e) I, II e III.
Sabe-se que, no instante t = 0, o corpo se encontra na
posição 20 m.
5.
A aceleração escalar do corpo no sistema internacional
de unidades é de:
a) – 2,0
b) – 0,50
c) 0,0
d) 1,0
e) 2,0
10. Uma pedra é abandonada do alto de um edifício de 32
andares. Sabe-se que a altura de cada andar é de 2,5 m.
Desprezando-se a resistência do ar, com que velocidade
a pedra chegará ao solo?
a) 20 m/s
d) 80 m/s
b) 40 m/s
e) 100 m/s
c) 60 m/s
6.
No instante t = 8,0 s, o corpo estará na posição:
a) – 40 m
b) – 20 m
c) 20 m
d) 40 m
e) 60 m
7.
Um corpo está se movendo com velocidade de 5,0 m/s
no instante em que passa a ter aceleração, como mostra
o gráfico abaixo. Ao final de 5,0 segundos, sua
velocidade será:
a) 9,0 m/s
b) 7,0 m/s
c) 3,0 m/s
d) 5,0 m/s
e) 6,0 m/s
11. Um garoto lança uma pequena bola, verticalmente para
cima, do topo de um edifício. A bola parte com
velocidade inicial de módulo 10 m/s e atinge o solo 4,0 s
após o lançamento. Desprezando-se a resistência do ar,
a altura do edifício é: (Use g = 10 m/s2)
a) 40 m
d) 160 m
b) 80 m
e) 200 m
c) 120 m
8.
12. Uma bola é abandonada do topo de um edifício de 50 m de
altura. No mesmo instante, outra bola é lançada, a partir
do solo, verticalmente para cima com velocidade inicial
vo = 20 m/s. As duas estarão na mesma horizontal
depois de: (Considerar g = 10 m/s 2 e desprezar a
resistência do ar.)
a) 2,0 s
b) 2,5 s
c) 4,9 s
d) 9,8 s
e) 10 s
13. De um helicóptero que desce verticalmente, é
abandonada uma pedra quando o mesmo se encontra a
100 m do solo. Sabendo que a pedra leva 4 s para atingir
o solo e supondo g = 10 m/s2, a velocidade de descida do
helicóptero, no momento em que a pedra é abandonada,
tem valor:
a) 25 m/s
b) 20 m/s
c) 15 m/s
d) 10 m/s
e) 5 m/s
Um móvel em movimento retilíneo tem velocidade
escalar v variando com o tempo t, de acordo com o
gráfico.
OSG 1423/11
3
TC DE FÍSICA – 9º ANO – OLIMPÍADA
14. Uma pedra cai em um poço e o observador ouve o som
da pedra no fundo após 9 s. Admitindo uma aceleração
de gravidade igual a 10 m/s 2 e a velocidade do som de
320 m/s, qual a profundidade do poço? Despreze a
resistência do ar.
a) 120 m
b) 220 m
c) 320 m
d) 420 m
e) 520 m
a) 7
b) 8
c) 9
EXERCÍCIOS PROPOSTOS
1.
Um veículo parte de um ponto A para um ponto B e
gasta nesse percurso 40 s, com aceleração constante de
3 m/s2 e velocidade inicial de 4 m/s. Podemos afirmar
que a distância entre os dois pontos é de:
a) 960 m
b) 1.280 m
c) 1.840 m
d) 2.560 m
e) 3.880 m
d) 10
e) 11
7.
Um automóvel parte do repouso com M.R.U.V. e, após
percorrer a distância d, sua velocidade é v. A distância
que esse automóvel deverá ainda percorrer para que sua
velocidade seja 2v será:
a) d/2
d) 3d
b) d
e) 4d
c) 2d
8.
Uma motocicleta, com velocidade de 90 km/h, tem seus
freios acionados bruscamente e para após 25 s. Qual é a
distância percorrida pela motocicleta desde o instante em que
foram acionados os freios até a parada total da mesma?
a) 25 m
d) 360 m
b) 50 m
e) 312,5 m
c) 90 m
Nota do autor: admitir que a função horária é válida no
Sistema Internacional de Unidades.
2.
Um corpo, movendo-se ao longo do eixo dos x com uma
aceleração constante, passa na origem com uma
velocidade de 6 cm/s para a direita. Após 2 segundos,
sua abscissa é 8 cm à direita da origem. Pode-se então
concluir que sua aceleração é:
a) 2 cm/s2 para a direita
b) 2 cm/s2 para a esquerda
c) 1 cm/s2 para a direita
d) 1 cm/s2 para a esquerda
9.
Dois móveis A e B tem equações horárias,
respectivamente iguais a: SA = 80 - 5.t e SB = 10 + 2.t2,
onde SA e SB estão em metros e t em segundos. Pode-se
afirmar que:
a) os móveis A e B têm posições iniciais,
respectivamente iguais a 10 m e 80 m.
b) o movimento de A é progressivo e de B retrógrado.
c) os movimentos de A e B têm velocidades constantes.
d) ambos têm movimentos progressivos.
e) o móvel A tem velocidade constante e B aceleração
constante.
3.
Um
ponto
material
com
movimento
retilíneo
uniformemente variado passa pelo ponto A de uma reta
com velocidade de 15 m/s, dirigindo-se para o ponto B
dessa mesma reta. Se a distância AB é de 40 m e o
intervalo de tempo desse percurso é de 5,0 s, a
velocidade desse ponto material ao passar por B é de:
a) 30 m/s
d) 5,0 m/s
b) 15 m/s
e) 1,0 m/s
c) 10 m/s
10. Um trem de 120 m de comprimento se desloca com
velocidade escalar de 20 m/s. Esse trem, ao iniciar a
travessia de uma ponte, freia uniformemente, saindo
completamente da mesma 10 s após com velocidade
escalar de 10 m/s. O comprimento da ponte é:
a) 150 m
d) 60 m
b) 120 m
e) 30 m
c) 90 m
11. Um corpo se move em trajetória retilínea durante 2,0 s
conforme o gráfico abaixo.
Para responder às questões de 04 a 06, utilize as
informações abaixo.
Uma partícula tem velocidade escalar variável dada pela
equação v = 3 + 6.t. Sabemos que no instante t = 0 a
partícula estava num ponto situado a 6 m do ponto de
referência zero, por onde a partícula ainda vai passar.
Considere que as unidades representadas nas equações
são as do SI.
4.
A equação horária para a partícula deve ser:
a) s = 6 + 3.t + 6.t2
b) s = 6 – 3.t + 3.t2
c) s = – 6 – 3.t – 3.t2
d) s = – 6 + 3.t + 3.t2
e) s = – 6 + 3.t + 6.t2
5.
No instante em que a partícula tinha velocidade zero, a
posição era dada por s igual a:
a) zero
d) – 8,75
b) – 5
e) – 9,75
c) – 6,75
No instante em que a partícula passava pela posição
zero de referência, a velocidade tinha módulo:
6.
Analise as afirmativas a seguir:
I. Ao final do movimento, o corpo terá percorrido 25 m.
II. Sua velocidade final é de 40 m/s e a velocidade
média no percurso foi de 25 m/s.
III. A aceleração entre t = 1,0 s e t = 2,0 s foi de 10 m/s2.
Assinale:
a) se todas as afirmativas são corretas.
4
OSG 1423/11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
b)
c)
d)
e)
se todas asa afirmativas são falsas.
se apenas as afirmativas I e II são corretas.
se apenas as afirmativas II e III são corretas.
se apenas as afirmativas I e III são corretas.
maior velocidade que o trem atinge é de 20 m/s. O
tempo mínimo para o trem completar o percurso de A a
B é, em segundos, de:
a) 98
d) 196
b) 100
e) 204
c) 148
12. Um móvel está em movimento sobre um eixo orientado.
No instante t = 0, o móvel está na origem. A velocidade
escalar v do móvel está representada no gráfico a seguir
em função do tempo t.
16. Uma pedra, partindo do repouso, cai livremente no vácuo
durante 3 s. Se a aceleração da gravidade, suposta
uniforme, vale 10 m/s2, o corpo atingirá uma velocidade
de:
a) 3 m/s
c) 30 m/s
b) 10 m/s
d) 90 m/s
17. Uma pedra é atirada verticalmente para cima, com
velocidade inicial de módulo igual a 5,0 m/s. O módulo
da aceleração gravitacional local é 10,0 m/s 2.
Desprezando-se os atritos, o intervalo de tempo entre o
momento do lançamento e o instante em que a pedra
volta ao ponto de partida é igual, em segundos, a:
a) 0,50
d) 2,0
b) 1,0
e) 2,5
c) 1,5
No instante t = 5,0 s, o móvel estará num ponto cuja
distância até a origem, em metros, é igual a:
a) 30
d) 60
b) 45
e) 100
c) 50
13. O gráfico representa a variação da velocidade, com o
tempo, de um móvel em movimento retilíneo
uniformemente variado.
18. Um corpo é lançado do solo verticalmente para cima
com velocidade inicial tal que ele atinge uma altura
máxima de 2 km. Use g = 10 m/s2 e considere a
resistência do ar desprezível. Passados 15 s do seu
lançamento, o módulo da velocidade do projétil será de:
a) 30 m/s
d) 60 m/s
b) 45 m/s
e) 75 m/s
c) 50 m/s
19. Um chuveiro, situado a uma altura de 1,8 m do solo,
indevidamente fechado, deixa cair pingos de água a uma
razão constante de 4 pingos/segundo. No instante de
tempo em que um dado pingo toca o solo, o número de
pingos, atrás dele, que já estão a caminho é (use o valor
da aceleração da gravidade g = 10 m/s 2).
a) 0
d) 3
b) 1
e) 4
c) 2
A velocidade inicial do móvel e o seu deslocamento
escalar de 0 a 5,0 s valem, respectivamente:
a) - 4,0 m/s e - 5,0 m
b) - 6,0 m/s e - 5,0 m
c) 4,0 m/s e 25 m
d) - 4,0 m/s e 5,0 m
e) - 6,0 m/s e 25 m
20. Um objeto foi jogado verticalmente para cima e atingiu
uma altura de 125 m. Adotando g = 10 m/s2, o tempo de
permanência no ar foi de:
a) 2,0 s
d) 10,0 s
b) 7,5 s
e) 12,5 s
c) 8,0 s
14. Em uma experiência de decolagem de um avião a jato, a
força do motor é programada de modo que a aceleração
varia, como aparece no gráfico, durante os 12 segundos
necessários para a decolagem, partindo do repouso. A
velocidade v de decolagem é, em m/s:
21. De um ponto a 80m do solo um pequeno objeto P é
abandonado e cai em direção ao solo. Outro corpo Q,
um segundo antes, havia sido atirado para baixo, na
mesma vertical, de um ponto a 180 m do solo. Adote g
= 10 m/s2 e despreze a ação do ar sobre os corpos.
Sabendo-se que eles chegam juntos ao solo, a
velocidade com que o corpo Q foi atirado tem módulo,
em m/s, de:
a) 100
b) 95
c) 50
d) 20
e) 11
22. Uma bola é solta de uma altura de 45,0 m e cai
verticalmente. Um segundo depois, outra bola é
arremessada verticalmente para baixo. Sabendo que a
aceleração da gravidade no local é 10,0 m/s 2 e
a) 60
b) 45
c) 30
d) 15
e) 5
15. Um trem deve partir de uma estação A e parar na
estação B, distante 4.000 m de A. A aceleração e a
desaceleração podem ser, no máximo, de 5,0 m/s 2, e a
OSG 1423/11
5
TC DE FÍSICA – 9º ANO – OLIMPÍADA
desprezando a resistência do ar, a velocidade com que a
última bola deve ser arremessada, para que as duas
atinjam o solo no mesmo instante, é:
a) 12,5 m/s
d) 1,25 m/s
b) 7,50 m/s
e) 0,75 m/s
c) 75,0 m/s
altura h, alcançada por ele quando sua velocidade se
reduz à metade da inicial, equivale a:
a) H/2.
d) 4H/5.
b) H/4.
e) 3H/4.
c) 4H/3.
29. Uma pedra é abandonada de uma ponte, a 80 m acima
da água. Uma outra pedra é atirada verticalmente para
baixo, do mesmo local, dois segundos após o abandono
da primeira. Se as duas pedras atingem a água no
mesmo instante, e desprezando-se a resistência do ar,
calcule o módulo da velocidade inicial da segunda pedra,
considerando g = 10 m/s2.
a) 10 m/s
d) 40 m/s
b) 20 m/s
e) 50 m/s
c) 30 m/s
23. Um corpo é abandonado a uma certa altura e leva 4,0 s
para tocar o solo. Desprezando a resistência do ar e
sendo g = 10 m/s2, a velocidade média desse corpo nos
4,0 s é:
a) 10 m/s
d) 60 m/s
b) 20 m/s
e) 80 m/s
c) 40 m/s
24. O gráfico a seguir representa a velocidade de um objeto
lançado verticalmente para cima, desprezando-se a ação
da atmosfera.
30. Um móvel é abandonado em queda livre percorrendo, a
partir do repouso, uma distância d durante o primeiro
segundo de movimento. Durante o terceiro segundo de
movimento, esse móvel percorre uma distância:
a) 2.d
d) 7.d
b) 3.d
e) 9.d
c) 5.d
GABARITO DOS EXERCÍCIOS DE FIXAÇÃO
AULAS DE 4 A 7
01.
02.
03.
04.
05.
06.
07.
C
E
D
C
B
E
B
08.
09.
10.
11.
12.
13.
14.
C
E
B
A
B
E
C
Assinale a afirmativa INCORRETA.
a) O objeto atinge, 2 segundos após o lançamento, o
ponto mais alto da trajetória.
b) A altura máxima atingida pelo objeto é 20 metros.
c) O deslocamento do objeto, 4 segundos após o
lançamento, é zero.
d) A aceleração do objeto permanece constante
durante o tempo observado e é igual a 10 m/s2.
e) A velocidade inicial do objeto é igual a 20 m/s.
GABARITO DOS EXERCÍCIOS PROPOSTOS
AULAS DE 4 A 7
01.
02.
03.
04.
05.
D
B
E
D
C
06.
07.
08.
09.
10.
C
D
E
E
E
11.
12.
13.
14.
15.
E
A
B
B
E
16.
17.
18.
19.
20.
C
B
C
C
D
21.
22.
23.
24.
25.
E
A
B
D
B
26.
27.
28.
29.
30.
D
A
E
C
C
25. Em um circo, um malabarista lança bolas, verticalmente
para cima, que atingem uma altura máxima h. No caso
de jogá-las para que elas fiquem o dobro do tempo no ar,
a nova altura máxima será:
a) 2.h
c) 6.h
b) 4.h
d) 8.h
26. Um foguete sobe verticalmente. No instante t = 0 em que
ele passa pela altura de 100 m, em relação ao solo,
subindo com velocidade constante de módulo 5,0 m/s,
escapa dele um pequeno parafuso. Considere g = 10 m/s2 e
despreze o efeito do ar. O parafuso chegará ao solo no
instante t, em segundos, igual a:
a) 20
d) 5,0
b) 15
e) 3,0
c) 10
27. Um garoto que se encontra em uma ponte está 20 m
acima da superfície de um rio. No instante em que a proa
(frente) de um barco, com movimento retilíneo uniforme,
atinge a vertical que passa pelo garoto, ele abandona
uma pedra que atinge o barco em um ponto localizado a
180 cm do ponto visado. A velocidade do barco é:
a) 0,90 m/s
d) 10 m/s
b) 1,20 m/s
e) 20 m/s
c) 1,60 m/s
AULAS DE 8 A 10
VETORES
1.
28. Um corpo lançado verticalmente para cima, no vácuo,
com velocidade inicial v0, atinge a altura máxima H. A
6
Introdução
Vetor é o símbolo matemático utilizado para representar
o módulo, a direção e o sentido de uma grandeza física
OSG 1423/11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
vetorial. O vetor é representado por meio de uma seta
com origem O e extremidade P.
3ª) Se os dois vetores tiverem a mesma direção e sentidos
opostos (θ = 180°), o vetor resultante será:
A indicação algébrica de um vetor é feita da seguinte
forma: v = OP = P – O. Para que um vetor fique
caracterizado, é preciso conhecer seu módulo ou
intensidade, direção e seu sentido.
2.
Vetores Iguais
Dois vetores a e b são iguais quando têm a mesma
direção, o mesmo sentido e o mesmo módulo. Se pelo
menos uma dessas características difere, eles são
chamados vetores diferentes.
5.
Colocando esses dois vetores a partir de uma origem
comum: podemos achar o vetor diferença entre eles da
seguinte forma:
3. Vetores Opostos
Dois vetores são opostos quando têm a mesma direção,
o mesmo módulo e sentidos contrários.
4.
Operações com Vetores
Consideremos os vetores a e b indicados na figura.
Operações com Vetores
Dados os vetores a = A  O e b = B  O, o vetor soma =
resultante R é obtido graficamente traçando-se pelas
extremidades de cada um deles uma paralela ao outro.
6.
Decomposição Vetorial
Consideremos o vetor a e os eixos x e y.
Na figura, R é o vetor soma. Como a figura formada é
paralelogramo, esse método é denominado método do
paralelogramo. A intensidade do vetar soma é dada por:
OBS:
1ª) Se os dois vetores forem perpendiculares entre si, para obter
o vetor resultante basta aplicar o teorema de Pitágoras.
Projetando, perpendicularmente, o vetor a nos eixos x e
y, obtemos suas componentes retangulares ax e ay. Da
figura temos:
7.
2ª) Se os dois vetores tiverem a mesma direção e o mesmo
sentido (θ = 0°), o vetor resultante será:
e
Composição de movimentos
O movimento resultante de um corpo, ao descrever uma
trajetória qualquer, é, muitas vezes, composto por mais
de um movimento.
Exemplos:
a) a velocidade de um barco ao atravessar um rio;
OSG 1423/11
7
TC DE FÍSICA – 9º ANO – OLIMPÍADA
3.
Num plano , temos dois vetores a e b de mesma
origem formando um ângulo . Se os módulos de a e de
b são, respectivamente, iguais a 3 u e 4 u, determine o
módulo do vetor soma em cada um dos casos seguintes:
a)  = 0°
c)  = 180°
b)  = 90°
d)  = 60°
b)
a velocidade de um avião.
4.
u e v,
Considere
dois
vetores,
de
módulos
respectivamente iguais a 10 unidades e 15 unidades.
Qual o intervalo de valores admissíveis para o módulo do
vetor S, soma de u com v ?
5.
Dois vetores a e b , de mesma origem, formam entre si
um ângulo  = 60°. Se os módulos desses vetores são
a = 7 u e b = 8 u, qual o módulo do vetor soma?
OBS: Galileu Galilei, observando a composição dos movimentos, concluiu que podia estudar o movimento resultante
de um corpo analisando separadamente os movimentos que
o compõem e enunciou o princípio da independência dos
movimentos, que diz:
“Se um corpo se encontra sob a ação simultânea de vários
movimentos, cada um deles se processa como se os demais
não existissem.”
6.
Qual é o módulo da resultante das forças coplanares
M , N , P e Q e aplicadas ao ponto O, como se mostra
na figura abaixo?
EXERCÍCIOS DE FIXAÇÃO
1.
A respeito das grandezas físicas escalares e vetoriais,
analise as proposições a seguir:
(01) As escalares ficam perfeitamente definidas,
mediante um valor numérico acompanhado da
respectiva unidade de medida.
(02) As vetoriais, além de exigirem na sua definição um
valor numérico, denominado módulo ou intensidade,
acompanhado da respectiva unidade de medida,
requerem, ainda, uma direção e um sentido.
(04) Comprimento, área, volume, tempo e massa são
grandezas escalares.
(08) Deslocamento, velocidade, aceleração e força são
grandezas vetoriais.
Dê como resposta a soma dos números associados às
proposições corretas.
2.
7.
Considere as seguintes grandezas físicas mecânicas:
TEMPO, MASSA, FORÇA, VELOCIDADE e TRABALHO.
Dentre elas, têm caráter vetorial apenas
a) força e velocidade.
b) massa e força.
c) tempo e massa.
d) velocidade e trabalho.
e) tempo e trabalho.
8.
Sabe-se que a distância entre as margens paralelas de
um rio é de 100 m e que a velocidade da correnteza, de
6 m/s, é constante, com direção paralela às margens.
Um barco parte de um ponto x da margem A com
velocidade constante de 8 m/s, com direção
perpendicular às margens do rio. A que distância do
ponto x o barco atinge a margem B?
a) 100 m
b) 125 m
c) 600 m
d) 750 m
e) 800 m
No lançamento de um bumerangue, este afasta-se até a
distância de 32 m e, após 8,0 s, volta onde está o dono
que o atira. A velocidade vetorial média nesse intervalo
de tempo tem módulo:
a) 16 m/s
b) 8,0 m/s
c) 4,0 m/s
d) 2,0 m/s
e) zero
Na figura, temos três vetores coplanares formando uma
linha poligonal fechada. A respeito da figura, vale a relação:
9.
8
OSG 1423/11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
10. Quatro bolas de futebol, com raios e massas iguais,
foram lançadas verticalmente para cima, a partir do piso
de um ginásio, em instantes diferentes. Após um
intervalo de tempo, quando as bolas ocupavam a mesma
altura, elas foram fotografadas e tiveram seus vetores
velocidade identificados conforme a figura a seguir:
b) a velocidade de todos os estudantes que eu consigo
enxergar agora assentados em seus lugares é nula
para qualquer observador.
c) mesmo para o professor, que não para de andar,
seria possível achar um referencial em que ele
estivesse em repouso.
d) eu estou em repouso em relação aos meus colegas,
mas todos nós estamos em movimento em relação à
Terra.
13. Um avião, voando a 240 m/s em relação ao ar, numa
altitude onde a velocidade do som é de 300 m/s, dispara
um míssil que parte a 260 m/s em relação ao avião.
Assim, as velocidades do míssil em relação ao ar e da
onda sonora originada no disparo serão, respectivamente,
a) 260 m/s e 40 m/s.
b) 260 m/s e 60 m/s.
c) 260 m/s e 300 m/s.
d) 500 m/s e 300 m/s.
e) 500 m/s e 540 m/s.
Desprezando a resistência do ar, considere as seguintes
afirmativas:
I. No instante indicado na figura, a força sobre a bola
b4 é maior que a força sobre a bola b3.
II. É possível afirmar que b4 é a bola que atingirá a
maior altura a partir do solo.
III. Todas as bolas estão igualmente aceleradas para
baixo.
14. Num estacionamento, um coelho se desloca, em
sequência, 12 m para o Oeste, 8 m para o Norte e 6 m
para o Leste. O deslocamento resultante tem módulo
a) 26 m
d) 10 m
b) 14 m
e) 2 m
c) 12 m
Assinale a alternativa correta.
a) Somente a afirmativa I é verdadeira.
b) Somente a afirmativa II é verdadeira.
c) Somente a afirmativa III é verdadeira.
d) Somente as afirmativas II e III são verdadeiras.
e) Somente as afirmativas I e III são verdadeiras.
15. Na figura a seguir, onde o reticulado forma quadrados de
lados ℓ = 0,5cm, estão desenhados 10 vetores contidos
no plano xy. O módulo da soma de todos esses vetores
é, em centímetros:
a) 0,0.
b) 0,5.
c) 1,0.
d) 1,5.
e) 2,0.
11. Um ônibus percorre em 30 minutos as ruas de um bairro,
de A até B, como mostra a figura:
16. Uma lancha, subindo um rio, percorre, em relação às
margens, 2,34 km em 1 hora e 18 minutos. Ao descer o
rio, percorre a mesma distância em 26 minutos. Observase que, tanto na subida como na descida, o módulo da
velocidade da lancha em relação à água é o mesmo. O
módulo da velocidade da correnteza, em relação às
margens, é:
a) 5,4 km/h
b) 4,5 km/h
c) 3,6 km/h
d) 2,7 km/h
e) 1,8 km/h
17. A figura representa um avião, que mergulha fazendo um
ângulo de 30° com a horizontal, seguindo uma trajetória
retilínea entre os pontos A e B. No solo, considerado
como plano horizontal, está representada a sombra da
aeronave, projetada verticalmente, e um ponto de
referência C.
Considerando a distância entre duas ruas paralelas
consecutivas igual a 100 m, analise as afirmações:
I. A velocidade vetorial média nesse percurso tem
módulo 1 km/h.
II. O ônibus percorre 1500 m entre os pontos A e B.
III. O módulo do vetor deslocamento é 500 m.
IV. A velocidade vetorial média do ônibus entre A e B
tem módulo 3 km/h.
Estão corretas:
a) I e III.
d) I e II.
b) I e IV.
e) II e III.
c) III e IV.
12. Um estudante, observando seus colegas assentados em
seus lugares e recordando seus conceitos de
movimento, julga CORRETAMENTE que:
a) como não há repouso absoluto, nenhum de nós está
em repouso em relação a nenhum referencial.
OSG 1423/11
9
TC DE FÍSICA – 9º ANO – OLIMPÍADA
e) espaço percorrido, o deslocamento e a velocidade
vetorial média são iguais.
20. Um veículo de massa 500 kg, percorrendo uma estrada
horizontal, entra numa curva com velocidade de 50 km/h e
sai numa direção que forma ângulo de 60° com a direção
inicial e com a mesma velocidade de 50 km/h. Em
unidades do Sistema Internacional, a variação da
quantidade de movimento do veículo ao fazer a curva,
em módulo, foi de:
a) 7,0 . 104
b) 5,0 . 104
c) 3,0 . 104
d) 7,0 . 103
e) 3,0 . 103
Considere as afirmativas que se referem ao movimento da
aeronave no trecho AB, e assinale a alternativa correta:
a) A velocidade do avião em relação ao ponto C é
maior que a velocidade de sua sombra, projetada no
solo, em relação ao mesmo ponto.
b) A velocidade do avião é nula em relação à sua
sombra projetada no solo.
c) A velocidade do avião em relação ao ponto C é igual
à velocidade de sua sombra, projetada no solo em
relação ao mesmo ponto.
d) A velocidade do avião em relação à sua sombra
projetada no solo é maior que a velocidade de sua
sombra em relação ao ponto C.
e) A velocidade da sombra em relação ao ponto C
independe da velocidade do avião.
21. Com seis vetores de módulo igual a 8u, construiu-se o
hexágono regular a seguir. O módulo do vetor resultante
desses 6 vetores é:
a) 40 u
b) 32 u
c) 24 u
d) 16 u
e) zero
EXERCÍCIOS PROPOSTOS
18. Um menino flutua em uma boia que está se
movimentando, levada pela correnteza de um rio. Uma
outra bóia, que flutua no mesmo rio a uma certa
distância do menino, também está descendo com a
correnteza. A posição das duas boias e o sentido da
correnteza estão indicados nesta figura:
1.
Num bairro, onde todos os quarteirões são quadrados e
as ruas paralelas distam 100 m uma da outra, um
transeunte faz o percurso de P a Q pela trajetória
representada no esquema a seguir.
O deslocamento vetorial desse transeunte tem módulo,
em metros, igual a
a) 300
b) 350
c) 400
d) 500
e) 700
Considere que a velocidade da correnteza é a mesma
em todos os pontos do rio. Nesse caso, para alcançar a
segunda boia, o menino deve nadar na direção indicada
pela linha
a) K.
b) L.
c) M.
d) N.
19. Nas provas dos 200 m rasos, no atletismo, os atletas
partem de marcas localizadas em posições diferentes na
parte curva da pista e não podem sair de suas raias até
a linha de chegada. Dessa forma, podemos afirmar que,
durante a prova, para todos os atletas, o
a) espaço percorrido é o mesmo, mas o deslocamento
e a velocidade vetorial média são diferentes.
b) espaço percorrido e o deslocamento são os mesmos,
mas a velocidade vetorial média é diferente.
c) deslocamento é o mesmo, mas o espaço percorrido
e a velocidade vetorial média são diferentes.
d) deslocamento e a velocidade vetorial média são
iguais, mas o espaço percorrido é diferente.
2.
10
Uma partícula move-se no plano segundo a trajetória da
linha sólida mostrada na figura ao lado. O módulo da
velocidade da partícula é de 40 m/s e constante durante
seu movimento. Determine o módulo da velocidade
vetorial média da partícula no intervalo de tempo
compreendido entre os pontos P e Q de sua trajetória.
OSG 1423/11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
a) 20 m/s
b) 40 m/s
c) 80 m/s
3.
4.
perpendicular às margens do rio. A que distância do
ponto x o barco atinge a margem B?
a) 100 m
d) 750 m
b) 125 m
e) 800 m
c) 600 m
d) 120 m/s
e) 160 m/s
Um rio de margens retilíneas e largura constante igual a
5,0 km tem águas que correm paralelamente às
margens, com velocidade de intensidade 30 km/h. Um
barco, cujo motor lhe imprime velocidade de intensidade
sempre igual a 50 km/h em relação às águas, faz a
travessia do rio.
a) Qual o mínimo intervalo de tempo possível para que
o barco atravesse o rio?
b) Na condição de atravessar o rio no intervalo de
tempo mínimo, que distância o barco percorre
paralelamente às margens?
c) Qual o intervalo de tempo necessário para que o
barco atravesse o rio percorrendo a menor distância
possível?
GABARITO DOS EXERCÍCIOS DE FIXAÇÃO
AULAS DE 8 A 10
01.
02.
03.
04.
05.
06.
07.
*
C
**
***
13 u
5N
A
08.
09.
10.
11.
12.
13.
14.
B
E
D
A
C
D
D
15.
16.
17.
18.
19.
20.
21.
E
E
A
A
A
D
B
01. * Soma 15
03. ** a) 7u b) 5u c) 1u d)  6u
04. *** 5 unidades  s  25 unidades
GABARITO DOS EXERCÍCIOS PROPOSTOS
AULAS DE 8 A 10
01.
02.
03.
04.
05.
06.
07.
D
C
*
C
D
A
B
03. * a) 6 min b) 3 km c) 7,5 min
Um caminhoneiro efetuou duas entregas de mercadorias
e, para isso, seguiu o itinerário indicado pelos vetores
deslocamentos d1 e d2‚ ilustrados na figura. Para a
primeira entrega, ele deslocou-se 10 km e para a
segunda entrega, percorreu uma distância de 6 km. Ao
final da segunda entrega, a distância a que o
caminhoneiro se encontra do ponto de partida é
a) 4 km.
b) 8 km.
c) 2 19 km.
d) 8 3 km.
e) 16 km.
5.
Um barco movido por motor desce 120 km de rio em 2 h.
No sentido contrário, demora 3 h para chegar ao ponto
de partida. Qual é a velocidade da água do rio? Sabe-se
que, na ida e na volta, a potência desenvolvida pelo
motor é a mesma.
a) 15 km/h
d) 10 km/h
b) 20 km/h
e) 48 km/h
c) 30 km/h
6.
AULAS DE 11 A 13
A velocidade vetorial média de um carro de Fórmula 1
em uma volta completa do circuito corresponde a:
a) 0
c) 191
b) 24
d) 240
7.
Lançamentos não verticais (Lançamento oblíquo e
Lançamento horizontal)
A maioria dos movimentos que observamos no dia-a-dia não
são movimentos simples de serem descritos matematicamente;
na verdade, são movimentos complexos, dois ou mais
movimentos diferentes que se realizam simultaneamente. Se a
partícula estiver no vácuo, sujeita somente à aceleração da
gravidade, o movimento horizontal será uniforme (M.U.) Se o
movimento vertical será uniformemente variado (M.U.V.).
Sabe-se que a distância entre as margens paralelas de
um rio é de 100 m e que a velocidade da correnteza, de
6 m/s, é constante, com direção paralela às margens.
Um barco parte de um ponto x da margem A com
velocidade constante de 8 m/s, com direção
OSG 1423/11
11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
1.
Decomposição do Movimento Parabólico Horizontal
e Vertical
Eixo X (Horizontal)
M.R.U.
ax = 0
Eixo Y(Vertical)
a = + g (Descida)
a =  g (Subida)
2.
3.
M.R.U.V.
Lançamento Horizontal
Considere o lançamento de um corpo com velocidade
inicial Vo estritamente horizontal, a partir de uma altura h.
De acordo com o princípio da independência dos
movimentos simultâneos de Galileu, podemos considerar
o movimento descrito pela bola como resultante da
composição de dois movimentos mais simples e que
ocorrem simultaneamente: uma queda livre na vertical e
um movimento uniforme horizontal.
Lançamento oblíquo – Descrição Matemática
Analisaremos cada projeção do movimento separadamente.
3.1 (Eixo – X) Movimento Horizontal (M.U.)
vx = vo = cte ≠ 0
Condições:
ax = 0 (Nula)
onde:
eixo x
eixo y
(Função de s x t no eixo X)
vox = vo . cos
voy = vo . cos
S = S0 + V . t
2.1) (Eixo – X) Movimento Horizontal (M.U.)
3.2 (Eixo–Y) Movimento Vertical (M.U.V)
Vx = Vox = cte ≠ 0
Condições:
V0y = 0
Condições:
ax = 0 (Nula)
Na Descida
α=+g
(Função de s x t no eixo X)
(Função de s x t no eixo Y)
S = S0 + V . t
2.2) (Eixo–Y) Movimento Vertical (M.U.V)
 Na Subida
 Na Descida
α = - g.
α = + g.
(Função de v x t no eixo Y)
(Função de s x t no eixo Y)
(Equação de Torricelli no Eixo Y)
(Função de v x t no eixo Y)
EXERCÍCIOS
(Equação de Torricelli no Eixo Y)
1.
Observações:
•
O alcance horizontal de um projétil será máximo quando
o ângulo de lançamento for igual a 45º.
•
Para valores fixados de Vo e de g, objetos lançados com
ângulos de lançamento complementares têm alcances
horizontais iguais.
•
O tempo de subida é igual ao tempo de descida.
12
O "tira teima" da Rede Globo de televisão calculou a
velocidade da bola que bateu na trave do gol como
sendo de 1,1 × 102km/h. Se o tempo necessário para a bola
atingir a trave, desde quando foi chutada, é de 0,5 s, e
sendo a velocidade constante nesse tempo, pode-se
afirmar que a distância que a bola estava do gol,
imediatamente antes do chute, era da ordem de:
a) 25 m.
b) 15 m.
c) 55 m.
d) 40 m.
e) 30 m.
OSG 1423/11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
2.
3.
4.
Uma esfera de aço de massa 200 g desliza sobre uma
mesa plana com velocidade igual a 2 m/s. A mesa está a
1,8 m do solo. A que distância da mesa a esfera irá tocar
o solo? Obs.: despreze o atrito. Considere g = 10 m/s2.
a) 1,25 m
b) 0,5 m
c) 0,75 m
d) 1,0 m
e) 1,2 m
A altura máxima h alcançada pela bola e o deslocamento
horizontal x do carrinho, valem, respectivamente:
a) h = 16,2 m; x = 18,0 m
b) h = 16,2 m; x = 9,0 m
c) h = 8,1 m; x = 9,0 m
d) h = 10,0 m; x = 18,0 m
Um projétil é atirado com velocidade de 40m/s, fazendo
ângulo de 37° com a horizontal. A 64 m do ponto de
disparo, há um obstáculo de altura 20 m. Adotando g=10
m/s2, cos37°=0,80 e sen37°=0,60, pode-se concluir que
o projétil:
a) passa à distância de 2,0 m acima do obstáculo.
b) passa à distância de 8,0 m acima do obstáculo.
c) choca-se com o obstáculo a 12 m de altura.
d) choca-se com o obstáculo a 18 m de altura.
e) cai no solo antes de chegar até o obstáculo.
7.
Um corpo é lançado obliquamente com velocidade V0
de módulo 50 m/s, sob um ângulo de lançamento sen 
= 0,6; cos  = 0,8, conforme indica a figura:
Calcule, considerando g = 10 m/s 2 e desprezando a
influência do ar:
Um projétil de massa 100 g é lançado obliquamente a
partir do solo, para o alto, numa direção que forma 60°
com a horizontal com velocidade de 120 m/s, primeiro na
Terra e posteriormente na Lua. Considerando a
aceleração da gravidade da Terra o sêxtuplo da
gravidade lunar, e desprezíveis todos os atritos nos dois
experimentos, analise as proposições a seguir:
I. A altura máxima atingida pelo projétil é maior na Lua
que na Terra.
II. A velocidade do projétil, no ponto mais alto da
trajetória, será a mesma na Lua e na Terra.
III. O alcance horizontal máximo será maior na Lua.
IV. A velocidade com que o projétil toca o solo é a
mesma na Lua e na Terra.
Está correta ou estão corretas:
a) apenas III e IV.
b) apenas II.
c) apenas III.
d) todas.
e) nenhuma delas.
8.
a) a intensidade da velocidade v do corpo ao passar
pelo vértice do arco de parábola.
b) o tempo de subida.
c) a altura máxima (hmáx).
d) o alcance horizontal (A).
5.
6.
Uma menina chamada Clara de Assis, especialista em
salto à distância, consegue, na Terra, uma marca de 8,0 m.
Na Lua, onde a aceleração da gravidade é 1/6 de seu
valor na Terra, a atleta conseguiria saltar, mantidas
idênticas condições de salto:
a) 8 m
c) 48 m
b) 16 m
d) 96 m
Uma bola é lançada verticalmente para cima, com
velocidade de 18 m/s, por um rapaz situado em carrinho
que avança segundo uma reta horizontal, a 5,0 m/s.
Depois de atravessar um pequeno túnel, o rapaz volta a
recolher a bola, a qual acaba de descrever uma parábola,
conforme a figura. Despreza-se a resistência do ar e g =
10m/s2.
Um projétil é lançado segundo um ângulo de 30° com a
horizontal, com uma velocidade de 200 m/s. Supondo a
aceleração da gravidade igual e 10 m/s2 e desprezando
a resistência do ar, o intervalo de tempo entre as
passagens do projétil pelos pontos de altura 480 m
acima do ponto de lançamento, em segundos, é:
DADOS:
sen 30° = 0,50
cos 30° = 0,87
a) 2,0
b) 4,0
9.
c) 6,0
d) 8.0
e) 12
Um projétil é lançado numa direção que forma um ângulo
de 45° com a horizontal. No ponto de altura máxima, o
módulo da velocidade desse projétil é 10 m/s.
Considerando-se que a resistência do ar é desprezível,
pode-se concluir que o módulo da velocidade de
lançamento é, em m/s, igual a
a) 2,5 2
c) 10
e) 20
b) 5 2
d) 10 2
10. Dois rifles são disparados com os canos na horizontal,
paralelos ao plano do solo e ambos à mesma altura
acima do solo. À saída dos canos, a velocidade da bala
do rifle A é três vezes maior que a velocidade da bala do
rifle B. Após intervalos de tempo tA e tB, as balas atingem
o solo a, respectivamente, distâncias d A e dB das saídas
OSG 1423/11
13
TC DE FÍSICA – 9º ANO – OLIMPÍADA
dos respectivos canos. Desprezando-se a resistência do
ar, pode-se afirmar que:
a) tA = tB, dA = dB
b) tA = tB/3, dA = dB
c) tA = tB/3, dA = 3dB
d) tA = tB, dA = 3dB
e) tA = 3tB, dA = 3dB
lançamento. Desprezando a resistência do ar e a altura
do atleta, o intervalo de tempo t, em segundos, é um
valor mais próximo de:
Dados: g = 10 m/s2 e sen 45° = cos 45° = 0,7
11. Um sapo, colocado em cima de um muro, salta no
instante t0 = 0 e chega ao ponto P do solo, como
representa a figura.
15. A figura abaixo mostra três trajetórias de uma bola de
futebol que é chutada de um mesmo ponto.
a) 3,2
b) 1,8
c) 1,2
d) 0,8
e) 0,4
Sejam “t” o tempo de permanência da bola no ar, “Vv” a
componente vertical da velocidade inicial da bola e “Vh”
a componente horizontal da velocidade inicial. Em
relação a essas três grandezas físicas e considerando as
três trajetórias a, b e c anteriores, livres da resistência do
ar, pode-se concluir que:
Desprezando a influência do ar e considerando g igual a
10 m/s2, calcule:
a) o módulo da componente vertical da velocidade
inicial do sapo;
b) o instante t em que ele atinge o solo;
c) o módulo da componente horizontal da velocidade do
sapo.
16. No instante t0 = 0, um projétil é atirado para cima com
ângulo de 45° em relação à horizontal, com velocidade
de módulo 80 2 m/s. Desprezando a influência do ar e
considerando g = 10 m/s2, determine:
a) o(s) instante(s) em que o projétil encontra-se a 140
metros acima do plano horizontal de lançamento;
b) o módulo da velocidade do projétil no instante t = 2 s.
12. Observando a parábola do dardo arremessado por um
atleta, um matemático resolveu obter uma expressão
que lhe permitisse calcular a altura y, em metros, do
dardo em relação ao solo, decorridos t segundos do
instante de seu lançamento (t = 0). Se o dardo chegou à
altura máxima de 20 m e atingiu o solo 4 segundos após
o seu lançamento, então, desprezada a altura do atleta,
a expressão que o matemático encontrou foi
a) y =  5t2 + 20t
b) y =  5t2 + 10t
c) y =  5t2 + t
d) y = 10t2 + 50
e) y = 10t2 + 10
17. Uma esteira transportadora lança minério horizontalmente
com velocidade v0. Considere desprezível a influência do ar
e adote g = 10 m/s2.
13. De uma mesma altura h e no mesmo instante t0 = 0, uma
bola A é abandonada a partir do repouso e outra bola, B,
é lançada horizontalmente.
Determine o intervalo das intensidades de v0 para que o
minério caia dentro da carroceria do caminhão.
18. Um projétil é lançado com velocidade inicial v0, fazendo
um ângulo de 60° com a superfície horizontal. No
instante em que sua velocidade atinge v0/2, o ângulo
entre o vetor velocidade e a superfície horizontal é:
a) 60°
c) 30°
e) 3
b) 45°
d) 0,0°
19. Um cano de irrigação, enterrado no solo, ejeta água a uma
taxa de 15 litros por minuto com uma velocidade de 10
m/s. A saída do cano é apontada para cima fazendo um
ângulo de 30° com o solo, como mostra a figura.
Despreze a resistência do ar e considere g = 10 m/s 2,
sen 30° = 0,50 e cos 30° = 0,87.
As bolas A e B atingem o solo nos instantes tA e tB, com
velocidades de módulos vA e vB respectivamente.
Desprezando influências do ar, é correto afirmar que:
14. Um atleta arremessa um dardo sob um ângulo de 45°
com a horizontal e, após um intervalo de tempo t, o
dardo bate no solo 16 m à frente do ponto de
14
OSG 1423/11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
a)
b)
c)
d)
e)
apenas III e IV.
apenas II.
apenas III.
todas.
nenhuma delas.
GABARITO DOS EXERCÍCIOS
AULAS DE 11 A 13
01.
02.
03.
04.
05.
06.
07.
08.
B
E
B
*
C
A
D
B
09.
10.
11.
12.
13.
14.
15.
16.
D
D
**
A
D
B
C
***
17.
18.
19.
20.
21.
22.
****
D
*****
C
D
D
04. *
a) 40 m/s
b) 3 s
c) 45 m
d) 240 m
11. **
a) 4,0 m/s
b) 1,2 s c) 3,0 m/s
16. ***
a) 2 s e 14 s b) 100 m/s
17. ****
2,5 m/s < v0 < 25 m/s
19. ***** 0,25 litro
Calcule quantos litros de água estarão no ar na situação
em que o jato d’água é contínuo do cano ao solo.
20. Um balão (aeróstato) sobe verticalmente com velocidade
constante de 10 m/s. Ao atingir a altura de 40 m, seu
piloto lança, horizontalmente, uma pedra com velocidade
de 30 m/s. Adote g = 10 m/s2. A distância da vertical que
passa pelo ponto de lançamento ao ponto em que a
pedra atinge o solo é:
a) 40 m
b) 80 m
c) 120 m
d) 240 m
e) 360 m
AULAS DE 14 A 16
MOVIMENTO CIRCULAR UNIFORME (M.C.U.)
21. Suponha que Cebolinha, para vencer a distância que o
separa da outra margem e livrar-se da ira da Mônica,
tenha conseguido que sua velocidade de lançamento, de
valor 10 m/s, fizesse com a horizontal um ângulo , cujo
sen  = 0,6 e cos  = 0,8. Desprezando-se a resistência
do ar, o intervalo de tempo decorrido entre o instante em
que Cebolinha salta e o instante em que atinge o alcance
máximo do outro lado é
Movimento circular uniforme é aquele cuja trajetória é uma
circunferência e cuja velocidade vetorial tem módulo constante.
1.
Velocidade escalar média angular (ω)
Considere agora as posições que uma partícula móvel
ocupa numa circunferência nos instantes t1 e t2.
Onde:
Deslocamento Angular (∆φ)
a)
b)
c)
d)
e)
Unidades:
ω = 1 rad / s. (radianos por segundo)
2,0 s
1,8 s
1,6 s
1,2 s
0,8 s
22. Um projétil de massa 100 g é lançado obliquamente a
partir do solo, para o alto, numa direção que forma 60°
com a horizontal com velocidade de 120 m/s, primeiro na
Terra e posteriormente na Lua. Considerando a
aceleração da gravidade da Terra o sêxtuplo da
gravidade lunar, e desprezíveis todos os atritos nos dois
experimentos, analise as proposições a seguir:
A altura máxima atingida pelo projétil é maior na Lua
que na Terra.
II. A velocidade do projétil, no ponto mais alto da
trajetória, será a mesma na Lua e na Terra.
III. O alcance horizontal máximo será maior na Lua.
IV. A velocidade com que o projétil toca o solo é a
mesma na Lua e na Terra.
2.
Relação entre as velocidades escalares médias
angular (ω) e linear (v).
3.
Movimento Circular e Uniforme
É todo movimento de trajetória circular em que a
velocidade escalar, linear ou angular, é constante e
diferente de zero.
I.
Período (T) e a frequência (f)
 Período (T) de um MCU é o intervalo de tempo decorrido
durante uma volta de uma dada partícula.
Está correta ou estão corretas:
OSG 1423/11
15
TC DE FÍSICA – 9º ANO – OLIMPÍADA
 Frequência (f) do movimento circular e uniforme executado
por uma partícula é o número de voltas que essa partícula
efetua por unidade de tempo.
Unidades:
Período
T=1s
T = 1 min
T=1H
b)
c)
d)
e)
ω1 = ω2 ‚ e v1 > v2.
ω1 > ω2 ‚ e v1 = v2.
ω1 > ω2 ‚ e v1 > v2.
ω1 < ω2 , e v1 < v2.
2.
Dois carros percorrem uma pista circular, de raio R, no
mesmo sentido, com velocidades de módulos constantes
e iguais a v e 3v. O tempo decorrido entre dois encontros
sucessivos vale:
a) π R/3v.
b) 2 π R/3v.
c) π R/v.
d) 2 π R/v.
e) 3 π R/v.
3.
Um móvel descreve um movimento circular uniforme
regido pela função horária do espaço S = 12 + 9t (S.I).
Se o raio da trajetória é 3 m, determine a função horária
do espaço angular para esse movimento.
4.
Uma esfera oca feita de papel tem diâmetro igual a 0,50 m
e gira com determinada frequência f0, conforme figura
adiante. Um projétil é disparado numa direção que passa
pelo equador da esfera, com velocidade v = 500 m/s.
Observa-se que, devido à frequência de rotação da
esfera, a bala sai pelo mesmo orifício feito pelo projétil
quando penetra na esfera. A frequência f0 da esfera é:
a) 200 Hz.
b) 300 Hz.
c) 400 Hz.
d) 500 Hz.
5.
Num toca fitas, a fita F do cassete passa em frente da
cabeça de leitura C com uma velocidade constante
v = 4,80 cm/s. O diâmetro do núcleo dos carretéis vale
2,0 cm. Com a fita completamente enrolada num dos
carretéis, o diâmetro externo do rolo de fita vale 5,0 cm.
A figura adiante representa a situação em que a fita
começa a se desenrolar do carretel A e a se enrolar no
núcleo do carretel B.
Frequência
f = r.p.s. = rot/s = 1 Hz (hertz).
f = r.p.m. = rot/min.
f = r.p.h. = rot/ h.
Velocidade Angular no MCU
Quadro de Resumo
4.
Transmissão de Movimento Circular Uniforme
4.1 Por Contato e Por Correia
Enquanto a fita é totalmente transferida de A para B, o
número de rotações completas por segundo (rps) do
carretel A:
a) varia de 0,32 a 0,80 rps.
b) varia de 0,96 a 2,40 rps.
c) varia de 1,92 a 4,80 rps.
d) permanece igual a 1,92 rps.
e) varia de 11,5 a 28,8 rps.
EXERCÍCIOS
1.
Sejam ω1 e ω2 as velocidades angulares dos ponteiros
das horas de um relógio da torre de uma igreja e de um
relógio de pulso, respectivamente, e v1 e v2 as velocidades
escalares das extremidades desses ponteiros. Se os dois
relógios fornecem a hora certa, pode-se afirmar que:
a) ω1 = ω2 ‚ e v1 = v2.
6.
16
A figura ao lado representa duas polias, 1 e 2, de raios
R1 e R2, sendo R1 < R2, interligadas por meio de uma
OSG 1423/11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
correia inextensível. Com relação a esse sistema,
podemos afirmar corretamente que:
a) 5
b) 7
c) 9
a) as frequências de rotação das duas polias são
iguais.
b) as velocidades angulares das duas polias são iguais.
c) o período da polia 2 é menor que o da polia 1.
d) a frequência da polia 2 é menor que a da polia 1.
e) a velocidade angular da polia 1 é igual a da polia 2.
7.
8.
9.
d) 11
e) 14
10. A figura mostra um carrossel girando com velocidade
constante. O cavalo B e o cavalo A encontram-se a 2 m e
3 m do centro, respectivamente. Determine a velocidade
angular de A, sabendo que a velocidade de B é de 3 m/s.
Duas polias, A e B, de raios R e R', com R<R', podem
girar em torno de dois eixos fixos e distintos, interligadas
por uma correia. As duas polias estão girando e a correia
não escorrega sobre elas. Então pode-se afirmar que
a(s) velocidade(s)
a) angular de A é menor que a de B, porque a
velocidade tangencial de B é maior que a de A.
b) angular de A é maior que a de B, porque a
velocidade tangencial de B é menor que a de A.
c) tangenciais de A e de B são iguais, porém a
velocidade angular de A é menor que a velocidade
angular de B.
d) angulares de A e de B são iguais, porém a
velocidade tangencial de A é maior que a velocidade
tangencial de B.
e) angular de A é maior que a velocidade angular de B,
porém ambas têm a mesma velocidade tangencial.
11. Considerar um ventilador com hélice girando. Em relação
aos pontos da hélice, é correto afirmar que
a) todos têm a mesma velocidade linear.
b) todos têm a mesma aceleração centrípeta.
c) os pontos mais afastados do eixo de rotação têm
maior velocidade angular.
d) os pontos mais afastados do eixo de rotação têm
menor aceleração centrípeta.
e) os pontos mais afastados do eixo de rotação têm
maior velocidade linear.
Pai e filho passeiam de bicicleta e andam lado a lado
com a mesma velocidade. Sabe-se que o diâmetro das
rodas da bicicleta do pai é o dobro do diâmetro das
rodas da bicicleta do filho. Pode-se afirmar que as rodas
da bicicleta do pai giram com
a) a metade da frequência e da velocidade angular com
que giram as rodas da bicicleta do filho.
b) a mesma frequência e velocidade angular com que
giram as rodas da bicicleta do filho.
c) o dobro da frequência e da velocidade angular com
que giram as rodas da bicicleta do filho.
d) a mesma frequência das rodas da bicicleta do filho,
mas com metade da velocidade angular.
e) a mesma frequência das rodas da bicicleta do filho,
mas com o dobro da velocidade angular.
12. A função horária angular de um movimento circular
uniforme, de raio 2 m, é ϕ = 10 + 4.t (S.I). A função
horária linear do movimento é:
a) s = 10 + 4.t
d) s = 100 + 16.t
b) s = 20 + 8.t
e) s = 10 + 8.t
c) s = 5 + 4.t
13. Na figura abaixo temos um móvel realizando um MCU. A
velocidade
linear
e
a
aceleração
apontam,
respectivamente, para os pontos:
a) 1 e 2
b) 4 e 1
c) 3 e 5
d) 2 e 6
e) 1 e 4
Em uma bicicleta, o ciclista pedala na coroa e o
movimento é transmitido à catraca pela corrente. A
frequência de giro da catraca é igual à da roda. Supondo
os diâmetros da coroa, catraca e roda iguais,
respectivamente, a 15 cm, 5,0 cm e 60 cm, a velocidade
dessa bicicleta, em m/s, quando o ciclista gira a coroa a
80 rpm, tem módulo mais próximo de
14. O comprimento do ponteiro dos minutos de um relógio é
1,5 vez o do ponteiro das horas. Sejam VM e VH as
velocidades tangenciais das extremidades dos ponteiros
dos segundos e das horas respectivamente. Então
encontre a relação VH / VM.
OSG 1423/11
17
TC DE FÍSICA – 9º ANO – OLIMPÍADA
15. Considere duas pessoas A e B, situadas sobre a
superfície da Terra, estando A no equador e B em um
paralelo no hemisfério norte (veja a figura deste
problema). Você sabe que estas pessoas estão girando,
juntamente com a Terra em seu movimento de rotação.
Dizer, entre as afirmações seguintes, relacionadas com
estes movimentos de rotação de A e B, qual a correta.
a) Qual a frequência de rotação do cilindro menor?
b) Qual a velocidade linear da cinta?
c) Determine a aceleração centrípeta de um ponto
situado na extremidade da polia 2.
19. Quem está na Terra vê sempre a mesma face da lua.
Isso ocorre porque:
a) a Lua não efetua rotação nem translação.
b) a Lua não efetua rotação, apenas translação.
c) os períodos de rotação e translação da Lua são
iguais.
d) as oportunidades para se observar a face
desconhecida coincidem com o período diurno da
Terra.
a) O período de rotação de A é maior do que o de B.
b) A velocidade angular de A é maior a de B.
c) O raio da trajetória de A é igual ao raio da trajetória
de B.
d) A velocidade linear de A é maior do que a de B.
e) A frequência de A é menor do que a de B.
20. Um disco de raio r gira com velocidade angular w
constante. Na borda do disco, está presa uma placa fina
de material facilmente perfurável. Um projétil é disparado
com velocidade v em direção ao eixo do disco, conforme
mostra a figura, e fura a placa no ponto A. Enquanto o
projétil prossegue sua trajetória sobre o disco, a placa gira
meia circunferência, de forma que o projétil atravessa
mais uma vez o mesmo orifício que havia perfurado.
Considere a velocidade do projétil constante e sua
trajetória retilínea. O módulo da velocidade v do projétil é:
16. Duas polias são ligadas por uma correia. Uma tem raio
40 cm e realiza 120 voltas por segundo. Calcule o
número de voltas por segundo realizada pela outra,
sabendo que tem 60 cm de raio.
a)
b)
c)
d)
e)
17. As bicicletas possuem uma corrente que liga uma coroa
dentada dianteira, movimentada pelos pedais, a uma
coroa localizada no eixo da roda traseira, como mostra a
figura. O número de voltas dadas pela roda traseira a
cada pedalada depende do tamanho relativo destas
coroas. Em que opção abaixo a roda traseira dá o maior
número de voltas por pedalada?
wr/
2wr/
wr/2
wr
w/r
21. A figura mostra um disco que gira em torno do centro O.
A velocidade do ponto X é 50 cm/s e a do ponto Y é de
10 cm/s. A distância XY vale 20 cm. Pode-se afirmar que
o valor da velocidade angular do disco, em radianos por
segundo, é:
a) 2,0
b) 5,0
c) 10,0
d) 20,0
22. Em
certo
dispositivo
mecânico,
esquematizado
parcialmente na figura, o movimento da roda A aciona as
rodas B e C, que possuem o mesmo eixo. Os raios das
rodas A, B e C valem 3,0 cm, 5,0 cm e 1,0 cm,
respectivamente. Sendo 30rpm a frequência da roda A,
pergunta-se:
18. Uma cinta funciona solidária com dois cilindros de raios
R1 = 10 cm e R2 = 60 cm. Supondo que o cilindro maior
tenha uma frequência de rotação f2 = 60 rpm, responda:
a) Em que sentido gira a roda C?
18
OSG 1423/11
TC DE FÍSICA – 9º ANO – OLIMPÍADA
b) Qual a frequência, a velocidade angular da roda C e a
velocidade linear de um ponto periférico dessa roda?
um orifício. Qual a velocidade angular do disco, em
rotações por minuto?
23. Um disco comum de vitrola gira com aproximadamente
30 rotações por minuto. Determine, para um ponto A
situado a 15 cm do centro do disco e para um ponto B
situado a 5,0 cm desse mesmo centro:
a) a frequência em hertz e o período em segundos;
b) a velocidade angular;
c) a velocidade linear.
24. Temos, na figura a seguir, duas polias A e B de raio RA e
RB, sendo RA = 20 cm e RB = 60 cm:
27. A figura mostra dois discos planos, D1 e D2, presos a um
eixo comum, E. O eixo é perpendicular a ambos os
discos e passa por seus centros. Em cada disco há um
furo situado a uma distância r do seu centro. Os discos
estão separados por uma distância d = 2,40 m e os furos
alinham-se sobre uma reta paralela ao eixo E. Calcule as
três frequências mais baixas (medidas em rotações por
segundo) com as quais deverão girar os discos se
quisermos que uma bala com velocidade v = 240 m/s,
que passa pelo primeiro furo, passe também pelo
segundo furo. Suponha a trajetória da bala paralela ao
eixo E.
A polia A gira com frequência igual a 1.200Hz, acionada
por um motor. A polia B também gira, acionada pela
polia A através do contato entre elas. Não há
escorregamento entre as polias na região de contato.
Determinar com que frequência a polia B gira.
28. Considere os pontos A, B e C, assinalados na bicicleta
da figura adiante.
25. Leia a tira abaixo
.
(MÁXIMO, Antônio & ALVARENGA, Beatriz. Curso de Física.
São Paulo: Harbra, 1992.)
A e B são pontos das duas engrenagens de transmissão
e C é um ponto externo do aro da roda. A alternativa que
corresponde à ordenação dos módulos das velocidades
lineares VA, VB e VC nos pontos A, B e C, é:
a) VB < VA < VC
b) VA < VB = VC
c) VA = VB < VC
d) VA = VB = VC
Calvin, o garotinho assustado da tira, é muito pequeno
para entender que pontos situados a diferentes
distâncias do centro de um disco em rotação têm:
a) mesma frequência, mesma velocidade angular e
mesma velocidade linear.
b) mesma frequência, mesma velocidade angular e
diferentes velocidades lineares.
c) mesma frequência, diferentes velocidades angulares
e diferentes velocidades lineares.
d) diferentes frequências, mesma velocidade angular e
diferentes velocidades lineares.
e) diferentes frequências, diferentes velocidades
angulares e mesma velocidade linear.
29. Duas polias, A e B, de raios RA e RB, respectivamente,
sendo RA = 3 RB, podem girar em torno de dois eixos
distintos e fixos, e interligadas por uma correia.
Sabendo-se que a polia A está girando a 60 rpm, e que a
correia não escorrega sobre as polias, determine a
frequência da polia B.
26. Uma arma dispara 30 balas/minuto. Estas balas atingem
um disco girante sempre no mesmo ponto atravessando
30. Duas polias, A e B, unidas através de um eixo rígido,
executam movimento circular uniforme, conforme mostra
a figura. Sabendo que VA = 10 m/s (velocidade da
OSG 1423/11
19
TC DE FÍSICA – 9º ANO – OLIMPÍADA
03.  = 4 + 3.t
04. D
05. A
06. D
07. E
08. A
09. B
10. 1,5 rad/s
11. E
12. B
13. B
14. 1/18
15. D
16. 80 voltas por segundo
17. A
18. a) 360 rpm
b) 1,2π m/s
c) 2,4π2 m/s2
19. C
20. B
21. A
22. a) anti-horário b) 18 rpm
23. a) 0,5 Hz e 2 s
b) π rad/s
c) 15π cm/s e 5π cm/s
24. 400Hz
25. B
26. π rad/s
27. 100Hz, 200Hz e 300Hz.
28. C
29. 180 rpm
30. 50 m/s
31. 10 voltas
32. F, V, V, V, F.
periferia da polia A) e que RB = 5 RA. Determine a
velocidade periférica da polia B.
31. Um disco gira num plano horizontal ao redor de um eixo
vertical que passa pelo seu centro, o disco efetua 300 rpm.
Solta-se uma pedra, do repouso e no vácuo, de uma altura
de 20 metros acima do disco, de tal modo que a pedra cai
sobre o disco. Quantas rotações terá efetuado o disco
desde o instante em que se solta a pedra até o instante
em que ela toca o disco? Considere g = 10 m/s2.
32. Duas polias, A e B, são ligadas por uma correia. A polia
A tem raio 2 R e gira no sentido horário com velocidade
angular A. A polia B tem raio R e gira com velocidade
angular B. O movimento de A é transmitido a B através
de uma correia. Não há escorregamento entre a correia
e as polias. Assinale (V) para verdadeiro e (F) para falso.
Referências Bibliográficas
DOCA, R.H.; BISCULA,G.J. e BOAS, N.V. Tópicos de Física, v.1,
Ed.18ª, Saraiva (2010).
(
(
(
(
(
) A = B
) Os pontos P e Q têm mesma velocidade linear v.
) A polia B gira no sentido horário.

) A  B
2
) A frequência da polia A é igual à frequência da
polia B.
JUNIOR,F.R.; FERRARO, N.G. e SOARES,P.A.T. Fundamentos da
Física, v.1, Ed 9ª. Moderna (2010).
33. A engrenagem A, acionada por um motor, gira com
velocidade angular A = 30 rad/s.
Sabendo que RB = 2RA e que RC = 1,5RA, determine os
sentidos de rotação e as velocidades angulares das
engrenagens B e C.
GABARTIO EXERCÍCIOS DE FIXAÇÃO
AULAS DE 14 A 16
01. B
02. C
Marcelo: 11-03-11 – Rev.:Nay
20
OSG 1423/11