Modelo de prova - Salesiano Dom Bosco

PARNAMIRIM - RN
Aluno(a):
Data: ____ / ____ / 2014
TRABALHO – MATEMÁTICA –FUNÇÃO LOGARÍTMICA E PROPRIEDADES DE LOGARITMO
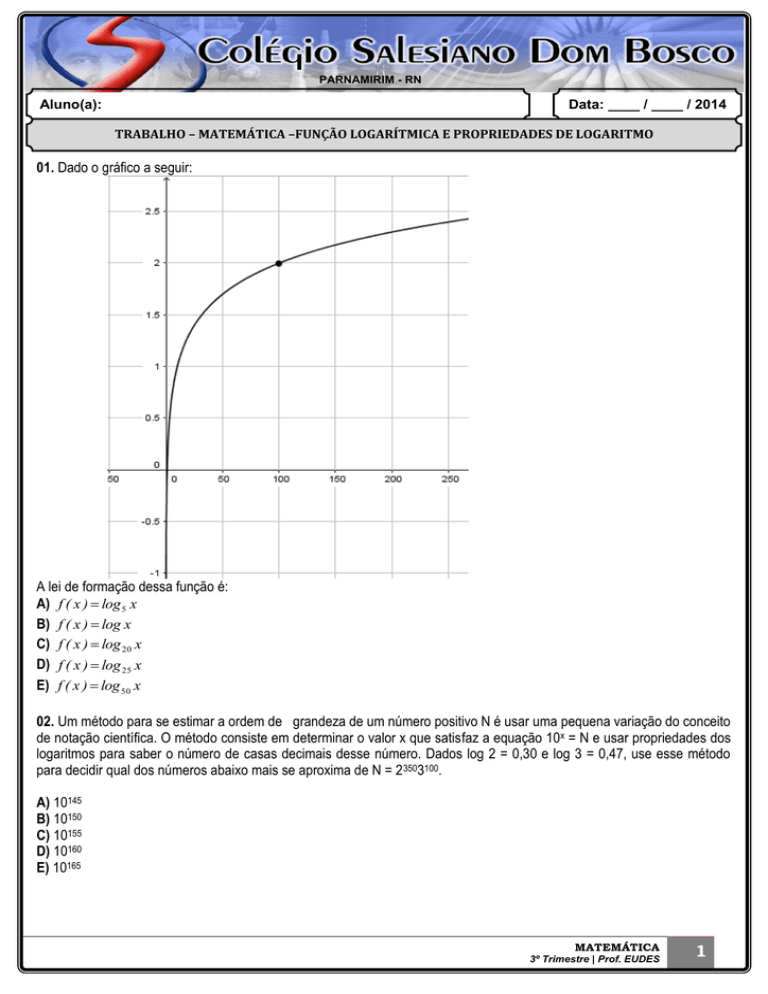
01. Dado o gráfico a seguir:
A lei de formação dessa função é:
A) f ( x )  log 5 x
B) f ( x )  log x
C) f ( x )  log 20 x
D) f ( x )  log 25 x
E) f ( x )  log 50 x
02. Um método para se estimar a ordem de grandeza de um número positivo N é usar uma pequena variação do conceito
de notação científica. O método consiste em determinar o valor x que satisfaz a equação 10x = N e usar propriedades dos
logaritmos para saber o número de casas decimais desse número. Dados log 2 = 0,30 e log 3 = 0,47, use esse método
para decidir qual dos números abaixo mais se aproxima de N = 2 3503100.
A) 10145
B) 10150
C) 10155
D) 10160
E) 10165
MATEMÁTICA
3º Trimestre | Prof. EUDES
1
03. O altímetro é o instrumento usado para medir alturas ou altitudes. Trata-se de um instrumento básico exigido para todas as aeronaves a receber certificado. Ele mede a pressão atmosférica e apresenta-a como altitude.
Suponha que a altitude h acima do nível do mar, em quilômetros, detectada pelo altímetro de um avião seja dada em
função da pressão atmosférica p , em atm, por A(p)  20  logp-1 .
Num determinado instante, a pressão atmosférica medida pelo altímetro era 0,4 atm. Considerando a aproximação
log2  0,3 , qual a altitude h do avião nesse instante, em quilômetros?
A) 4 km
B) 6 km
C) 8 km
D) 10 km
E) 12 km
04. Dado o gráfico a seguir:
Pode-se afirmar que a lei de formação da função representada no gráfico é:
A) f ( x )  log 3 x
B) f ( x )  log 4 x
C) f ( x )  log 6 x
D) f ( x )  log 1 x
3
E) f ( x )  log 1 x
6
05. Dado o gráfico a seguir:
Pode-se afirmar que a lei de formação da função representada no gráfico é:
A) f ( x )  log 2 x
B) f ( x )  log 4 x
C) f ( x )  log 8 x
D) f ( x )  log 1 x
2
E) f ( x )  log 1 x
8
MATEMÁTICA
3º Trimestre | Prof. EUDES
2
06. (UERJ) Dada à função logarítmica f definida por f(x)  log53 5 x2  então para x  25 temos:
A) f(x)  2
B) f(x)  3
C) f(x)  4
D) f(x)  5
E) f(x)  6
07. ( UEPG-PR ) Sendo log 2 = 0,30 e log 3 = 0,47, então log 60 vale:
A) 1,77
B) 1,41
C) 1,041
D) 2,141
E) 0,141
08. ( UFRGS ) A raiz da equação 2x = 12 é:
A) 6
B) 3,5
C) log 12
D) 2.log23
09. (UFRGS) A soma log  log  log  ........ log
2
3
4
19
3
4
5
20
A) – log 20
B) – 1
C) log 2
E) 2 + log23
é igual a
D) 1
E) 2
10. ( UFRGS – 08 ) A solução da equação (0,01)x = 50 é
A) – 1 + log 2
B) 1 + log 2
C) – 1 + log 2
D) 1 + log 2
E) 2 log 2
11. Dada a expressão A  ln e 2  3  ln 3 e  2  ln1 , o valor de A é:
A) -3
B) -2
C) -1
D) 0
12. Dada a expressão B  3
A) 1
B) 2
log3 2
E) 1
 2log2 3 , o valor de B é:
C) 3
D) 4
13. Qual é o valor de log9(log4 64) + log4 (log3 81)?
3
3
A) 1
B)
C)
D)  2
2
4
14. Qual é o valor de
?
8
11
A)  2
B)
C) 1
D)
3
5
E) 5
E) 0
E)
16
3
15. Se log E = 1 + log a + 2. log b – log c, então E é igual a:
A)
B)
C)
D)
E)
a10.b 2
c
a.b 2
1
c
10.a.b 2
c
10.a.c
b2
a10.c
b2
MATEMÁTICA
3º Trimestre | Prof. EUDES
3
16. As indicações R1 e R2 de dois terremotos, na escala Richter, estão relacionadas pela fórmula
R1- R2 = log (E1/E2)
em que E1 e E2‚ medem as respectivas energias, liberadas pelos terremotos em forma de ondas que se propagam pela
crosta terrestre. Nessas condições, se R1= 8,5 e R2= 7,0, é correto afirmar que a razão entre E1 e E2, nessa ordem, é igual
a:
A) 0,5
B) 1,5
C)10 0,5
D)10 1,5
E) 100
3
1
17. Considere os seguintes números reais: a  , b  log 3 3 e c  log3
. Então:
3
3
A) c  a  b
B) a  b  c
C) c  b  a
D) a  c  b
E) b  a  c
 1 

 a b 
18. Sejam a e b as raízes da equação x2  10 x  25  0 , o valor de log5 
A) -0,6
B) -1
C) -2
D) 1
E) 2
 1 

 ab
19. Sejam a e b as raízes da equação x2  16  48  0 , o valor de log2 
A) -4
B) -1
20. Resolvendo a equação
A) -6
B) -3
C) -2
3
0,5x
D) 2
 4 encontramos como solução:
C) -2
D) 4
é:
é:
E) 4
E) 8
MATEMÁTICA
3º Trimestre | Prof. EUDES
4