r1 corrente

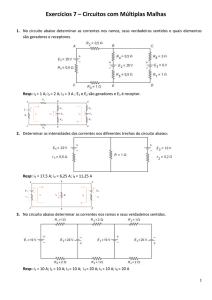
1. Um sistema trifásico alimenta um grupo de motores de 280kW com fator de potência
de 0,70 em atraso. O sistema possui capacidade nominal de 900kVA. Pede-se
1.1 – Qual deve ser a carga adicional que pode ser acrescentada, considerando
que a carga possui um fp igual a 0,9 indutivo, de forma que o sistema não fique em
sobrecarga.
1.2 – Após o item 1.1, defina qual o fator de potência total do sistema. Além
disto, calcule o banco de capacitores de forma a corrigir o fp para 0,92 em atraso.
Resp.: devemos fazer uma soma fasorial das potências. Lembrando que a potência
aparente é igual: P + j Q.
Muitos fizeram a soma escalar esquecendo-se do ângulo, representado no problema
pelo fator de potência. Enfim, não podemos somar duas potências aparentes com
ângulos diferentes sem ser pelo método fasorial.
2. Em um projeto, em que você foi convocado a opinar, duas opções foram propostas:
1ª. Condutor de 150 mm2, capacidade de 380 A, R=0,193 ohm/km – critério de
capacidade de corrente e 2ª. Condutor de 185 mm2, capacidade de 450 A, R=0,124
ohm/km – critério da secção econômica.
Considere que o tempo de utilização será de 5000 horas/ano, temperatura ambiente de
31oC, o comprimento do sistema é de 250m e corrente de projeto de 350A. Sabe-se que
a tarifa de energia é R$ 0,039/kWh e G´= 120. A relação entre n (Ib/Iz) e temperatura
de regime está tabela abaixo, onde os trechos podem ser aproximados por uma reta. É
fornecida também a tabela de correção de temperatura do cabo.
Considerando que o cabo de 150 mm2 custe R$ 11,50/km e o cabo de 185 custa
R$18,00/km e que o tempo analisado seja de 10 anos e a taxa de juros de 7% ao ano,
qual dos dois vc adotaria e por que?
Resp.: Aqui deve-se proceder um estudo investigativo sobre as duas condições
possíveis. Considerando o retorno ao longo do tempo, verificar qual dos dois é mais
vantajoso economicamente. Recomendo que se faça uma tabela comparativa para cada
uma das etapas de cálculo e, ao final, estabalecer qual o melhor investimento.
3. Para um determinado local as seguintes medições de campo pelo método de Wenner
foram obtidas. Efetue a estratificação do solo pelo método simplificado de duas camadas
determinando a resistividade aparente do solo, utilize (m = K2 * 1,5) Espaçamento a(m)
Resistividade Elétrica (ohms/m)
1
180
2
200
4
280
6
320
8
480
16
660
32
710
Considerando a haste com de 2,5m de profundidade e seção transversal de 380mm2,
calcule
3.1 - A resistência de aterramento com uma única haste;
3.2 - Faça nova simulação colocando hastes em paralelo, com espaçamento de 3 m
entre elas. Utilize 4 hastes. Qual o fator de redução na resistência de aterramento?
Resp.: Creio que este exercício não apresente grandes desafios aos futuros engenheiros.
A grande diferença com o que fizemos em sala é que o gráfico tem uma inclinação
positiva. No mais o mecanismo é o mesmo, ou seja, encontre rô1 e rô2, ache rôa e siga
em frente conforme os exercícios já resolvidos.
4. Considerando um sistema trifásico em que a amplitude (valores de pico) do sinal de
60Hz (fundamental) seja de 320A e a 3a harmônica seja de 60A e a 9a harmônica seja de
30A, calcule o valor da corrente total discretizando o sinal de 30 em 30 graus até atingir
os 180 graus da fundamental. Após isto, plote a curva contendo as três correntes mais a
resultante. Qual deve ser o valor da corrente de condutor de neutro?
Resp.: Discretizar os 180 graus da frequencia fundamental em 30 graus cada passo.
Observar que 30 graus da fundamental não são os mesmos 30 graus das harmônicas,
deve-se guardar as proporcionalidades. Feito isso, não tem mistério algum. Com os
pontos numa tabela, traçar as curvas solicatadas.
CEME
1. Calcule para o circuito em série-paralelo abaixo o valor da corrente I de forma que o
fluxo no entreferro seja de 2.10-4Wb. O núcleo é feito de aço laminado.
Resp.: A grande dica é analisar o sistema como um sistema elétrico e observar as leis dos
nós e das malhas. Assim, o ramo mais a direita possui dois módulos em série, do material
ferromagnético e o gap. Este ramo possui um ramo em paralelo, o bg. Feito isso, observe
que ainda temos um trecho inicial formado por ghab, onde todo o fluxo percorre o trecho.
2. Um transformador monofásico de 10 kVA, 13,8kV(primário)/220V(secundário)
apresenta a resistência do enrolamento primário R1 = 0,5Ω e a resistência do
enrolamento secundário R2 = 0,1Ω . A perda no ferro é 80 W.
2.1 O transformador alimenta no secundário, na tensão nominal, uma carga de 8
KVA, fator de potência 0,8 indutivo. Qual o rendimento do sistema supondo que o
mesmo esteja alimentado com uma fonte ideal?
2.2 Supondo um regime de carga diário mostrado abaixo, qual é o seu
rendimento diário? (considere fp = 1)
6h – plena carga; 6h – meia-carga; 4h – 1,25 plena carga; 2h – a vazio; 6h – 2/3 da
plena carga
Resp.: Todos sabemos que as perdas no trafo são cobre e ferro, sendo que as do ferro
são constantes e foram dadas. No entanto, as perdas no cobre são função da corrente
que passa pelos condutores ou enrolamentos, sendo eles primário e secundário. Sendo
assim, é necessário calcular qual é a corrente que está passando pelo condutor
(primário e secundário) na condição de carga estabelecida. Depois disso, é só a aplicar a
equação que estabelece as perdas por efeito joule.
Sob o mesmo mecanismo é possível achar as perdas nominais, sendo para isto
aplicando a carga nominal ao trafo.
3. Um motor série de 40 cv, 120 V, 900 rpm, tem rendimento de 90 % a plena carga.
Nestas condições, a queda de tensão em Rs é 10,0 % da queda de tensão em Ra.
Considere 1cv = 736W e determine:
3.1. A corrente de armadura, a resistência da armadura (Ra) e a resistência do campo
série (Rs).
3.2. O conjugado de partida.
3.3. O reostato de partida de modo que a corrente na partida seja igual a 2 vezes a
nominal.
Resp.: Para iniciarmos o processo precisamos desenhar o esquema elétrico do motor
série. Teremos então a idéia de como as tensões e correntes se desenvolvem em cada
resistência (série e armadura). O rendimento informa a relação de potência de saída e a
potência de entrada. Com a diferença, é possível mensaurar a corrente que o motor
puxa da rede e que passa pelo circuito da armadura.
Na partida, não há Ec, logo a corrente tende a subir. Para isto precisamos limitar com
reostatos, que devem ser projetados com a corrente máxima permissível, no caso 2
vezes a nominal.
4. Um gerador cc shunt (12kW, 100V, 1000 rpm – dados da armadura) tem Ra = 0,1 Ω
e Rf = 80 Ω. Os dados da curva de magnetização são fornecidos abaixo para n =
500rpm.
If(A) 0,2 0,4 0,6 0,8 1,0 1,2 1,4
Eg(V) 15 31 40 45 50 52,5 56
Pede-se:
4.1 – A máxima tensão gerada a vazio em 1000 rpm;
4.2 – A resistência crítica de campo.
4.3 – Considerando que o gerador alimenta a carga nominal em 1000rpm, qual deve ser
o valor do reostato de campo a ser inserido de forma que exista um ponto de operação
dentro das características da curva de magnetização? (considere que a Tensão gerada é
100V)
Resp.: A curva foi levantada para uma velocidade de 500 rpm, e a questão foi elaborada
com 1000 rpm. Assim, devemos traçar a curva usando a equação que ajusta a tensão
conforme a velocidade, observe que a curva é em vazio, logo não há influência da
carga.
A resistência crítica de campo é o valor de resistência em que não é possível autoexcitar a máquina a vazio. Ou seja, uma reta tangente a curva de magnatização.
Sob a curva de magnetização, qual deve ser o valor de Rf sob uma carga nominal, ou
seja, com Ia conhecido, considerando um ponto existente sob a curva de magnetização.