mat3_aula7

Visualização do documento
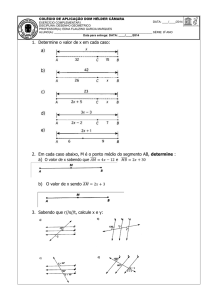
mat3_aula7.doc
AULA
(85 KB) Baixar
Matemática 3
7
Polígonos Convexos
1
1. DEFINIÇÃO
Trata-se de uma linha poligonal onde a extremidade do ponto inicial coincide com o ponto final.
Pode-se dividir ainda em polígonos entrelaçados e não-entrelaçados.
a ) Polígono entrelaçado
Os segmentos do polígono se cruzam entre si.
b ) Polígono não entrelaçado
Podem ser subdivididos em duas classes: Côncavos e convexos.
2. POLÍGONOS CÔNCAVOS
São polígonos onde é possível escolher dois pontos internos ao polígono e este mesmo segmento de reta passar por fora do
polígono.
3. POLÍGONOS CONVEXOS
São polígonos onde não é possível encontrar um segmento de reta que passe por fora do polígono.
4. ELEMENTOS BÁSICOS
Seja um polígono convexo dado pela figura abaixo.
Assim:
A, B, C, D, E, F são os vértices
são os lados
são as diagonais
â1, â2, ....., ân são os ângulos internos
Â1, Â2, ...., Ân são os ângulos externos
5. PROPRIEDADE IMPORTANTE
“ Os ângulos interno e externo de qualquer ponto de qualquer polígono convexo são suplementares ”, ou seja:
6. SOMA DOS ÂNGULOS INTERNOS DE POLIGONOS CONVEXOS
“ A soma dos ângulos internos de qualquer polígono convexo é função do número de lados que o mesmo possui. ”
7. SOMA DOS ÂNGULOS EXTERNOS DE POLIGONOS CONVEXOS
“ A soma dos ângulos externos de qualquer polígono convexo é sempre igual a 360 º. “
8. POLÍGONOS REGULARES
São polígonos onde os lados são iguais (eqüilátero) e os ângulos também iguais (eqüiângulo).
OBS: Para polígonos regulares temos que:
9. NÚMERO DE DIAGONAIS DE UM POLIGONO CONVEXO
10. NÚMERO DE DIAGONAIS QUE PASSAM PELO CENTRO DE UM POLIGONO CONVEXO
“ Para se ter diagonais que passam pelo centro é necessário ter um número par de lados, pois o polígono deve ser simétrico. “
Número de
lados
Passam
pelo
centro
2k ( par )
n/2
2k+1 ( ímpar )
0
Não passam
pelo centro
Total de
diagonais
EXERCÍCIOS
1. Calcule a soma dos ângulos internos de um decágono convexo.
2. Determine o polígono cujo número de lados é igual ao número de diagonais.
3. Qual a medida mais próxima de cada ângulo externo do heptágono regular da moeda de R$ 0,25 ?
4. Qual o polígono regular cujo ângulo interno mede o triplo do ângulo externo?
5. Dois ângulos internos de um polígono convexo medem 130º cada um e os demais ângulos internos medem 128º cada um.
Qual o número de lados do polígono em questão?
6. Num polígono regular o ângulo interno excede o externo de 108º. Calcule o número de diagonais distintas do polígono.
7. A razão entre o número de diagonais de dois polígonos é 5/26. Um deles possui o dobro do número de lados do outro. Determine
esses polígonos.
8. Num polígono, a soma dos ângulos internos adicionada à soma dos ângulos externos é igual a 1440º. Determine o número de
diagonais do polígono.
9.
polígono.
são dois lados consecutivos de um polígono regular. Se
10. Considere um hexágono regular ABDDEF e um quadrado externo ABGH. Calcule os ângulos:
achar o número de lados do
RESPOSTAS:
1 ) Si = 1440 º
2 ) pentágono
3 ) 51 º
4 ) octógono
5)7
6 ) 35 diagonais
7 ) octógono e hexadecágono
8 ) 20 diagonais
9 ) 5 lados
10 )
Arquivo da conta:
cacic.ensino
Outros arquivos desta pasta:


mat3_aula1Will.doc (410 KB)
mat3_aula2Will.doc (287 KB)
 mat3_aula3.doc (1558 KB)
 mat3_aula4.doc (75 KB)
 mat3_aula5.doc (68 KB)
Outros arquivos desta conta:





Bio 01
Bio 02
Bio 03
Fis 01
Fis 02
Relatar se os regulamentos foram violados



Página inicial
Contacta-nos
Ajuda





Opções
Termos e condições
Política de privacidade
Reportar abuso
Copyright © 2012 Minhateca.com.br