Curso: ENGENHARIA BÁSICA DP - DINÂMICA DO SÓLIDO LISTA

Curso: ENGENHARIA BÁSICA
DP - DINÂMICA DO SÓLIDO
LISTA DE EXERCÍCIOS – (B1)
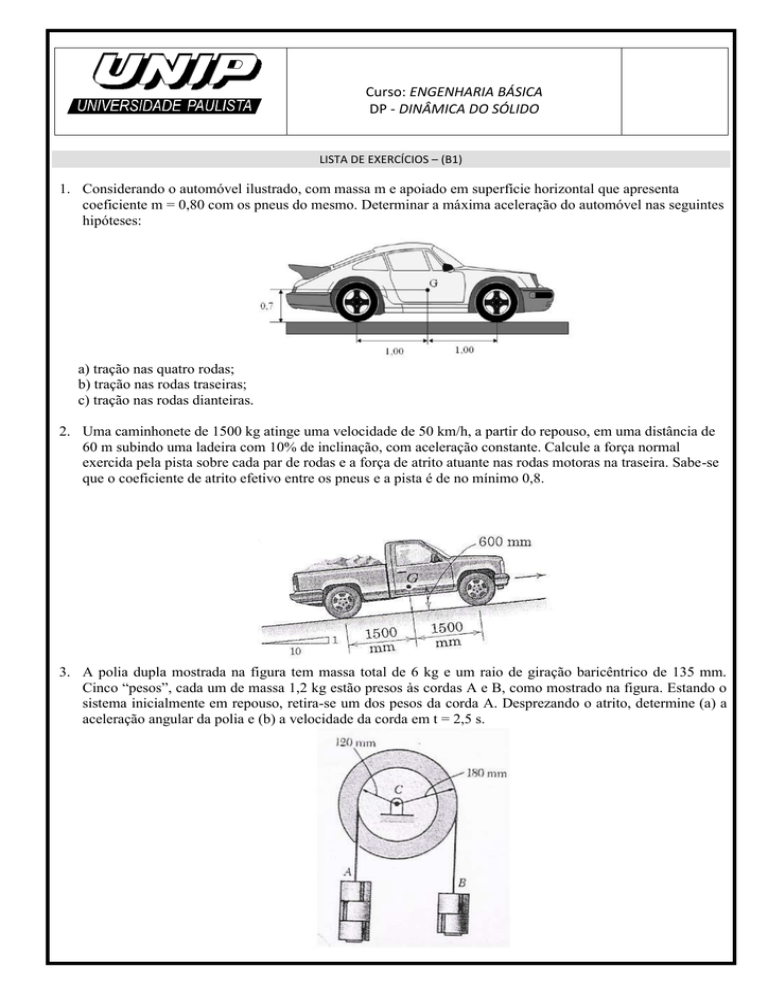
1. Considerando o automóvel ilustrado, com massa m e apoiado em superfície horizontal que apresenta
coeficiente m = 0,80 com os pneus do mesmo. Determinar a máxima aceleração do automóvel nas seguintes
hipóteses:
a) tração nas quatro rodas;
b) tração nas rodas traseiras;
c) tração nas rodas dianteiras.
2. Uma caminhonete de 1500 kg atinge uma velocidade de 50 km/h, a partir do repouso, em uma distância de
60 m subindo uma ladeira com 10% de inclinação, com aceleração constante. Calcule a força normal
exercida pela pista sobre cada par de rodas e a força de atrito atuante nas rodas motoras na traseira. Sabe-se
que o coeficiente de atrito efetivo entre os pneus e a pista é de no mínimo 0,8.
3. A polia dupla mostrada na figura tem massa total de 6 kg e um raio de giração baricêntrico de 135 mm.
Cinco “pesos”, cada um de massa 1,2 kg estão presos às cordas A e B, como mostrado na figura. Estando o
sistema inicialmente em repouso, retira-se um dos pesos da corda A. Desprezando o atrito, determine (a) a
aceleração angular da polia e (b) a velocidade da corda em t = 2,5 s.
4.
O tambor de 60 mm de raio está ligado a um disco de 120 mm de raio. O disco e o tambor têm uma massa
total de 6 kg e um raio de giração combinado de 90 mm. Liga-se uma corda como se mostra na figura e
puxa-se com a força de 20 N. Sabendo que o disco rola sem escorregar, determine (a) a aceleração angular
do disco e a aceleração de G e (b) o mínimo valor do coeficiente de atrito estático compatível com o
movimento.
5. Uma corda está enrolada num disco homogêneo de raio r = 0,50 m e massa m = 15 kg. Se a
corda for puxada para cima com uma força T de módulo igual a 190 N, determine:
A. A aceleração do centro do disco;
B. A aceleração angular do disco;
C. A aceleração da corda.
6. Uma corda está enrolada no tambor interno de uma roda e é puxada horizontalmente com uma
força de 200 N. A roda tem massa de 50 kg e raio de giração de 70 mm. Sabendo-se que µE =
0,20 e µC = 0,15, determine a aceleração de G e a aceleração angular da roda.
OBS.: Para a resolução da questão suponha um rolamento com escorregamento.
7.
Um aro metálico com raio r = 150 mm é liberado do repouso sobre a ladeira com 20° de inclinação.
Se os coeficientes de atrito estático e dinâmico são μe = 0,15 e μc = 0,12, determine a aceleração
angular α do aro e o tempo t para que ele se mova de uma distância de 3 m ladeira abaixo.
8. Uma esfera de raio r e peso P é liberada com velocidade inicial nula sobre um plano inclinado e
rola sem escorregar. Determine:
A. O valor mínimo do coeficiente de atrito compatível com o movimento de rolamento;
B. A velocidade do centro G da esfera após ter rolado 3,0 m.
9. Um armário com 30 kg é montado sobre rodas que permitem o seu movimento livre sobre o
pavimento. Se for aplicada uma carga de 150 N como se mostra na figura, determine:
A. a aceleração do armário;
B. a gama de valores de h para os quais o armário não tomba.
10. Uma placa circular de raio r e massa m está suspensa por dois fios da massas desprezíveis como
é mostrado. Se o fio B se partir, determine a aceleração neste instante.
A. Do ponto A;
B. Do ponto B.
11. A barra vertical AB possui uma massa de 150 kg e seu centro de massa G está no ponto médio entre
suas extremidades. A barra é elevada do repouso em θ = 0 por meio de um mecanismo de hastes
paralelas, cujas massas são desprezíveis, com um momento constante M = 5 kN.m aplicado à haste
inferior no mancal C. Determine a aceleração angular α das barras em função de θ e obtenha a força
B na haste DB no instante em que θ = 30°.
12. Um disco A de massa de 6 kg e velocidade angular inicial de 360 rpm no sentido horário. O disco B tem uma
massa de 3 kg e está inicialmente em repouso. Os discos são colocados em contato entre si, pela aplicação
de uma força horizontal de 20 N sobre o eixo do disco A. Sabendo que µc = 0,15 entre os discos e
desprezando o atrito nos apoios, determine (a) a aceleração angular de cada disco e (b) a velocidade angular
final de cada disco.
13. O bloco de concreto de 300 kg é elevado pelo mecanismo de içamento mostrado na figura, onde os
cabos são enrolados sem folga em torno dos respectivos tambores. Os tambores, que são unidos e
giram como um conjunto único em torno do seu centro de massa em O, possuem uma massa
combinada de 150 kg e um raio de giração de 450 mm em relação a O. Se uma força de tração
constante P de 1,8 kN é mantida pela unidade de potência em A, determine a aceleração vertical do
bloco e a força resultante sobre o mancal em O.
14. O extremo A da barra uniforme AB com massa de 8 kg está ligado a um cursor que pode deslizar sem atrito
numa barra vertical. O extremo B da barra está ligado a um cabo vertical BC. Se a barra for libertada do
repouso na posição mostrada, determine (a) a aceleração angular da barra e (b) a reação em A.
15. Ao tambor A é imposta uma aceleração angular constante ao de 3 rad/s 2, que faz com que o carretel B
de 70 kg role sobre a superfície horizontal. O tambor A aciona o carretel B por meio do cabo de
conexão, que se enrola em volta do centro do carretel. O raio de giração do carretel, em relação ao
eixo que passa pelo seu centro de massa G, é de 250 mm, e o coeficiente de atrito estático entre o
carretel e a superfície horizontal é de 0,25. Determine a força trativa T atuante no cabo e a força de
atrito F exercida pela superfície horizontal sobre o carretel.