d = 1, .0,4 = O,6km (segunda

Um rio de Ikrn de largura tem uma correnteza
1,5 km/h.
de velocidade
Um homem atravessa o rio de barco, remando a uma
de 2,5 krn/h em relaçào a água. a) Qual é o tempo mínimo que leva para atravessar
velocidade
o rio? Onde desembarca
nesse
CêlSO?
b) Suponha agora que o homem quer chegar a um ponto diametralmente
forma a atingi·lo
diretamente,
remar numa direção
Oll
perpendicular
oposto na outra margem,
a margem
sendo arrastado
ponto onde quer chegar. e depois caminha de volta até lá. Se ele caminha a 6 km/h,
e tem duas opções
pela correnteza
: remar de
até além do
qual das duas opções e mais vantajosa.
e
quanto tempo leva?
Resposta
a) 24 mio: 600 m adiante;
d ==
a)
b) tanto faz: 30 min
lJ.t
1:;;::
:2,5.t
t:;;::
O,4h
= 24min
b) para chegar exatamente
remar para a diagonal,
2 tirei -
Com Pitágoras:
no ponto onde ele quer (que fica exatamente
certo? Desenhando os vetores velocidade
2
tl
corr
e como há uma correnteza,
ficaremos
com um triângulo
ele deve
retângulo.
. 2
-t-tl
res
= 2,SL
·v2res
na sua frente).
relativa e de correnteza,
1,52 =
Y4- = 2
Então:
1=2.t
t=0,5h= 30min
O outro jeito
é remar
Sabemos também
perpendicularmente
que, pelo princípio
é levado para percorrer
e voltar
na horizontal.
Esse princípio
vetor encontraremos
seja, a velocidade
mesmo que levaria
é um
resultante
para atravessar
(ocorrem
A velocidade
relativa
composto,
do barco
é
(movimento
movimento
quanto ele deve caminhar:
cada um dos componentes
na dtagonal,
relativo)
composto.
O mesmo acontece.
a sua velocidade
em relação
à
margem
que
em relação
é
a velocidade
e outro na horizontal
Isso significa
sem, pois um componente
ao mesmo tempo).
é a sua velocidade
perpendicularmente
d
ele leva 24min.
= 1, .0,4 = O,6km
ele levou 0,1 h=6min para chegar ao destino caminhando.
No caso, temos um movimento
um vetor na vertical
simultâneos
à
a õkm/h,
que remando
o mesmo tempo que ele leva para percorrer
é
na -ertical
(segunda
Somando 6min +
tanto faz o caminho escolhido.
diz que, quando há um movimento
demais nào existissem.
arrasto)
Portanto
Já calculamos
dos movimentos,
Então podemos calcular
resposta da letra a). Como ele caminhou
24min remando=30min.
caminhando.
da simultaneidade
desse movimento
resultante,
(movimento
que o tempo para atravessar
nào interfere
no movimento
do outro.
no lançamento
horizontal
à
água (vetor vertical,
E o movimento
o rio. com correnteza.
ou
é o
E ambos os componentes
sào
no vácuo.
no caso). A velocidade
resultante
este
de arrasto ou da correnteza),
por exemplo,
(vetor horizontal).
se realiza como se os
certo? Se decompormos
da correnteza
é a velocidade
(ou
do barco em relação
margem (díagonal).
2,5 é a velocidade
do veto r velocidade
relativa
relativa,
e 1,5 é a velocidade
já que o de arrasto,
de arrasto.
A resultante
nesse caso, não muda.
(soma vetorial
dessas duas) depende do sentido e direção
......
Universidade Federal do Rio Grande do Sul
Física 1e (Turma N) - fis01181
Prova 1
Semestre: 2016/2
Data: 21/10/2016
Prof.: Ricardo MeIo Ferreira
____
c; \J ,'8O
Nome:
90f-,c
fjk= 0Vv\Jl%.Q
Cartão -Ld""'-"olIJ),-Y.->-=l_i.{..L?......,..'
_
3/ '27
Nota
As respostas devem estar a caneta e conter as unidades sempre que for o caso.
1r Zh
fl,
II
1. Um rio de 1 km de largura tem uma correnteza de velocidade 1,5 km]h: Um homem atravessa o rio de
remando à uma velocidade de 2, 5 km/~m relação à água.
(a) Qual o tempo mínimo que leva para atravessar o rio? Onde desembarca nesse caso? f.::d)/l(
h
bE,l'C:I.
X=~(V
RtU1
(b) Suponha agora que o homem quer chegar a um ponto diametralmente oposto na outra margem, e tm.:
duas opções: remar de forma a atingi-Ia diretamente, ou remar numa direção perpendicular à margv»
sendo arrastado pela correnteza até além de onde quer chegar, e depois caminhar de volta até lá. Se <:;..
caminha a 6 kmJh qual das duas opçõest
.f(;ntJ.CYl.
NIJ"ft'~"
~ ~I
.
dJ'~cp:
\f
n
x-:
-
\f k(
----"
I
I
Ir
-=.
\(
,
c2 S
o ::
L~tQ -
\ C....,
I S' ~~/~
e""",,tA -
!j\.
~ro
mai~A,Y~~~~~ e quaIl}jotem~o lev!f~
fJ1Jl/~
c.o
v(t'f'<UVUA
h
J j -~
1
I
.-J
'S' ~~
l.
t -)
'1
<; )~""i '
J~
to
~/WII
",'~f"'h".
<iQ (j)
I -t
,iI
V
/
)L
J(
\Jyt1r
s@~,'1
X- ::. aJ I\{ --RItV\
tc : ~ xrSJ,2f
3.s X @ 2. 8'
----jl
')( ::. 1), '3 J- ~.
c~
I
I
-=-
I
I
_--'----l
\ I,
'\
G~),-~s~i::
FísicVC
O,.Tia
(Turma N) - fis01181
Prova 1 Página 2 de 4
21/10/2016
figura um bloco de massa mj ~ 1, O kg sobre um plano inclinado sem atrito está ligado a um bloco suspenso
de massa m2 = 2, O kg. A polia tem massa e atrito desprezíveis. Uma força vertical de módulo F ~ 6,00 N
atua sobre o bloco suspenso, que tem uma aceleração para baixo de 5,5 m/ 82. Determine a tensão na corda e
o ângulo (3.
(YIn ( ""; )
I
o)
{õYlJ- ~ ~,t9-
Tx,=-T~p
~"":-T~p
v.--- ----_.--
~
õ
{tr
FiS~(TUrma
N) - fis01181
Prova 1 Página 3 de 4
-1Ia. ~oco
21/10/2016
e
de massa m está sobre um plano com inclinação
conforme a figura. () coeficiente de atrito estátiu:
entre o bloco e o plano é /-te. Uma força gradualmente crescente puxa para baixo a mola, de constante de força
k. Encontre a energia potencial da mola em função de m, e, /-te e k no momento em que o bloco começa a se
mover.
r:n~ffn1
. .
~
\)
VJa>-.~~ -
L
}{JC2-=c
BUlZ. ~
ryn
J~.
~~cvfdeh~
cJ-
= 'Yn V
}r x:
I
~
/Wl~V'-::;
r:
.
k/'::.
,02
I
ml1
#-~- '
cL
-x:
.
\'
/'"
J
~ Jí:~l_
~:,7}1'YV
I~ .
.R~9"f'~
CA~j)
=» ~
f r;c
VI
2-
2) Um bloco de massa m está em repouso sobre um plano inclinado, como mostrado na figura abaixo. O
coeficiente de atrito estático entre o bloco e o plano é ue, Uma força gradualmente crescente puxa para
baixo a mola ( de constante de força k). Detemune a energia potencial U da mola (em termos dos dados)
jmg('inll • JI. <0,/1))'
no momento em que o bloco começa a se mover. R: U-
2J;
/:'
J:j
'. "t
".'
~,
s'
.
.
'.'.
3) O bloco de 2,0 kg desliza para baixo, ao longo de uma rampa curva sem atrito, partindo do repouso de uma altura
de 3,0 m. O bloco desliza, então, por 9,0111,ao longo de uma superfície horizontal rugosa antes de atingir o
Ffsica.LC (Turma N) - fis01181
Prova 1 Página 4 de 4
21/10/2016
Uma partícula tem uma velocidade inicial vo. Ela colide com uma segunda partícula de mesma massa, que está
inicialmente em repouso. A primeira partícula é defletida de um ângulo </>. Sua velocidade, após a colisão, é v.
segunda partícula recua e sua velocidade forma um ângulo
com a orientação original da primeira partícula.
e
Mostre que tane =
(b
Mostre que, se a colisão é elástica, então v = Vo cosdi
-- .JJ
~8
\[ tO-N'
v senp
vo+v cosd:
tu-
aftv'\
VCO)
\Je
--\lI
8
lOJV\~
L
-:i.(- -~1
~
eU)
e
"
Universidade Federal do Rio Grande do Sul
I As respostas
U-
Nome: (;'\1,'1)0
Física 1C (Turma N) - fis0118i
Teste 1
Semestre: 2016/2
Data: 26/08/2016
Prof.: Ricardo Meio Ferreira
Cartão
Nota
(?AM4a..G,.o
~-h'iVt
c2. ()) ~ ,2 Li g'
~{7
devem estar a caneta e conter as unidades sempre que for o caso.
II
1. Em um circo pretende-se realizar um truque disparando-se duas bolas com um canhão de ar e fazendo-as colidir
no ar. Para realizar o truque um atirador dispara a primeira bola formando 60° com a horizontal. Três segundos
depois ele dispara a segunda bola, formando 30° com a horizontal. Sabendo que as duas bolas se chocam no
ar, e que o canhão dispara sempre com a mesma velocidade V, determine:
6 8,~IWlI /)
bola voa antes de ser atingida. '3 (~~
(a) Qual a velocidade de lançamento do canhão;
~.- --------~~,:~~l
(b) Quanto tempo a primeira
hNV\~x-" V=<J>
'
-~-----
~~
/
-:
~
,Z~~~~
~
o
--;>
\J!;L -::
,--
'\ \r
\J ~~
-'
\ ~OJ
c
\ \)0 ~
l-- f
1), ~~;;
\I,
VtJ ~
{j),.{
\,
---rI
.
~
G -::'3 (Do
\JO~,
\J.
O
ICS) ê)ú>" ('t)
ú
ftQM
3({)
J
cL-----
~~:c~
I~( ~
~67-~
h ~ (o
I
'v=
\J -:-
I~
lD -:: \}
i)
A
-
~
OJ
y~
,0
1:
h -
t9 ~
c:)
I
D
t
f
\
\1 2, -= ~
0
\\Jo
s
-=
'I
6l ;-
\J(t
Vg:C
~
6
:
~CO (
\),6 D, S- '3, K
\JOg
~ff
V{3
rJ ,J'(pc, .
(f
t'!J tYi)/1) V~ \ \JOít
O-
\J.J
líH'6' ",,11) VIS
9J:-
6
b
Universidade Federal do Rio Grande do Sul
Física
le
Nome: ~~~
(Turma N) - fis01181
Teste 2
Semestre: 2016/2
Data: 26/09/2016
Prof.: Ricardo MeIo Ferreira
__ ~~~
g-=-
Cartão ---.::OW-==-----'l('---=L=--'-l...•....
Nota
~/a:J
_
_
As resposta ..",devem estar a eaneta e t:onter as unidades sempre que for o caso.
II
1. Uma corda é usada para subir verticalmente um bloco de massa M inicialmente em repouso, com uma aceleração
constante para cima de módulo gj4. Após o bloco subir uma distância d, determine, sern utilizar equações
da cinemática:
(a) o trabalho realizado pela força da corda sobre o bloco;
(b) o trabalho realizado pela força gravitacional sobre o bloco;
(t:) a energia cinética do bloco;
(d) a velocidade do bloco.
~
eo(l..C P\
J~"
W'
o.
1,
[\N-Fxkl~
-
~/
9~~;~~~cÁ-J
V}--
(l7lX~
~
~GcL
~-
f{ -=- ~
Cd~
(} Ad. ')
a.
""'~
\IV -c,
I~--..,...,.""",,",""-
---
~-A-(r->~)
-:
I." _
1.?.l (<'J
pMI 9
H-é};L
U
k~ ~ C()
'JQN\G
'C
fj
.óJ )
Acl)
2/.
21 de Novembro
LISTA 3 - Prof. Jason Gallas, DF-UFPB
7
Trabalho e Energia Cinética
~ (a) A força aplicada é constante e o trabalho feito por
ela é
WF = F· d = Fâcce o,
WF
As molas A e B são idênticas, exceto pelo fato de que A
é mais rígida do que B, isto é kA > k». Qual das duas
molas realiza um trabalho maior (a) quando elas sofrem
o mesmo deslocamento e (b) quando elas são distendidas por forças iguais.
~ (a) Temos WA = kAx2/2 e WB = kBx2/2, onde x
representa o deslocamento comum a ambas molas. Portanto,
WA _ kA
1
WB - kB > ,
ou seja, WA
= kAXA/kB.
Portanto
kAX'1.
kB(kAXA/kB)2
=
kB
kA < 1,
< WB.
7.2 Problemas e Exercícios
7.2.1 Trabalho:
stante
I E 7-2
movimento 1D com força con-
(7-7/6a edição)
=
(210) (3) cos 20°
(???/6a)
Para empurrar um caixote de 50 kg num piso sem atrito,
um operário aplica uma força de 210 N, dirigida 20°
acima da horizontal. Se o caixote se desloca de 3 m, qual
o trabalho executado sobre o caixote (a) pelo operário,
(b) pelo peso do caixote e (c) pela força normal exercida pelo piso sobre o caixote? (d) Qual o trabalho total
executado sobre o caixote?
http://www.fisica.ufpb.br/~jgallas
590 J.
I
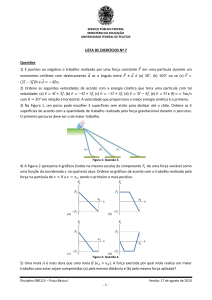
A Fig. 7-27 mostra um conjunto de polias usado para
facilitar o levantamento de um peso L. Suponha que o
atrito seja desprezível e que as duas polias de baixo, às
quais está presa a carga, pesem juntas 20 N. Uma carga
de 840 N deve ser levantada 12 m. (a) Qual a força
mínima F necessária para levantar a carga? (b) Qual o
trabalho executado para levantar a carga de 12 m? (c)
Qual o deslocamento da extremidade livre da corda? (d)
Qual o trabalho executado pela força F para realizar esta
tarefa?
~ (a) Supondo que o peso da corda é desprezível (isto é,
que a massa da corda seja nula), a tensão nela é a mesma
ao longo de todo seu comprimento.
Considerando as
duas polias móveis (as duas que estão ligadas ao peso
L) vemos que tais polias puxam o peso para cima com
uma força F aplicada em quatro pontos, de modo que a
força total para cima aplicada nas polias móveis é 4F.
Se F for a força mínima para levantar a carga (com velocidade constante, i.e. sem acelera-Ia), então a segunda
lei de Newton nos diz que devemos ter
= O,
4F -Mg
I
=
(b) A força da gravidade aponta para baixo, perpendicular ao deslocamento do caixote. O ângulo entre esta
força e o deslocamento é 90° e, como cos 90° = O, o
trabalho feito pela força gravitacional é ZERO.
(c) A força normal exercida pelo piso também atua perpendicularmente
ao deslocamento, de modo que o trabalho por ela realizado também é ZERO.
(d) As três forças acima mencionadas são as únicas que
atuam no caixote. Portanto o trabalho total é dado pela
soma dos trabalhos individuais realizados por cada uma
das três forças, ou seja, o trabalho total é 590 J.
I P 7-9
ou seja, WA > WB.
(b) Agora temos WA = kAx'1./2 e WB = kBX1/2,
onde XA e XB representam os delocamentos provocados
pela força idêntica que atua sobre ambas as molas e que
implica ter-se, em magnitude,
WA
WB
às 22:55
onde F é a força, d é o deslocamento do caixote, e cp é
o ângulo entre a força F e o deslocamento d. Portanto,
7.1 Questões
donte tiramos XB
de 20l3,
onde M 9 representa o peso total da carga mais polias
móveis, ou seja, Mg = (840 + 20) N. Assim, encontramos que
F
=
860
4
=
215 N.
(b) O trabalho feito pela corda é W = 4F d = M gd,
onde d é a distância de levantamento da carga. Portanto,
o trabalho feito pela corda é
W
=
(860)(12)
=
10320 J.
Página 2 de 7
LISTA 3 - Prof. Jason Gallas, DF-UFPB
(A resposta na tradução do livro está incorreta.)
(c) A cada metro que a carga sobe, cada segmento
da corda entre o conjunto superior e inferior de polias
diminui de um metro. Ou seja, a extremidade livre da
corda abaixo de 4 metros. Portanto, no total a extremidade livre da corda move-se (4)(12) = 48 m para baixo.
(d) O trabalho feito pela pessoa que puxa a corda pela
extremidade livre é W = Fd = Mgdj4, onde d é a
distância que a extremidade livre se move. Portanto,
W
= (860) ~ = 10320 J.
Observe que os valores encontrados nos itens (b) e (d)
devem coincidir, o que não ocorre com as respostas
fornecidas no livro.
I P 7-12
(???l6a)
I
Um bloco de 3.75 kg é puxado com velocidade constante por uma distância de 4.06 m em um piso horizontal por uma corda que exerce uma força de 7.68 N
fazendo um ângulo de 15° acima da horizontal. Calcule
(a) o trabalho executado pela corda sobre o bloco e (b)
o coeficiente de atrito dinâmico entre o bloco e o piso.
21 de Novembro de 2013, às 22:55
onde o valor de N foi obtido da segunda equação acima.
Substituindo o valor de f na primeira das equações
acima e resolvendo-a para J.Lk encontramos sem problemas que
F cos<p
mg - F sen<p
(7.68) cos 15°
(3.57 )(9.8 ) - ()7.68 sen 15
0
7.2.2
= 0.22.
Trabalho executado por força variável
I P 7-16 (???/6 I
a)
A força exercida num objeto é F(x) = Fo(xjxo - 1).
Calcule o trabalho realizado para deslocar o objeto de
x = O até x = 2xo (a) fazendo um gráfico de F(x) e
determinando a área sob a curva e (b) calculando a integral analiticamente.
~ (a) A expressão de F(x) diz-nos que a força varia
linearmente com x. Supondo Xo > O, escolhemos dois
pontos convenientes para, através deles, desenhar uma
linha reta.
Para x = O temos F = - Fo enquanto que para x = 2xo
~ (a) A força na corda é constante, de modo que o tratemos F = Fo, ou seja devemos desenhar uma linha
balho é dado por W = F . d = Fd cos <p, onde F é reta que passe pelos pontos (O, -F ) e (2xo, Fo). Faça
o
a força exercida pela corda, d é a distância do desloca- a figura!
mento, e <p é o ângulo entre a força e o deslocamento. Olhando para a figura vemos que o trabalho total é dado
Portanto
pela soma da área de dois triângulos: um que vai de
x = O até x = Xo, o outro indo de x = Xo até x = 2xo.
W = (7.68)(4.06) cos 15° = 30.1 J.
Como os dois triângulos tem a mesma área, sendo uma
positiva,
a outra negativa, vemos que o trabalho total é
(b) A resposta pode ser obtida facilmente fazendo-se um
ZERO.
diagrama de corpo livre onde constem todas as (quatro)
(b) Analiticamente, a integral nos diz que
forças aplicadas.
Desenhe um ponto P representando o bloco. Em P, desenhe a força normal N apontando para cima, a força
peso mg apontando para baixo. Apontando horizontalmente para a esquerda desenhe a força f de atrito. Desenhe a força F que puxa o bloco apontando para a direita e para cima, fazendo um ângulo <p com a horizontal,
Com isto tudo, a segundo lei de Newton nos diz que para
que o bloco se mova sem acelerar devemos ter equilíbrio
tanto na horizontal quanto na vertical, o que nos fornece
as equações, respectivamente,
f
O,
mg
O.
Fcos<p N
+ F sen <p -
A magnitude da força de atrito é dada por
f
= J.Lk N = J.Lk(mg - F sen<p),
http://www.fisica.ufpb.br/~jgallas
1
2xO
W
=
Fo (:0
Fo (~
2xo
7.2.3
1) dx
-
x)
2XO
1
o
= O.
Trabalho realizado por uma mola
I E 7-18
(7-21/6a)
I
Uma mola com uma constante de mola de 15 N/em está
presa a uma gaiola, como na Fig. 7-31. (a) Qual o trabalho executado pela mola sobre a gaiola se a mola é
distendida de 7.6 mm em relação ao seu estado relaxado? (b) Qual o trabalho adicional executado pela mola
se ela é distendida por mais 7.6 mm?
Página 3 de 7
LISTA 3 - Prof. Jason Gallas, DF-UFPB
~ (a) Quando a gaiola move-se de x =
o trabalho feito pela mola é dado por
w=
l
X2
(-kx)
21 de Novembro
Xl
para
X
=
I E 7-29
Xl
onde k é a constante
Xl = O m e X2 = 7.6
de força da mola. Substituindo
10-3 m encontramos
X
w = -~(1500)(7.6
X
10-3)2
= -0.043
J.
I
(???/6a)
Um carro de 1000 kg está viajando a 60 kmIh numa
estrada plana. Os freios são aplicados por um tempo
suficiente para reduzir a energia cinética do carro de
50 kJ. (a) Qual a velocidade final do carro? (b) Qual
a redução adicional de energia cinética necessária para
fazê-lo parar?
~ (a) A energia cinética inicial do carro é K,
onde m é a massa do carro e
(b) Agora basta substituir-se Xl = 7.6 X 10-3 m e
X2 = 15.2 X 10-3 m na expressão para o trabalho:
Vi
=
60 kmIh
é a sua velocidade
w
- ~ (1500) [(15.2)2 - (7.6)2]
(10-3)2
J.
-0.13
Perceba
alizado
primeiro
idêntico
segundo
X
às 22:55
X2
=
dx
de 2013,
=
60
X
103
=
3600
= mv'f /2,
16.7 m/s
inicial. Isto nos fornece
K, = (1000)(16.7)2/2
= 1.39 x 105 J.
Após reduzir em 50 kJ a energia cinética teremos
que durante o segundo intervalo o trabalho reé mais do que o dobro do trabalho feito no
intervalo. Embora o deslocamento tenha sido
em ambos intervalos, a força é maior durante o
intervalo.
Kf =
1.39
105
X
Com isto, a velocidade
-
50
X
103
=
8.9
X
104 J.
final do carro será
_ J2Kfm _- J2(8.9
x 104)
1000
vf -
13.3 mls
47.8 kmIh.
7.2.4
Energia
I E 7-21
Cinética
(7_???/6G)
(b) Como ao parar a energia cinética final do carro será
ZERO, teremos que ainda remover 8.9 x 104 J para faze10 parar.
I
Se um foguete Saturno V com uma espaçonave ApoIo
acoplada tem uma massa total de 2.9 x 105 kg e atinge
uma velocidade de 11.2 km/s, qual a sua energia cinética
neste instante?
~ Usando a definição de energia cinética temos que
1
= -mv2
K
~(2.9 x 105)(11.2
2
1. 75
I E 7-22
(7-1/6G)
X
x 103)2
1013 J.
I
Um elétron de condução (massa m = 9.11 x 10-31 kg)
do cobre, numa temperatura próxima do zero absoluto,
tem uma energia cinética de 6.7 x 10-19 J. Qual a velocidade do elétron?
~ A energia cinética é dada por K = mv2/2, onde m é
a massa do elétron e v a sua velocidade. Portanto
v=
J2:
=
2(6.7 x 10-19)
6
-9"':".-1-1-x-l""'0--""'31:-'= 1.2 x 10 m/s.
http://www.fisica.ufpb.br/~jgallas
I P 7-35
(7-17l6a)
I
Um helicóptero levanta verticalmente um astronauta de
72 kg até 15 m de altura acima do oceano com o
auxílio de um cabo. A aceleração do astronauta é g/lO.
Qual o trabalho realizado sobre o astronauta (a) pelo
helicóptero e (b) pelo seu próprio peso? Quais são (c)
a energia cinética e (d) a velocidade do astronauta no
momento em que chega ao helicóptero?
~ (a) Chame de F a magnitude da força exercida pelo
cabo no astronauta. A força do cabo aponta para cima e
o peso mg do astronauta aponta para baixo. Além disto,
a aceleração do astronauta é 9 /10, para cima. De acordo
com a segunda lei de Newton,
F - mg
= mg/10,
de modo que F = 11mg/lO. Como a força F e o deslocamento d estão na mesma direção, o trabalho feito pela
força F é
WF=Fd=
11mg d
10
11(72) (9.8) (15)
10
Página 4 de 7
LISTA 3 - Prof. Jason Gallas, DF-UFPB
21 de Novembro de 2013, às 22:55
7.2.5 Potência
1.16
X
104 J.
(b) O peso tem magnitude mg e aponta na direção
oposta do deslocamento. Ele executa um trabalho
Wg
=
= -(72)(9.8)(15)
-mgd
= -1.06
x 10 J.
(c) O trabalho total feito é
WT = 11600 - 10600 = 1000 J.
Como o astronauta partiu do repouso, o teorema do
Trabalho-Energia diz-nos que sua energia cinética final
deverá ser igual a WT
(d) Como K = mv2/2, a velocidade final do astronauta
será
v= J2: =
I P 7-36
2(1000) = 5.27 mls = 18.9 kmJh.
72
(7-19/6a)
I
Uma corda é usada para fazer descer verticalmente um
bloco, inicialmente em repouso, de massa M com uma
aceleração constante 9 / 4. Depois que o bloco desceu
uma distância d, calcule (a) o trabalho realizado pela
corda sobre o bloco, (b) o trabalho realizado sobre o
bloco pelo seu peso, (c) a energia cinética do bloco e (d)
a velocidade do bloco.
~ (a) Chame de F a magnitude da força da corda sobre o bloco. A força F aponta para cima, enquanto que
a força da gravidade, de magnitude M g, aponta para
baixo. A aceleração é 9 / 4, para baixo. Considere o
sentido para baixo como sendo o sentido positivo. A segunda lei de Newton diz-nos que M 9 - F = M 9 / 4,
de modo que F = 3M 9/ 4. A força está direcionada no
sentido oposto ao deslocamento de modo que o trabalho
que ela faz é
WF
(???/6a)
I
Um bloco de granito de 1400 kg é puxado por um guindaste a vapor ao longo de uma rampa com velocidade
constante de 1.34m1s (Fig. 7-38). O coeficiente de atrito
dinâmico entre o bloco e a rampa é 0.4. Qual a potência
do guindaste?
~ Para determinar a magnitude F da força com que
o guindaste puxa o granito usaremos um diagrama de
corpo livre.
Chamemos de f a força de atrito, no sentido oposto ao
de F. A normal N aponta perpendicularmente à rampa,
enquanto que a magnitude mg da força da gravidade
aponta verticalmente para baixo.
Da figura dada vemos que ângulo B do plano inclinado
vale
Tomemos o eixo x na direção do plano inclinado, apontando para cima e o eixo y apontando no mesmo sentido
da normal N.
Como a aceleração é zero, as componentes x e y da segunda lei de Newton são, respectivamente,
F-
f - mg senB
N-mgcosB
O,
O.
Da segunda equação obtemos que N = mg cos B, de
modo que f = J.lkN = J.lkmgcosB. Substiutindo este
resultado na primeira equação e resolvendo-a para F
obtemos
3
= -Fd = -"'4Mgd.
(b) A força da gravidade aponta no mesmo sentido
que o deslocamento de modo que ela faz um trabalho
Wg = Mgd.
(c) O trabalho total feito sobre o bloco é
3
WT
I P 7-43
4
A força do guindaste aponta no mesmo sentido que a velocidade do bloco, de modo que a potência do guindaste
é
1
= -"'4Mgd+ Mgd = "'4 Mgd.
Como o bloco parte do repouso, o valor acima coincide
com sua energia cinética K após haver baixado uma
distância d.
(d) A velocidade após haver baixado uma distância d é
v=J~ =fif·
http://www.fisica.ufpb.br/~jgallas
P
Fv
mgv (sen B + J.lkcos B)
(1400)(9.8)(1.34) (sen 37°
+ 0.4 cos 37°)
17kW.
Página 5 de 7
LISTA 3 - Prof. Jason Gallas, DF-UFPB
I P 7-47
(???/6a)
21 de Novembro de 2013, às 22:55
I
Uma força de 5 N age sobre um corpo de r.5 kg inicialmente em repouso. Determine (a) o trabalho executado
pela força no primeiro, segundo e terceiro segundos e
(b) a potência instantânea aplicada pela força no final
do terceiro segundo.
~ (a) A potência é dada por P = Fv e o trabalho feito
por F entre o instante ti e t2 é
W
=
t2
l
P dt
t,
=
lt2
Fv dto
t,
Como F é a força total, a magnitude da aceleração é
a = f /m e a velocidade em função do tempo é dada
por v = at = Ftf m: Portanto
W =
t2 F2t dt
l
-
rri
t,
1F2
= - - (t~ 2 m
o sistema: WT = We + Wc + Wrn. Como o elevador
move-se com velocidade constante, sua energia cinética
não muda e, de acordo com o teorema do TrabalhoEnergia, o trabalho total feito é zero. Isto significa que
We + Wc + Wrn = O.
O elevador move-se 54 m para cima, de modo que o trabalho feito pela gravidade sobre ele é
We
=
-megd
-(1200)(9.8)(54)
=
=
-6.35 x 105 J.
O contrapeso move-se para baixo pela mesma distância,
de modo que o trabalho feito pela gravidade sobre ele é
Wc
=
mcgd
Como WT
=
(950)(9.8)(54)
=
=
5.03 x 105 J.
O,o trabalho feito pelo motor é
(6.35 - 5.03) x 105
ti) .
1.32
X
105 J.
Para ti = Ose t2 = ls temos
Wi
=
21 (52)
15 [2
(1) - (O)2] = 0.83 J.
Este trabalho é feito num intervalo de tempo 6..t
3 min = 180 s e, portanto, a potência fomecida pelo
motor para levantar o elevador é
Para t: = ls e t2 = 2s temos
W2
Para ir
= 21 (52)
15 [(2) 2 - (1) 2] = 2.5 J.
=
Wrn
6..t
= (5)2(3) = 5 W.
P
15
(7-35/6a)
I
Um elevador de carga totalmente cheio tem uma massa
total de 1200 kg e deve subir 54 m em 3 mino O contrapeso do elevador tem uma massa de 950 kg. Calcule a potência (em cavalos-vapor) que o motor do elevador deve desenvolver. Ignore o trabalho necessário
para colocar o elevador em movimento e para freá-lo,
isto é, suponha que se mova o tempo todo com velocidade constante.
~ O trabalho total é a soma dos trabalhos feitos pela
gravidade sobre o elevador, o trabalho feito pela gravidade no contrapeso, e o trabalho feito pelo motor sobre
http://www.fisica.ufpb.br/~jgallas
=
5
1.32 X 10
180
=
735 W.
Este valor corresponde a
= 2s e t2 = 3s temos
(b) Substitua v = Fif m. em P = Fv obtendo então
P = F2t/m para a potência num instante t qualquer.
Ao final do terceiro segundo temos
I P 7-48
P
735 W =
h
746 Wlhp
0.99 p.
I P 7-49
(???/6a)
I
A força (mas não a potência) necessária para rebocar um
barco com velocidade constante é proporcional à velocidade. Se são necessários 10 hp para manter uma velocidade de 4 kmIh, quantos cavalos-vapor são necessários
para manter uma velocidade de 12 km/h?
~ Como o problema afirma que a força é proporcional
à velocidade, podemos escrever que a força é dada por
F = av, onde v é a velocidade e a é uma constante de
proporcionalidade. A potência necessária é
P
= Fv = av2•
Esta fórmula nos diz que a potência associada a uma
velocidade Vi é Pi = aVf e a uma velocidade V2 é
P2 = av~. Portanto, dividindo-se P2 por Pi podemos
nos livrar da constante a desconhecida, obtendo que
Página 6 de 7
LISTA 3 - Prof. Jason Gallas, DF-UFPB
21 de Novembro de 2013, às 22:55
Para P1 = 10 hp e V2 = 3Vl, vemos sem problemas que
P2
12)2
= ( "4
(10)
-
= (3)2(10) = 90 hp.
Observe que é possível determinar-se explicitamente o
valor de a a partir dos dados do problema. Porém, tal
solução é menos elegante que a acima apresentada, onde
determinamos a implicitamente, chegando ao resultado
final mais rapidamente.
(b) Como a velocidade do elétron é próxima da velocidade da luz,devemos usar expressão relativística para a
energi a cinética:
K
( VI - ~0.68)2 3.0
7.2.6
X 10-14
1)
J.
Energia Cinética a Velocidades Elevadas
Este valor é equivalente a
I E 7-50
(???/6a)
I
K
3.0
= 1.60
X
X
10-14
10-19
= 1.90
X
5
10
= 190 keV.
Um elétron se desloca de 5.1 em em 0.25 ns. (a) Qual é
a relação entre a velocidade do elétron e a velocidade da
luz? (b) Qual é a energia do elétron em elétrons-volt?
(c) Qual o erro percentual que você cometeria se usasse
a fórmula clássica para calcular a energia cinética do
elétron?
(c) Classicamente a energia cinética é dada por
~ (a) A velocidade do elétron é
Portanto, o erro percentual é, simplificando já a potência
comum 10-14 que aparece no numerador e denominador,
d
V
= - =
t
5.1 X 10-2
0.25 X 10-9
= 2.04
Como a velocidade da luz é c = 2.998
v
2.04
c
2.998
= --
X
108 m/s.
X 108
1
2
K = -mv2
~(9.1l x 10-31)(2.04 x 108?
1.90 x 10-14 J.
erro percentual =
m/s, temos
= 0.68 c.
http://www.fisica.ufpb.br/~jgallas
3.0 - 1.9
3.0
= 0.37,
ou seja, 37%. Perceba que não usar a fórmula relativística produz um grande erro!!
Página 7 de 7