SEMI Prova

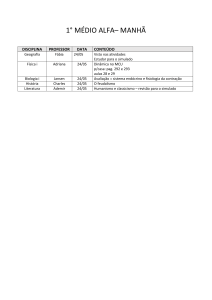
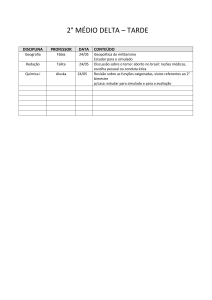
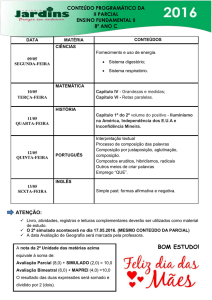
SEMI
16 de maio de 2014
Simulado
1. Assinale a soma dos itens associados as proposições verdadeiras:
01. A quantidade de números naturais que podem ser decompostos em um produto de quatro fatores primos, positivos e distintos, considerando que os quatro sejam menores que 30, é 210.
02. Vinte times de futebol disputam a Série A do Campeonato
Brasileiro, sendo três deles Catarinenses (Figueirense, Chapecoense e Criciúma). Cada time joga duas vezes contra cada
um dos seus adversários. A porcentagem de jogos nos quais
os dois oponentes são catarinenses está entre 1 e 2 por cento.
04.Dez mulheres e seis homens participarão de um torneio de xadrez. Sabendo que essas 16 pessoas devem necessariamente
ser separadas nos grupos X, Y, W e Z, cada um deles com 4 jogadores e que os grupos X e W serão formados apenas por mulheres e o grupo Y, apenas por homens. O número de maneiras
distintas que podemos formar esses grupos é 42750.
08.Se uma partida de Polo Aquático termina com o resultado de
6 gols para o time Aquaman e 2 gols para o time Poseidon existem diversas maneiras de o placar evoluir, o número de maneiras para este placar evoluir possui 12 divisores.
2
Simulado
2. Assinale a soma dos itens associados as proposições verdadeiras:
01. Na sequência de quadros a seguir, o valor da primeira célula
de cada quadro é a soma dos valores das duas últimas células
do quadro anterior.
Se o número da célula central do último quadro dessa sequência é 2²⁰¹⁴, então o produto dos números das outras células
será 2⁴⁰²⁶ − 1.
02. O par ordenado (x, y) ! N × N é solução da equação x³ + x²y – 8x – 8y = 7. O valor de x + y é um número primo.
04.É possível fatorar o polinômio P(x) = x⁵ + x² – x – 1 em um produto
de dois polinômios, sendo um deles de grau 3.
08.Simplificando a expressão
3
2
3
x na qual x ! R * obtém-se 12 x .
+
x4
16. Se x é um número real positivo e menor do que 1, x > x .
R
V R
V
32. Se k = SS 2 – c 1 mWW · SS 2 + c 1 mWW e m = 2 +
3
3
T
X T
X
(k − 1)³ + (m − 2)³ é igual a 62/27.
3
16 de maio de 2014
2
, então 2
3
3. Assinale a soma dos itens associados as proposições verdadeiras:
01. A soma dos elementos da diagonal principal com os elementos da diagonal secundária da matriz transposta da matriz
a ij = i 2 + 1 se i = j
A 2 # 2 = ' a = 2i + j se i ≠ j , é um número primo.
ij
02. Dada a equação matricial c
x 2
0 1
4 8
m·c
m=c
m o valor do proy z
1 3
2 3
duto xyz é 120.
04. Sejam as matrízes A = c
1 2
–1 3
. O valor de x para o
m e B=`
3 4
x 2j
qual o determinante de A · B se anula é − 2/3
4
Simulado
08.Após assistir a uma aula sobre determinantes de matrizes, Pedro decidiu codificar sua senha bancária. A senha é composta
pelos números A, B, C e D, justapostos nessa ordem e codificados através dos determinantes abaixo:
R1 2 4V
S
W
A = S3 1 2W
S1 2 1W
T
X
1
2
C=
4
8
2
4
8
16
0
–3
–2
0
–2
–3
–1
–2
7
3
0
0
–1
–8
2
0
25
32
11
1
–3
0
D= 0
0
0
0
–2
0
0
0
0
0
4
0
0
1
0
B=
0
0
0
0
0
1
0
0
0
0
0
1
Então, temos que a senha de Pedro possui 6 dígitos.
–1 0 –1
16. A lei de formação da matriz A = 8
é 7 1 1B
2i – j, se i < j
A = 6a ij@2 # 3 = * (– 1) i, se i = j
– i 2 + 3j, se i > j
16 de maio de 2014
5
4. Assinale a soma dos itens associados as proposições verdadeiras:
01. Dentro de um grupo de tradutores de livros, todos os que falam português também falam inglês, mas nenhum que fala
inglês fala japonês. Além disso, os dois únicos que falam latim
também falam coreano. Sabendo que todo integrante desse
grupo que fala coreano também fala japonês, pode-se concluir que, pelo menos um tradutor que fala inglês também fala
coreano.
02. Considere dois conjuntos finitos A e B tais que: A 1 B, A + B ≠ Q
e A , B ≠ A. Nestas condições pode-se afirmar que o conjunto B
possui a mesma quantidade de elementos que o conjunto A.
04.Dois pontos A e B estão situados na margem de um rio e distantes 40 m um do outro. Um ponto C, na outra margem do rio,
está situado de tal modo que o ângulo CÂB mede 75° e o ângulo
AĈB mede 75°. Então a largura do rio é 20 metros.
08.Um triângulo T tem lados iguais a 4, 5 e 6. O cosseno do maior
ângulo de T é 1/8.
6
Simulado
5. Assinale a soma dos itens associados as proposições verdadeiras:
01. Suponha que o litro da gasolina aumentou 10%. Se um proprietário de carro o abastecia com 55 litros de gasolina, após o aumento, com a mesma quantia de dinheiro, ele abastecerá 60,5
litros.
02. Se Pedro pesa 120 kg e senta a 1 m do centro de apoio de uma
gangorra, então Sidi, que pesa 75 kg, deverá sentar a 1,6 m do
centro para que a gangorra fique em equilíbrio.
04.Se log 2 = 0,3 e log 3 = 0,48, então, um automóvel cujo valor de mercado hoje é de R$ 30.000,00 e cuja desvalorização é de 4% ao ano
de juros compostos, então, em 20 anos, ele valerá R$ 15.000,00.
08. Se a soma de quatro números primos distintos é igual a 145,
então o menor deles é 2.
16. Erivaldo e Marli pretendem viajar e foram a uma casa de câmbio, onde receberam as seguintes informações: com os 3.060
reais de que dispunha, Erivaldo poderia comprar 1.500 dólares
e, com os 3.250 reais de Marli, seria possível comprar 1.250 euros.
Com base nessas informações, é correto afirmar que, nesse dia,
a cotação do euro em relação ao dólar era de 1,2745.
16 de maio de 2014
7
nome
semi
extensivo
grupo
top100
intensivo
1
2
3
4
5