3B – MRU, encontro de MRU e MRUV, corpo extenso

3B – MRU, encontro de MRU e MRUV, corpo extenso
Nome
Nº
1ª série
Física – Beth/Reinaldo
Data
/
/2016
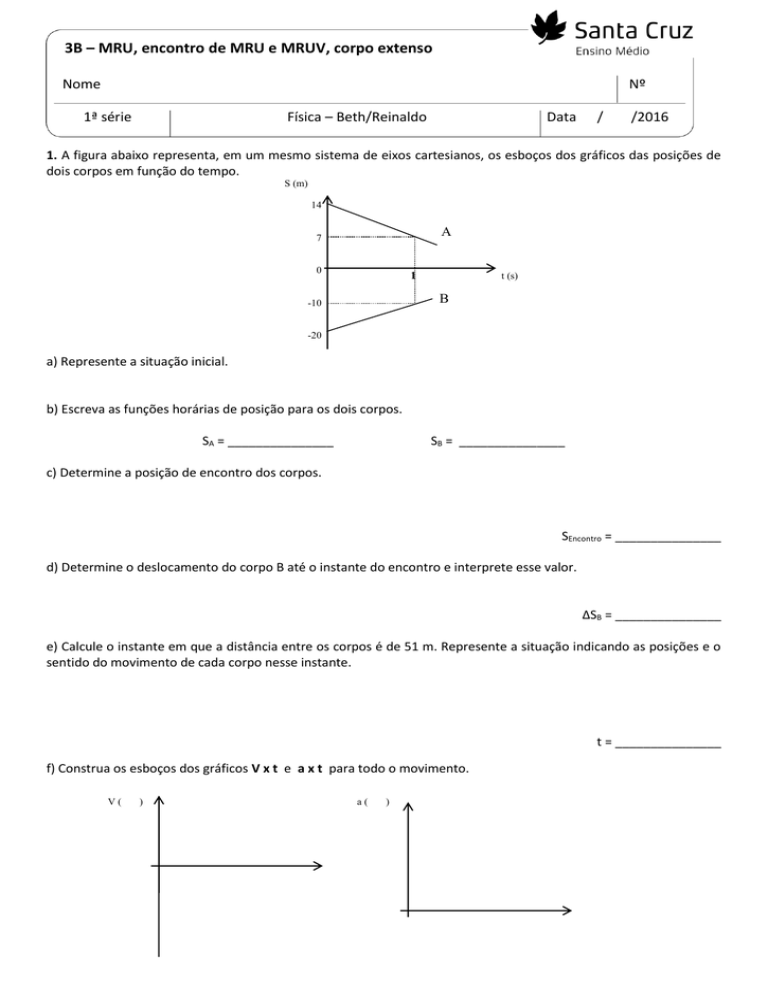
1. A figura abaixo representa, em um mesmo sistema de eixos cartesianos, os esboços dos gráficos das posições de
dois corpos em função do tempo.
S (m)
14
A
7
0
1
t (s)
B
-10
-20
a) Represente a situação inicial.
b) Escreva as funções horárias de posição para os dois corpos.
SA = _______________
SB = _______________
c) Determine a posição de encontro dos corpos.
SEncontro = _______________
d) Determine o deslocamento do corpo B até o instante do encontro e interprete esse valor.
∆SB = _______________
e) Calcule o instante em que a distância entre os corpos é de 51 m. Represente a situação indicando as posições e o
sentido do movimento de cada corpo nesse instante.
t = _______________
f) Construa os esboços dos gráficos V x t e a x t para todo o movimento.
V(
)
a(
)
2. (Unesp 2014-adapt.) Um motorista dirigia por uma estrada
plana e retilínea quando, por causa de obras, foi obrigado a
desacelerar seu veículo, reduzindo sua velocidade de
90 km/h para 54 km/h. Depois de passado o trecho em obras,
retornou à velocidade inicial de 90 km/h. O gráfico representa
como variou a velocidade escalar do veículo em função do
tempo, enquanto ele passou por esse trecho da rodovia.
Considere que em t0 = 0 ele se encontra no quilometro 0.
a) Para cada intervalo abaixo, escreva se a pessoa foi para frente ou para trás, acelerando, freando ou com
velocidade constante.
0 a 10 s
10 s a 20 s
20 s a 40 s
40 s a 60 s
60 s a 80 s
b) Represente a trajetória do corpo durante todo o movimento, indicando S0 e as posições finais de cada trecho.
c) Qual foi a velocidade média do carro entre 0 e 80 s? Resp.: ___________
a(
)
d) Esboce no eixo ao lado o gráfico axt para os primeiros
40 s do movimento.
e) Caso não tivesse reduzido a velocidade devido às obras, mas mantido sua velocidade constante de 90 km/h
durante os 80 s representados no gráfico, calcule a distância adicional que teria percorrido nessa estrada.
Resp.: ___________
2
3. Amaro e Betina estão numa pista retilínea. Amaro, que está parado na origem da pista, parte em direção a Betina,
com aceleração constante de 2 m/s2. No mesmo instante, Betina passa pela posição 20m da pista, movendo-se com
velocidade constante de - 1 m/s, em direção a Amaro. Responda as questões abaixo.
a) Faça um desenho representando a situação inicial.
b) Escreva as funções horárias da posição, velocidade e aceleração para o movimento de Amaro (A) e Betina (B);
SA = _______________
SB = _______________
VA = _______________
VB = _______________
aA = _______________
aB = _______________
c) Após quanto tempo eles se encontram?
h) Esboce os gráficos Sxt, Vxt e axt do movimento de
Amaro e Betina, colocando-os juntos em cada um dos
três gráficos. Use os eixos fornecidos e indique o ponto
de encontro nos gráficos Sxt e Vxt.
t = ____________
d) Qual é a posição de encontro?
S(
)
S = ____________
e) Indique no desenho acima a posição de encontro e
justifique por que está mais próxima de um deles do
que do outro.
f) Calcule a velocidade de Amaro na posição de encontro.
V(
)
a(
)
V = _________________
g) Calcule a velocidade média de Amaro até a posição de
encontro.
VM = _________________
3
4. Um trem de 100 m de comprimento se desloca com velocidade de 72 km/h. Esse trem, ao iniciar a travessia de uma
ponte, acelera uniformemente, saindo completamente da mesma após 12 s. O comprimento da ponte é o dobro do
comprimento do trem. Represente a situação inicial e calcule a velocidade do trem no instante em que ele atravessa
completamente a ponte.
4