1. (UFSCar SP/2000/1ª Fase) Um polígono regular com exatamente

1. (UFSCar SP/2000/1ª Fase)
Um polígono regular com exatamente 35 diagonais tem
a) 6 lados.
b) 9 lados.
c) 10 lados.
d) 12 lados.
e) 20 lados.
Gab: C
2. (Unifor CE/1999/Janeiro)
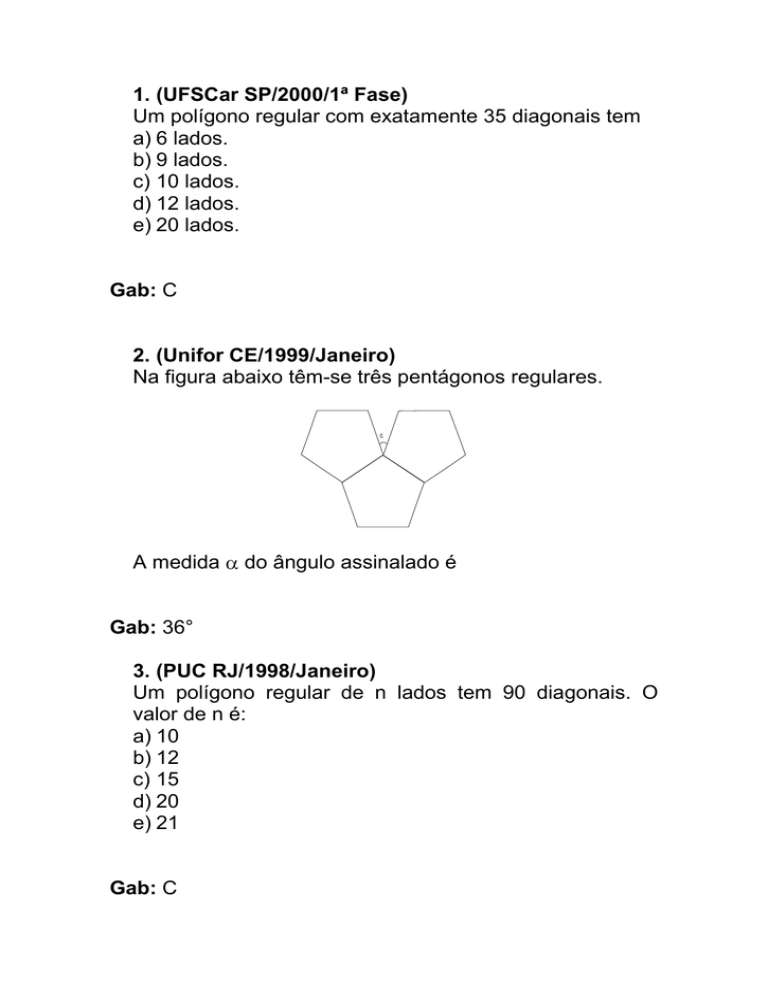
Na figura abaixo têm-se três pentágonos regulares.
A medida
do ângulo assinalado é
Gab: 36°
3. (PUC RJ/1998/Janeiro)
Um polígono regular de n lados tem 90 diagonais. O
valor de n é:
a) 10
b) 12
c) 15
d) 20
e) 21
Gab: C
4. (Fuvest SP/1997/1ª Fase)
A, B, C e D são vértices consecutivos de um hexágono
regular. A medida, em graus, de um dos ângulos
formados pelas diagonais AC e BD é
a) 90
b) 100
c) 110
d) 120
e) 150
Gab: D
5. (UEPB PB/2007)
Aumentando-se de 5 unidades o número de lados de um
polígono, o número de diagonais aumenta de 40. Esse
polígono é o:
a) heptágono
b) pentágono
c) hexágono
d) octógono
e) eneágono
Gab: A
6. (Unifor CE/2007/Janeiro)
Os lados de um octógono regular são prolongados até
que se obtenha uma estrela. A soma das medidas dos
ângulos internos dos vértices dessa estrela é
a) 180.
b) 360.
c) 540.
d) 720.
e) 900.
Gab: D
7. (Unificado RJ/1994)
ABCDE é um pentágono regular convexo. O ângulo das
diagonais AC e AD vale:
a) 30°
b) 36°
c) 45°
d) 60°
e) 72°
Gab: B
8. Num polígono, o número de diagonais é o dobro do
número de lados. A soma de seus ângulos internos é
em graus:
a) 900
b) 1080
c) 1260
d) 1440
9. Se a medida de um ângulo interno de um polígono
regular é 150°, a soma dos ângulos internos deste é:
a) 1240°
b) 2240°
c) 3240°
d) 1800°
10.
A soma dos ângulos internos de um polígono
convexo é 2340º. Calcular a quantidade de diagonais
desse polígono.