Document

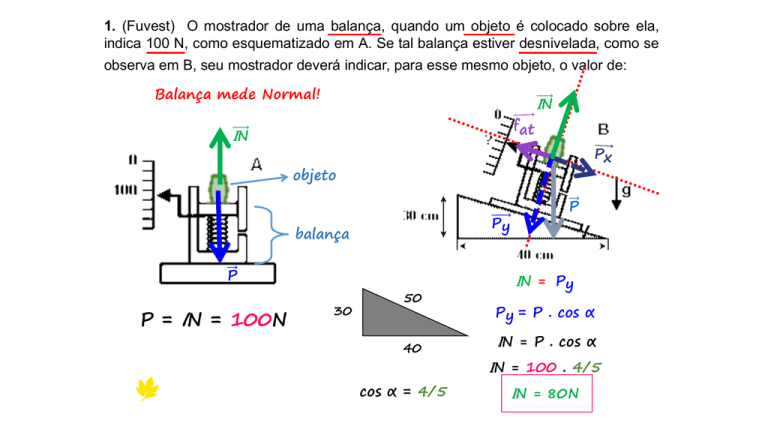
1. (Fuvest) O mostrador de uma balança, quando um objeto é colocado sobre ela,
indica 100 N, como esquematizado em A. Se tal balança estiver desnivelada, como se
observa em B, seu mostrador deverá indicar, para esse mesmo objeto, o valor de:
Balança mede Normal!
IN
IN
objeto
Py
balança
P
P = IN = 100N
30
50
40
cos α = 4/5
P
I N = Py
Py = P . cos α
IN = P . cos α
IN = 100 . 4/5
IN = 80N
2. (Fgv-adapt.) Dois carrinhos de supermercado podem ser acoplados um ao outro por meio de uma pequena corrente, de
modo que uma única pessoa, ao invés de empurrar dois carrinhos separadamente, possa puxar o conjunto pelo interior do
supermercado. Um cliente aplica uma força horizontal de intensidade F, sobre o carrinho da frente, dando ao conjunto uma
aceleração de intensidade 0,25 m/s2.
Sendo o piso plano e as forças de atrito desprezíveis, calcule o módulo da força F e o da força de tração T na corrente, em
newton.
IN
IN
R = m . a
1: F - T = m1 . a
2: T = m2 . a
T21
F = (m1 + m2). a
T12
F = 140 . 0,25
F = 35 N
P (400N)
P (1000N)
2: T = m2 . a
MRUV
T = 100 . 0,25
T = 25 N
3. (Ufmg-adapt.) Nessa figura, está representado um bloco de 3,0kg sendo pressionado contra a parede por uma força F.
Os coeficientes de atrito entre o bloco e a parede são 0,5, e 0,3.
a) Represente todas as forças que atuam no bloco.
b) Calcule a força mínima F que deve ser aplicada ao bloco para que ele não deslize na parede.
Equilíbrio (repouso): a = 0 → R = 0
IN
fat
em
P = fat
em
F = IN
fat
= μe . IN
em
P (30N)
fat
= 0,5 . F
em
30 = 0,5 . F
F = 60 N
4. (Uel) Um corpo de peso 10 N é puxado plano acima, com velocidade
constante, por uma força F paralela ao plano inclinado de 53° com a
horizontal. Adote: cos53° = 0,60; sen53° = 0,80; g = 10m/s2;
µ = 0,20 e µ = 0,30. A intensidade da força F é, em newtons,
P = 10N
IN
Velocidade constante → R = 0
IN = Py
Py
P
F = Px + fat
c
Px = P . sen 53 = 10 . 0,80 = 8N
Py = P . cos 53 = 10 . 0,60 = 6N
IN = Py = 6N
fat = μc . IN
c
fat = 0,2 . 6
c
fat = 1,2 N
c
F = Px + fat
c
F = 8 + 1,2
F = 9,2 N
5. Um caixote em equilíbrio, de massa de 100 kg, é puxada sobre um
piso horizontal por uma força F = 600 N que forma um ângulo de 30°
com a horizontal, conforme representado na figura.
a) Represente e nomeie todas as forças atuantes no caixote nas
direções perpendicular e paralela ao plano.
b) Determine o módulo das forças Peso, Normal e de atrito que
atuam sobre o caixote?
P = 1000 N
F = 600 N
Equilíbrio: a = 0 → R = 0
Fy
IN
F
IN + Fy = P
30°
Fx = fat
Fx
P
Fy
IN
F
P = 1000 N
F = 600 N
30°
Fx
R = 0
P
Fy
F
IN + Fy = P
30º
IN + 300 = 1000
Fx
IN = 700 N
Fy = F . sen 30
Fx = F . cos 30
Fy = 600 . 0,5
3
Fx = 600 . 2
Fy = 300 N
Fx = 510 N
fat = Fx
fat = 510 N