Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
HALLIDAY, RESNICK, WALKER, FUNDAMENTOS DE FÍSICA, 4.ED., LTC, RIO DE
JANEIRO, 1996.
FÍSICA 2
CAPÍTULO 8 – CONSERVAÇÃO DA ENERGIA
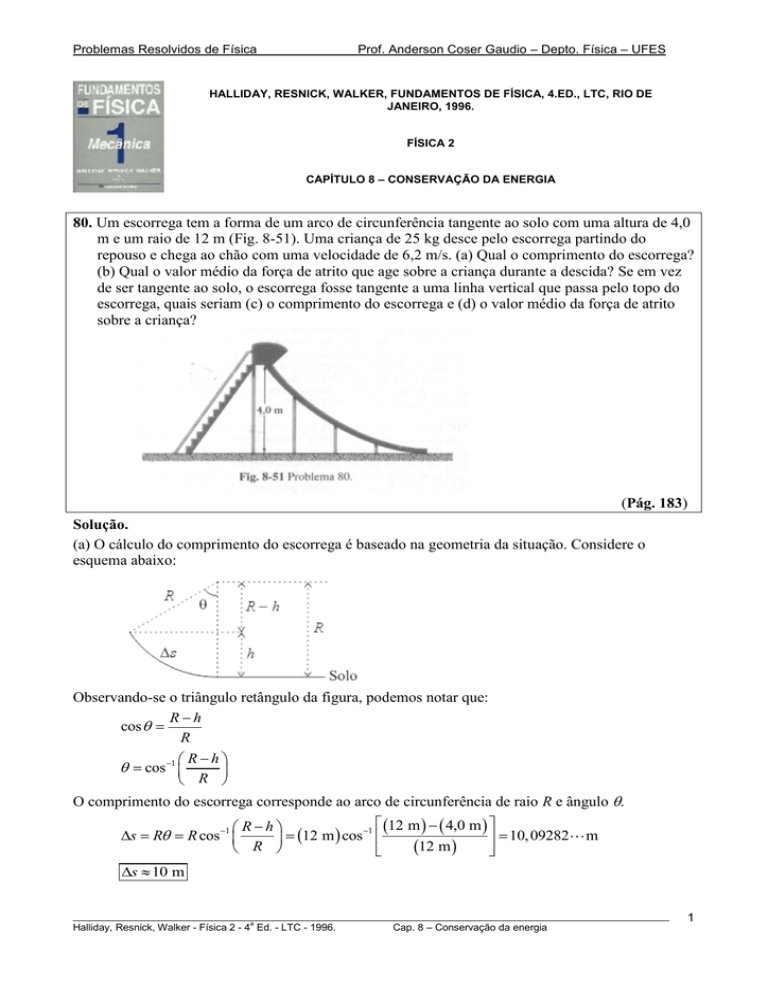
80. Um escorrega tem a forma de um arco de circunferência tangente ao solo com uma altura de 4,0
m e um raio de 12 m (Fig. 8-51). Uma criança de 25 kg desce pelo escorrega partindo do
repouso e chega ao chão com uma velocidade de 6,2 m/s. (a) Qual o comprimento do escorrega?
(b) Qual o valor médio da força de atrito que age sobre a criança durante a descida? Se em vez
de ser tangente ao solo, o escorrega fosse tangente a uma linha vertical que passa pelo topo do
escorrega, quais seriam (c) o comprimento do escorrega e (d) o valor médio da força de atrito
sobre a criança?
(Pág. 183)
Solução.
(a) O cálculo do comprimento do escorrega é baseado na geometria da situação. Considere o
esquema abaixo:
Observando-se o triângulo retângulo da figura, podemos notar que:
Rh
cos  
R
 Rh
  cos 1 

 R 
O comprimento do escorrega corresponde ao arco de circunferência de raio R e ângulo .


 Rh
1 12 m    4,0 m 
s  R  R cos1 
  10, 09282
  12 m  cos 
12
m


 R 


m
s  10 m
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação da energia
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
(b) Se não houvesse dissipação de energia durante a descida, a velocidade final da criança seria
v  2 gh  8,9 m/s . Como foi dito que a velocidade final é de apenas 6,2 m/s, deduz-se que a força
relativa ao atrito entre a criança e o escorrega executa trabalho no sentido de roubar energia
mecânica do sistema. Ou seja:
E  Wat   Fat  ds
Note que a força de atrito é variável. Esta depende da força normal, que por sua vez é variável ao
longo da rampa. Podemos eliminar essa complicação tomando-se a força de atrito média ( Fat ) para
efetuar o cálculo do trabalho, o que elimina a necessidade de cálculo integral.
E   Fat  ds   Fat ds cos 180    Fat  ds   Fat s
Escrevendo a energia mecânica em termos de energia potencial e cinética, teremos:
E  U  K   Fat s
U  U0    K  K0    Fat s
No início do movimento, a velocidade da criança é nulo, logo K0 = 0. Ao final do movimento, no
solo, sua energia potencial é nula, ou seja, U = 0.
 0  U0    K  0  Fat s
K U0 
1 2
mv  mgh   Fat s
2
 6, 2 m/s   2  9,81 m/s2   4, 0 m 
v 2  2 gh
Fat  m
   25 kg 
 49,5897
2s
2 10, 09282 m 
2
N
Fat  50 N
(c) Considere o seguinte esquema da nova situação:
De acordo com a figura acima, nota-se que:
h
sen  ' 
R
h
 '  sen 1  
R
Mas:
  4,0 m  
h
s '  R '  R cos 1    12 m  cos 1 
  4, 07804
12
m


R


m
s '  4,1 m
(d) Neste caso, a força de atrito média terá o valor de:
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação da energia
2
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
 6, 2 m/s   2  9,81 m/s2   4, 0 m 
v 2  2 gh
F  m
   25 kg 
 122, 7305
2s '
2  4, 07804 m 
2
'
at
N
Fat'  0,12 kN
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 8 – Conservação da energia
3