09296515-Folhas Verdes-Site_Resolução_Física

Física II – Resolução
Capítulo 19
Capítulo 18
Trabalho e Energia
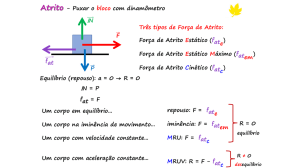
Força de Atrito
1.
1.
D
Só haverá movimento se a resultante de todas as forças tiver
intensidade maior que a da força de atrito estática máxima.
2.
D
Observem:
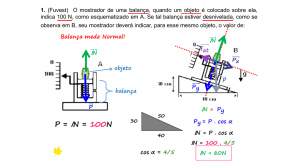
B
Dados: m1 = 6 kg; m2 = 1,5 kg; g = 10 m/s2; ∆S = 30 m;
α = 60°.
Para o corpo de massa m2 subir com velocidade constante,
então:
F = P2 = m2g = 15 N.
T
O trabalho realizado (W) para arrastar a mochila é:
W = F ∆S cos 60° = (15) (30) (0,5) ⇒ W = 225 J.
NB
N
A
FatA
2.
T
D
B
A
PvA
60º
PxA
F
N
FatB
P · sen 30º
P · cos 30º
P
Como os dois estão em repouso, temos:

A →



B →

Velocidade constante (a = 0) e despreze as perdas por atrito.
1
F – P · sen 30º = 0 → F = 1 200 · 10 · = 6 000 N
2
60
36 . 104
Pot = F · v = 6 000 ·
=
= 105 W = 102 . 103 W
3, 6 36 . 10−1
Pot = 100 · 103 W = 100 kW
T + FatA = Px A
NA = Py A
T = FatB
⇒ Fat = Px – Fat ⇒ Fat =
B
A
A
B
NB = PB
PA sen 60º – µ NA ⇒ Fat = PA sen 60º – µ PA cos 60º ⇒
B
Fat = 1 000 × 0,87 – 0,1 × 1000 × 0,5 = 870 – 50 ⇒ Fat = 820 N
B
3.
3.
B
C
Utilizando o teorema do trabalho-energia, temos:
WP + WN + Wa + We = EC – EC0
D
Dados: g = 10 m/s2; µe = 0,60; µc = 0,80; m = 1200 kg.
1 2
1
kx = 0 − mV02
2
2
1
1
– µx40 × 0,7 – × 200 × (0,1)2 = – 4(2)2
2
2
7
28µ = 8 – 1 = 7 ⇒ µ =
= 0,25
28
0 + 0 − µNd −
Temos:
N = P = mg = 12.000 N.
A força de atrito estático máxima: Fat máx = µeN = 0,8 (12.000)
⇒ Fat Max = 9.600 N.
A força de atrito cinético: Fat cin = µcN = 0,6 (12.000)
⇒ Fat cin = 7.200 N.
4.
30º
4.
B
Dados: m = 900 kg; F = 2 900 N; µc = 0,25; µE = 0,35;
g = 10 m/s2.
E
A definição da energia cinética é:
EC =
mv 2
2
Em relação:
Força de atrito estático máxima:
• ao carro, a velocidade da criança é nula.
Fat máx = µE · N = µE · mg = 0,35 · 900 · 10 = Fat máx = 3 · 150 N.
EC = 0
• à estrada, a velocidade da criança é de 72 km/h = 20 m/s.
40 . 202
EC =
= 8 000 J
2
A força de atrito estático máxima tem maior intensidade
que aplicada paralelamente ao plano, o bloco não entra em
movimento. Assim, a força resultante sobre ele é nula.
Então:
Fat = F ⇒ Fat = 2900 N
ensino médio
1
1º ano
Capítulo 20
Trabalho e Energia
1.
B
Dados: m = 70 kg; v0 = 10 m/s; ∆EC = 0,7 (500) = 350 J.
A energia cinética depois do salto é igual à energia cinética
inicial somada à variação adquirida no salto.
mv 2 mv 20
ECf = EiC + ∆EC ⇒
=
+ ∆EC ⇒
2
2
70 v 2 70 (10)
=
+ 350 ⇒
2
2
35 v 2 = 35 (100) + 350 ⇒
2
⇒
v 2 = 100 + 10 ⇒ v = 110 ⇒
v = 10,5 m/s.
2.
B
Cálculo do trabalho das forças dissipativas entre entre 0 4s:
Wfdiss = E(final) – E(inicial) = 600 – 1800 = – 1 200 J
Em módulo: 1.200J
3.
C
Dados do gráfico: x0 = 0; t = 2s ⇒ (v = 0 e x = 20 m).
Movimento uniformemente variado (MUV).
Então:
v = v 0 + at ⇒ 0 = v 0 + a (2) ⇒ v 0 = − 2 a (I)

t=2s ⇒
a 2
a 2
x = v 0t + t ⇒ 20 = v 0 (2) + (2) ⇒ 20 = 2v 0 + 2a
2
2

(II)
I em II:
20 = 2(– 2a) + 2a ⇒ 2a = – 20 ⇒ | a | = 10 m/s2
Em I:
v0 = – 2a ⇒ v0 = – 2(– 10) ⇒ | v0 | = 20 m/s
4.
D
EmA = mgh = 25.10.2,4 = 600 J
EmB = mV2/2 = 25V2/2 = 12,5V2
Fat = µN = mP cos 37 = 0,5.250.0,8 = 100 N
sen37º = h/d
d=4m
Wfat = Fat · d · cos 37º = 100 · 4 · 0 · (–1) = – 400J
Wfat = EmB – EmA
– 400 = 12,5V2 – 600
V = 4 m/s
ensino médio
2
1º ano