MUV_1 - Professor Ubiratan

MOVIMENTO UNIFORMEMENTE VARIADO
1.
O cérebro humano demora cerca de 0,36 segundos para responder a um
estímulo. Por exemplo, se um motorista decide parar o carro, levará no mínimo
esse tempo de resposta para acionar o freio.
Determine a distância que um carro a 100 km/h percorre durante o tempo
de resposta do motorista e calcule a aceleração média imposta ao carro se ele
para totalmente em 5 segundos.
2.
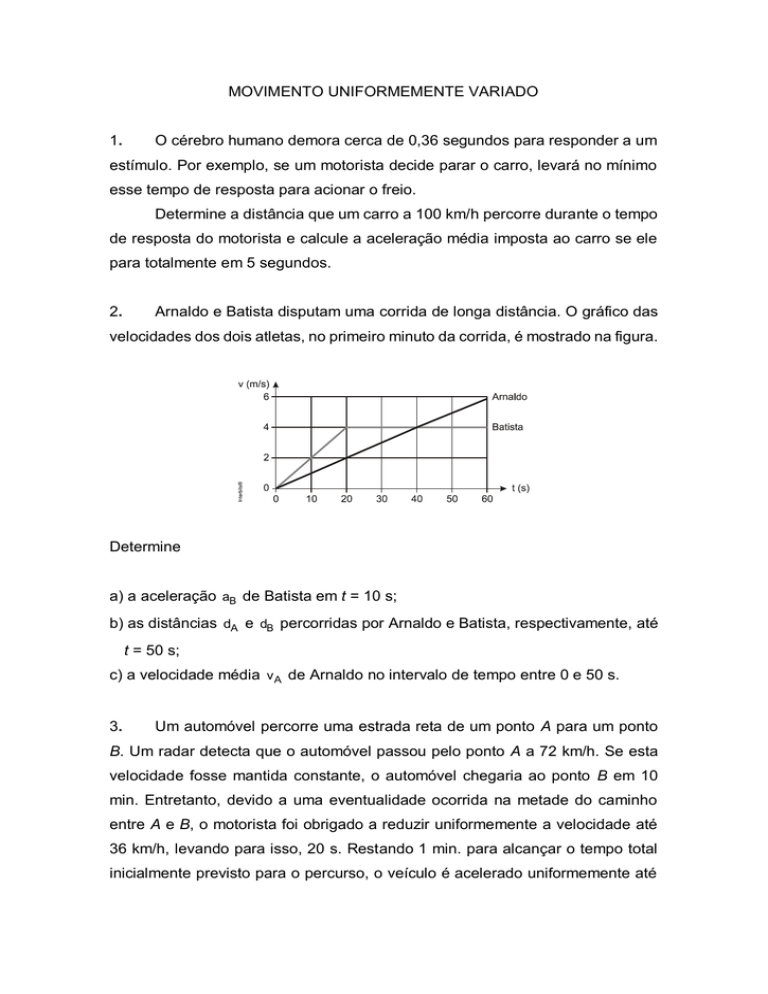
Arnaldo e Batista disputam uma corrida de longa distância. O gráfico das
velocidades dos dois atletas, no primeiro minuto da corrida, é mostrado na figura.
Determine
a) a aceleração aB de Batista em t = 10 s;
b) as distâncias dA e dB percorridas por Arnaldo e Batista, respectivamente, até
t = 50 s;
c) a velocidade média v A de Arnaldo no intervalo de tempo entre 0 e 50 s.
3.
Um automóvel percorre uma estrada reta de um ponto A para um ponto
B. Um radar detecta que o automóvel passou pelo ponto A a 72 km/h. Se esta
velocidade fosse mantida constante, o automóvel chegaria ao ponto B em 10
min. Entretanto, devido a uma eventualidade ocorrida na metade do caminho
entre A e B, o motorista foi obrigado a reduzir uniformemente a velocidade até
36 km/h, levando para isso, 20 s. Restando 1 min. para alcançar o tempo total
inicialmente previsto para o percurso, o veículo é acelerado uniformemente até
108 km/h, levando para isso, 22 s, permanecendo nesta velocidade até chegar
ao ponto B. O tempo de atraso, em segundos, em relação à previsão inicial, é:
a) 46,3
b) 60,0
c) 63,0
d) 64,0
e) 66,7
4.
Uma partícula se move ao longo do eixo x de modo que sua posição é
descrita por x  t   10,0  2,0t  3,0t 2, onde o tempo está em segundos e a posição,
em metros. Calcule o módulo da velocidade média, em metros por segundo, no
intervalo entre t  1,0 s e t  2,0 s.
5.
Duas partículas, a e b, que se movimentam ao longo de um mesmo trecho
retilíneo tem as suas posições (S) dadas em função do tempo (t), conforme o
gráfico abaixo.
O arco de parábola que representa o movimento da partícula b e o
segmento de reta que representa o movimento de a tangenciam-se em t  3 s.
Sendo a velocidade inicial da partícula b de 8 m s, o espaço percorrido pela
partícula a do instante t  0 até o instante t  4 s, em metros, vale
a) 3,0
b) 4,0
c) 6,0
d) 8,0
6.
Um carro está desenvolvendo uma velocidade constante de 72 km h em
uma rodovia federal. Ele passa por um trecho da rodovia que está em obras,
onde a velocidade máxima permitida é de 60 km h. Após 5 s da passagem do
carro, uma viatura policial inicia uma perseguição, partindo do repouso e
desenvolvendo uma aceleração constante. A viatura se desloca 2,1km até
alcançar o carro do infrator. Nesse momento, a viatura policial atinge a
velocidade de
a) 20 m/s
b) 24 m/s
c) 30 m/s
d) 38 m/s
e) 42 m/s
7.
Um automóvel desloca-se por uma estrada retilínea plana e horizontal,
com velocidade constante de módulo v. Após algum tempo, os freios são
acionados e o automóvel percorre uma distância d com as rodas travadas até
parar. Desconsiderando o atrito com o ar, podemos afirmar corretamente que,
se a velocidade inicial do automóvel fosse duas vezes maior, a distância
percorrida seria
a) d/4.
b) d/2.
c) d.
d) 2d.
e) 4d.
8.
Dois carros, A e B, em movimento retilíneo acelerado, cruzam um mesmo
ponto em t = 0 s. Nesse instante, a velocidade v0 de A é igual à metade da de
B, e sua aceleração a corresponde ao dobro da de B.
Determine o instante em que os dois carros se reencontrarão, em função
de v0 e a.
9.
Para garantir a segurança no trânsito, deve-se reduzir a velocidade de um
veículo em dias de chuva, senão vejamos: um veículo em uma pista reta,
asfaltada e seca, movendo-se com velocidade de módulo 36 km h 10 m s é
freado e desloca-se 5,0 m até parar. Nas mesmas circunstâncias, só que com a
pista molhada sob chuva, necessita de 1,0 m a mais para parar.
Considerando a mesma situação (pista seca e molhada) e agora a
velocidade do veículo de módulo 108 km h  30 m s, a alternativa correta que
indica a distância a mais para parar, em metros, com a pista molhada em relação
a pista seca é:
a) 6
b) 2
c) 1,5
d) 9
10.
Um avião vai decolar em uma pista retilínea. Ele inicia seu movimento na
cabeceira da pista com velocidade nula e corre por ela com aceleração média
de 2,0 m/s 2 até o instante em que levanta voo, com uma velocidade de 80 m/s,
antes de terminar a pista.
a) Calcule quanto tempo o avião permanece na pista desde o início do
movimento até o instante em que levanta voo.
b) Determine o menor comprimento possível dessa pista.
11.
Um veículo automotivo, munido de freios que reduzem a velocidade de
5,0m/s, em cada segundo, realiza movimento retilíneo uniforme com velocidade
de módulo igual a 10,0m/s. Em determinado instante, o motorista avista um
obstáculo e os freios são acionados. Considerando-se que o tempo de reação
do motorista é de 0,5s, a distância que o veículo percorre, até parar, é igual, em
m, a
a) 17,0
b) 15,0
c) 10,0
d) 7,0
e) 5,0
12.
Duas partículas, A e B,
que
executam movimentos retilíneos
uniformemente variados, se encontram em t = 0 na mesma posição. Suas
velocidades, a partir desse instante, são representadas pelo gráfico abaixo.
As acelerações experimentadas por A e B têm o mesmo módulo de
0,2m s2 . Com base nesses dados, é correto afirmar que essas partículas se
encontrarão novamente no instante
a) 10 s
b) 50 s
c) 100 s
d) 500 s
13.
Os vencedores da prova de 100 m rasos são chamados de homem/mulher
mais rápidos do mundo. Em geral, após o disparo e acelerando de maneira
constante, um bom corredor atinge a velocidade máxima de 12,0 m/s a 36,0 m
do ponto de partida. Esta velocidade é mantida por 3,0 s. A partir deste ponto, o
corredor desacelera, também de maneira constante, com a = − 0,5 m/s 2,
completando a prova em, aproximadamente, 10 s. É correto afirmar que a
aceleração nos primeiros 36,0 m, a distância percorrida nos 3,0 s seguintes e
a velocidade final do corredor ao cruzar a linha de chegada são,
respectivamente:
a) 2,0 m/s2; 36,0 m; 10,8 m/s.
b) 2,0 m/s2; 38,0 m; 21,6 m/s.
c) 2,0 m/s2; 72,0 m; 32,4 m/s.
d) 4,0 m/s2; 36,0 m; 10,8 m/s.
e) 4,0 m/s2; 38,0 m; 21,6 m/s.
14.
Em uma prova internacional de ciclismo, dois dos ciclistas, um francês e,
separado por uma distância de 15 m à sua frente, um inglês, se movimentam
com velocidades iguais e constantes de módulo 22 m/s. Considere agora que o
representante brasileiro na prova, ao ultrapassar o ciclista francês, possui uma
velocidade constante de módulo 24 m/s e inicia uma aceleração constante de
módulo 0,4 m/s 2, com o objetivo de ultrapassar o ciclista inglês e ganhar a prova.
No instante em que ele ultrapassa o ciclista francês, faltam ainda 200 m para a
linha de chegada. Com base nesses dados e admitindo que o ciclista inglês, ao
ser ultrapassado pelo brasileiro, mantenha constantes as características do seu
movimento, assinale a alternativa correta para o tempo gasto pelo ciclista
brasileiro para ultrapassar o ciclista inglês e ganhar a corrida.
a) 1 s.
b) 2 s.
c) 3 s.
d) 4 s.
e) 5 s.
15.
A Copa do Mundo é o segundo maior evento desportivo do mundo, ficando
atrás apenas dos Jogos Olímpicos. Uma das regras do futebol que gera polêmica
com certa frequência é a do impedimento. Para que o atacante A não esteja em
impedimento, deve haver ao menos dois jogadores adversários a sua frente, G
e Z, no exato instante em que o jogador L lança a bola para A (ver figura).
Considere que somente os jogadores G e Z estejam à frente de A e que somente
A e Z se deslocam nas situações descritas a seguir.
a) Suponha que a distância entre A e Z seja de 12 m. Se A parte do repouso em
direção ao gol com aceleração de 3,0 m/s2 e Z também parte do repouso com
a mesma aceleração no sentido oposto, quanto tempo o jogador L tem para
lançar a bola depois da partida de A antes que A encontre Z?
b) O árbitro demora 0,1 s entre o momento em que vê o lançamento de L e o
momento em que determina as posições dos jogadores A e Z. Considere agora
que A e Z movem-se a velocidades constantes de 6,0 m/s, como indica a
figura. Qual é a distância mínima entre A e Z no momento do lançamento para
que o árbitro decida de forma inequívoca que A não está impedido?
16.
Um motorista dirige um carro com velocidade constante de 80 km/h, em
linha reta, quando percebe uma “lombada” eletrônica indicando a velocidade
máxima permitida de 40 km/h. O motorista aciona os freios, imprimindo uma
desaceleração constante, para obedecer à sinalização e passar pela “lombada”
com a velocidade máxima permitida. Observando-se a velocidade do carro em
função do tempo, desde o instante em que os freios foram acionados até o
instante de passagem pela “lombada”, podemos traçar o gráfico a seguir.
Determine a distância percorrida entre o instante t = 0, em que os freios
foram acionados, e o instante t = 3,0 s, em que o carro ultrapassa a “lombada”.
Dê sua resposta em metros.
17.
O gráfico em função do tempo mostra dois carros A e B em movimento
retilíneo.
Em t = 0 s os carros estão na mesma posição.
Com base na análise do gráfico, é correto afirmar.
a) Os carros vão estar na mesma posição nos instantes t = 0 s e t = 4,0
b) Os carros não vão se encontrar após t = 0, porque a velocidade de A é maior
que a do carro B
c) Os carros vão se encontrar novamente na posição S = 10 m
d) Os carros não vão se encontrar, porque estão em sentidos contrários.
e) Os instantes em que os carros vão estar na mesma posição é t = 0 s e t = 8,0s
18.
Dois automóveis A e B se movimentam sobre uma mesma trajetória
retilínea, com suas velocidades variando com o tempo de acordo com o gráfico
a seguir. Sabe-se que esses móveis se encontram no instante 10 s. A distância
entre eles, no instante inicial (t = 0 s), era de
a) 575 m
b) 425 m
c) 375 m
d) 275 m
e) 200 m
19.
Um motorista conduz seu automóvel pela BR-277 a uma velocidade de
108 km/h quando avista uma barreira na estrada, sendo obrigado a frear
(desaceleração de 5 m/s2) e parar o veículo após certo tempo. Pode-se afirmar
que o tempo e a distância de frenagem serão, respectivamente:
a) 6 s e 90 m.
b) 10 s e 120 m.
c) 6 s e 80 m.
d) 10 s e 200 m.
e) 6 s e 120 m.
20.
Um corredor olímpico de 100 metros rasos acelera desde a largada, com
aceleração constante, até atingir a linha de chegada, por onde ele passará com
velocidade instantânea de 12 m/s no instante final. Qual a sua aceleração
constante?
a) 10,0 m/s2
b) 1,0 m/s2
c) 1,66 m/s2
d) 0,72 m/s2
e) 2,0 m/s2
21.
Em uma região plana, delimitou-se o triângulo ABC, cujos lados AB e BC
medem, respectivamente, 300,00 m e 500,00 m. Duas crianças, de 39,20 kg
cada uma, partem, simultaneamente, do repouso, do ponto A, e devem chegar
juntas ao ponto C, descrevendo movimentos retilíneos uniformemente
acelerados.
Para que logrem êxito, é necessário que a razão entre as acelerações
escalares, a1 e a2, das respectivas crianças, seja
a)
a1 7

a2 8
b)
a1 8

a2 7
c)
a1 7

a2 5
d)
a1 5

a2 7
e)
a1 583

a2 800
22.
Os avanços tecnológicos nos meios de transporte reduziram de forma
significativa o tempo de viagem ao redor do mundo. Em 2008 foram
comemorados os 100 anos da chegada em Santos do navio "Kasato Maru", que,
partindo de Tóquio, trouxe ao Brasil os primeiros imigrantes japoneses. A viagem
durou cerca de 50 dias. Atualmente, uma viagem de avião entre São Paulo e
Tóquio dura em média 24 horas. A velocidade escalar média de um avião
comercial no trecho São Paulo - Tóquio é de 800 km/h.
a) O comprimento da trajetória realizada pelo "Kasato Maru" é igual a
aproximadamente duas vezes o comprimento da trajetória do avião no trecho
São Paulo-Tóquio. Calcule a velocidade escalar média do navio em sua viagem
ao Brasil.
b) A conquista espacial possibilitou uma viagem do homem à Lua realizada em
poucos dias e proporcionou a máxima velocidade de deslocamento que um ser
humano já experimentou. Considere um foguete subindo com uma aceleração
resultante constante de módulo aR = 10 m/s 2 e calcule o tempo que o foguete
leva para percorrer uma distância de 800 km, a partir do repouso.
23.
Um avião a jato, para transporte de passageiros, precisa atingir a
velocidade de 252 km/h para decolar em uma pista plana e reta. Para uma
decolagem segura, o avião, partindo do repouso, deve percorrer uma distância
máxima de 1 960 m até atingir aquela velocidade. Para tanto, os propulsores
devem imprimir ao avião uma aceleração mínima e constante de:
a) 1,25 m/s2.
b) 1,40 m/s2.
c) 1,50 m/s2.
d) 1,75 m/s2.
e) 2,00 m/s2.
24.
Uma possível solução para a crise do tráfego aéreo no Brasil envolve o
emprego de um sistema de trens de alta velocidade conectando grandes
cidades. Há um projeto de uma ferrovia de 400 km de extensão que interligará
as cidades de São Paulo e Rio de Janeiro por trens que podem atingir até 300
km/h.
a) Para ser competitiva com o transporte aéreo, estima-se que a viagem de trem
entre essas duas cidades deve durar, no máximo, 1 hora e 40 minutos. Qual é
a velocidade média de um trem que faz o percurso de 400 km nesse tempo?
b) Considere um trem viajando em linha reta com velocidade constante. A uma
distância de 30 km do final do percurso, o trem inicia uma desaceleração
uniforme de 0,06 m/s 2, para chegar com velocidade nula a seu destino. Calcule
a velocidade do trem no início da desaceleração.
25.
Um corredor de 100 metros rasos, ao cruzar exatamente a marca de 50,0
m, tem uma velocidade instantânea de 10,0 m/s. Nesse instante começa a soprar
um vento contrário que cria uma aceleração total de - 0,36 m/s2 sobre o atleta.
Qual a velocidade do atleta ao cruzar a faixa de chegada?
a) 10,0 m/s
b) 9,0 m/s
c) 8,0 m/s
d) 12,0 m/s
e) 14,0 m/s
26.
O engavetamento é um tipo comum de acidente que ocorre quando
motoristas deliberadamente mantêm uma curta distância do carro que se
encontra à sua frente e este último repentinamente diminui sua velocidade. Em
um trecho retilíneo de uma estrada, um automóvel e o caminhão, que o segue,
trafegam no mesmo sentido e na mesma faixa de trânsito, desenvolvendo,
ambos, velocidade de 108 km/h. Num dado momento, os motoristas veem um
cavalo entrando na pista. Assustados, pisam simultaneamente nos freios de
seus veículos aplicando, respectivamente, acelerações de intensidades 3 m/s 2 e
2 m/s2. Supondo desacelerações constantes, a distância inicial mínima de
separação entre o para-choque do carro (traseiro) e o do caminhão (dianteiro),
suficiente para que os veículos parem, sem que ocorra uma colisão, é, em m, de
a) 50.
b) 75.
c) 100.
d) 125.
e) 150.
27.
A pista principal do aeroporto de Congonhas em São Paulo media 1.940
m de comprimento no dia do acidente aéreo com o Airbus 320 da TAM, cuja
velocidade tanto para pouso quanto para decolagem é 259,2 km/h. Após
percorrer 1.240 m da pista o piloto verificou que a velocidade da aeronave era
de 187,2 km/h. Mantida esta desaceleração, a que distância do fim da pista o
piloto deveria arremeter a aeronave, com aceleração máxima de 4 m/s 2, para
evitar o acidente?
a) 312 m
b) 390 m
c) 388 m
d) 648 m
e) 700 m
28.
Uma partícula puntiforme tem, em certo instante t, a velocidade, em m/s,
dada por v0 = 1,0 i - 2,0 j + 5,0 k. Dois segundos depois, sua velocidade, em m/s,
é dada por v2 = 4,0 i - 2,0 j + 1,0 k. No intervalo de tempo considerado, o módulo
da aceleração média, em m/s2, é:
a) 25,0
b) 5,0
c) 1,0
d) 2,5
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Desde Aristóteles, o problema da queda dos corpos é um dos mais
fundamentais da ciência. Como a observação e a medida diretas do movimento
de corpos em queda livre eram difíceis de realizar, Galileu decidiu usar um plano
inclinado, onde poderia estudar o movimento de corpos sofrendo uma
aceleração mais gradual do que a da gravidade.
MICHEL RIVAL
Adaptado de Os grandes experimentos científicos. Rio de Janeiro: Jorge Zahar,
1997.
Observe, a seguir, a reprodução de um plano inclinado usado no final do
século XVIII para demonstrações em aula.
Admita que um plano inclinado M1, idêntico ao mostrado na figura, tenha
altura igual a 1,0m e comprimento da base sobre o solo igual a 2,0m. Uma
pequena caixa é colocada, a partir do repouso, no topo do plano inclinado M1 e
desliza praticamente sem atrito até a base.
Em seguida, essa mesma caixa é colocada, nas mesmas condições, no
topo de um plano inclinado M2, com a mesma altura de M1 e comprimento da
base sobre o solo igual a 3,0m.
29.
A razão t1/t2 entre os tempos de queda da caixa após deslizar,
respectivamente, nos planos M1 e M2 , é igual a:
a) 2
b)
2
c) 1
d)
1
2
30.
A razão v1/v2 entre as velocidades da caixa ao alcançar o sol o após
deslizar, respectivamente, nos planos M1 e M2, é igual a:
a) 2
b)
2
c) 1
d)
2
31.
Um corredor velocista corre a prova dos 100 m rasos em,
aproximadamente, 10 s. Considerando-se que o corredor parte do repouso,
tendo aceleração constante, e atinge sua velocidade máxima no final dos 100 m,
a aceleração do corredor durante a prova em m/s2 é:
a) 1,0
b) 2,0
c) 3,0
d) 4,0
e) 5,0
32.
Considere o movimento de um caminhante em linha reta. Este caminhante
percorre os 20,0 s iniciais à velocidade constante v 1 = 2,0 m/s. Em seguida, ele
percorre os próximos 8,0 s com aceleração constante a = 1 m/s 2 (a velocidade
inicial é 2,0 m/s). Calcule:
a) a distância percorrida nos 20,0 s iniciais;
b) a distância percorrida nos 28,0 s totais;
c) a velocidade final do caminhante.
33.
Um esquiador, partindo do repouso do ponto A da rampa, passa pelo
ponto B com velocidade de módulo 5 m/s. Considerando constante a aceleração
do esquiador, sua velocidade, no ponto C, será:
a) √75 m/s
b) 10 m/s
c) 15 m/s
d) 20 m/s
e) 25 m/s
34.
Em muitas praças de pedágio de rodovias existe um sistema que permite
a abertura automática da cancela. Ao se aproximar, um veículo munido de um
dispositivo apropriado é capaz de trocar sinais eletromagnéticos com outro
dispositivo na cancela. Ao receber os sinais, a cancela abre-se automaticamente
e o veículo é identificado para posterior cobrança. Para as perguntas a seguir,
desconsidere o tamanho do veículo.
a) Um veículo aproxima-se da praça de pedágio a 40 km/h. A cancela recebe os
sinais quando o veículo se encontra a 50 m de distância. Qual é o tempo
disponível para a completa abertura da cancela?
b) O motorista percebe que a cancela não abriu e aciona os freios exatamente
quando o veículo se encontra a 40 m da mesma, imprimindo uma
desaceleração de módulo constante. Qual deve ser o valor dessa
desaceleração para que o veículo pare exatamente na cancela?
35.
Um carro viajando em uma estrada retilínea e plana com uma velocidade
constante V1 = 72km/h passa por outro que está em repouso no instante t = 0 s.
O segundo carro acelera para alcançar o primeiro com aceleração a 2 = 2,0m/s2.
O tempo que o segundo carro leva para atingir a mesma velocidade do primeiro
é:
a) 1,0 s.
b) 2,0 s.
c) 5,0 s.
d) 10,0 s.
e) 20,0 s.
36.
Um atleta corre a uma certa velocidade constante em linha reta e
ultrapassa um carro que está sendo acelerado (a = 2,0 m/s 2) do repouso na
mesma direção e sentido. O instante de tempo t = 0 é o tempo inicial de
aceleração do carro e também o instante de tempo em que o atleta passa pelo
carro. O atleta consegue se manter à frente do carro por 3,0 s. Qual é a
velocidade do atleta?
a) 1,0 m/s
b) 3,0 m/s
c) 7,0 m/s
d) 9,0 m/s
e) 11,0 m/s
37.
Um corredor de 100 metros rasos percorre os 20 primeiros metros da
corrida em 4,0 s com aceleração constante. A velocidade atingida ao final dos
4,0 s é então mantida constante até o final da corrida.
a) Qual é a aceleração do corredor nos primeiros 20 m da corrida?
b) Qual é a velocidade atingida ao final dos primeiros 20m?
c) Qual é o tempo total gasto pelo corredor em toda a prova?
38.
Em uma prova de atletismo, um corredor de 100m rasos parte do repouso,
corre com aceleração constante nos primeiros 50 m e depois mantém a
velocidade constante até o final da prova. Sabendo que a prova foi completada
em 10 s, o valor da aceleração é:
a) 2,25 m/s2.
b) 1,00 m/s2.
c) 1,50 m/s2.
d) 3,20 m/s2.
e) 2,50 m/s2.
39.
A velocidade máxima permitida em uma autoestrada é de 110 km/h
(aproximadamente 30 m/s) e um carro, nessa velocidade, leva 6s para parar
completamente. Diante de um posto rodoviário, os veículos devem trafegar no
máximo a 36 km/h (10 m/s). Assim, para que carros em velocidade máxima
consigam obedecer o limite permitido, ao passar em frente do posto, a placa
referente à redução de velocidade deverá ser colocada antes do posto, a uma
distância, pelo menos, de
a) 40 m
b) 60 m
c) 80 m
d) 90 m
e) 100 m
40.
Um avião de vigilância aérea está voando a uma altura de 5,0 km, com
velocidade de 50 10 m/s no rumo norte, e capta no radiogoniômetro um sinal de
socorro vindo da direção noroeste, de um ponto fixo no solo. O piloto então liga
o sistema de pós-combustão da turbina, imprimindo uma aceleração constante
de 6,0 m/s2. Após 40
10
s, mantendo a mesma direção, ele agora constata que
3
o sinal está chegando da direção oeste. Neste instante, em relação ao avião, o
transmissor do sinal se encontra a uma distância de
a) 5,2 km
b) 6,7 km
c) 12 km
d) 13 km
e) 28 km
41.
Em um piso horizontal um menino dá um empurrão em seu
caminhãozinho de plástico. Assim que o contato entre o caminhãozinho e a mão
do menino é desfeito, observa-se que em um tempo de 6 s o brinquedo foi capaz
de percorrer uma distância de 9 m até cessar o movimento. Se a resistência
oferecida ao movimento do caminhãozinho se manteve constante, a velocidade
inicial obtida após o empurrão, em m/s, foi de
a) 1,5.
b) 3,0.
c) 4,5.
d) 6,0.
e) 9,0.
42.
Em algumas rodovias, em trechos retilíneos que antecedem cruzamentos
ou curvas perigosas, a fim de induzir o motorista à diminuição de sua velocidade
até um valor mais seguro, é aplicada em relevo sobre o asfalto uma sequência
de estreitas faixas perpendiculares ao traçado da pista, conhecidas por
sonorizadores. Ao serem transpostos, os sonorizadores produzem o peculiar
som "TRUNTRUM". Quando o motorista está consciente de que deve diminuir
sua velocidade e o faz com a devida desaceleração, o intervalo de tempo entre
um "TRUNTRUM" e o próximo é igual, quaisquer que sejam as duas faixas
consecutivas transpostas. Se, contudo, o motorista não diminui a velocidade, os
intervalos de tempo entre um som e o próximo começam a ficar
progressivamente menores, comunicando sonoramente a iminência do perigo.
Uma sequência de sete sonorizadores foi aplicada sobre uma rodovia, em um
trecho no qual a velocidade deveria ser reduzida de 34 m/s para 22 m/s
(aproximadamente, 120 km/h para 80 km/h). No projeto, a expectativa de tempo
e velocidade em todo o trecho foi tabelada relativamente ao primeiro sonorizador.
Uma vez que foram distribuídas sete faixas sonorizadoras, de forma que a cada
segundo, para um motorista que esteja obedecendo à sinalização, o veículo
passa sobre uma delas, responda.
a) Em termos das expressões usadas para classificar a velocidade e a
aceleração em movimentos retilíneos uniformemente variados, escreva as duas
possíveis classificações para o movimento de um veículo que inicia a passagem
dessa sequência de sonorizadores.
b) Deixando expresso seu raciocínio, calcule a distância em metros, do primeiro
ao sétimo sonorizador.
43.
Um jogador de futebol em repouso vê uma bola passar por ele a uma
velocidade constante de 5m/s. Ele sai em perseguição da mesma com uma
aceleração constante igual a 1,0 m/s2.
a) Em quanto tempo ele alcançará a bola?
b) Qual a distância percorrida por jogador e bola, quando o jogador finalmente
alcançar a bola?
44.
Um carro corre a uma velocidade de 20 m/s quando o motorista vê um
obstáculo 50 m à sua frente.
A desaceleração mínima constante que deve ser dada ao carro para que
não haja choque, em m/s 2, é de
a) 4,0
b) 2,0
c) 1,0
d) 0,5
45.
Um veículo em movimento sofre uma desaceleração uniforme em uma
pista reta, até parar. Sabendo-se que, durante os últimos 9,0 m de seu
deslocamento, a sua velocidade diminui 12 m/s, calcule o módulo da
desaceleração imposta ao veículo, em m/s2.
46.
Ao perceber o sinal vermelho, um motorista, cujo carro trafegava a 80
km/h, pisa no freio e para em 10 s.
A
desaceleração
média
do
veículo,
em
km/h 2,
equivale,
aproximadamente, a:
a) 1,4 × 103
b) 8,0 × 103
c) 1,8 × 104
d) 2,9 × 104
47.
Um predador, partindo do repouso, alcança sua velocidade máxima de 54
km/h em 4 s e mantém essa velocidade durante 10 s. Se não alcançar sua presa
nesses 14 s, o predador desiste da caçada. A presa, partindo do repouso,
alcança sua velocidade máxima, que é 4/5 da velocidade máxima do predador,
em 5 s e consegue mantê-la por mais tempo que o predador. Suponha-se que
as acelerações são constantes, que o início do ataque e da fuga são simultâneos
e que predador e presa partem do repouso. Para o predador obter sucesso em
sua caçada, a distância inicial máxima entre ele e a presa é de:
a) 21 m
b) 30 m
c) 42 m
d) 72 m
e) 80 m
48.
Um automóvel que trafega com velocidade constante de 10 m/s, em uma
pista reta e horizontal, passa a acelerar uniformemente à razão de 60 m/s em
cada minuto, mantendo essa aceleração durante meio minuto. A velocidade
instantânea do automóvel, ao final desse intervalo de tempo, e sua velocidade
média, no mesmo intervalo de tempo, são, respectivamente:
a) 30 m/s e 15 m/s.
b) 30 m/s e 20 m/s.
c) 20 m/s e 15 m/s.
d) 40 m/s e 20 m/s.
e) 40 m/s e 25 m/s.
49.
Uma ambulância desloca-se a 108 km/h num trecho plano de uma rodovia
quando um carro, a 72 km/h, no mesmo sentido da ambulância, entra na sua
frente a 100 m de distância, mantendo sua velocidade constante. A mínima
aceleração, em m/s2, que a ambulância deve imprimir para não se chocar com o
carro é, em módulo, pouco maior que
a) 0,5.
b) 1,0.
c) 2,5.
d) 4,5.
e) 6,0.
50.
Durante um experimento, um pesquisador anotou as posições de dois
móveis A e B, elaborando a tabela a seguir.
O movimento de A é uniforme e o de B é uniformemente variado.
A aceleração do móvel B é, em m/s 2, igual a:
a) 2,5
b) 5,0
c) 10,0
d) 12,5
51.
Durante um experimento, um pesquisador anotou as posições de dois
móveis A e B, elaborando a tabela a seguir.
O movimento de A é uniforme e o de B é uniformemente variado.
A distância, em metros, entre os móveis A e B, no instante t=6 segundos,
corresponde a:
a) 45
b) 50
c) 55
d) 60
52.
Uma norma de segurança sugerida pela concessionária de uma
autoestrada recomenda que os motoristas que nela trafegam mantenham seus
veículos separados por uma "distância" de 2,0 segundos.
a) Qual é essa distância, expressa adequadamente em metros para veículos que
percorrem a estrada com a velocidade constante de 90km/h?
b) Suponha que, nessas condições, um motorista freie bruscamente seu veículo
até parar, com aceleração constante de módulo 5,0m/s 2, e o motorista de trás só
reaja, freando seu veículo, depois de 0,50s. Qual deve ser a aceleração mínima
do veículo de trás para não colidir com o da frente?
53.
Um partícula se move em uma reta com aceleração constante. Sabe-se
que no intervalo de tempo de 10s ela passa duas vezes pelo mesmo ponto dessa
reta, com velocidades de mesmo módulo, v=4,0m/s, em sentidos opostos. O
módulo do deslocamento e o espaço percorrido pela partícula nesse intervalo de
tempo são, respectivamente,
a) 0,0 m e 10 m.
b) 0,0 m e 20 m.
c) 10 m e 5,0 m.
d) 10 m e 10 m.
e) 20 m e 20 m.
54.
Ao iniciar a travessia de um túnel retilíneo de 200 metros de comprimento,
um automóvel de dimensões desprezíveis movimenta-se com velocidade de
25m/s. Durante a travessia, desacelera uniformemente, saindo do túnel com
velocidade de 5m/s.
O módulo de sua aceleração escalar, nesse percurso, foi de
a) 0,5 m/s2
b) 1,0 m/s2
c) 1,5 m/s2
d) 2,0 m/s2
e) 2,5 m/s2
55.
Um automóvel parte do repouso no instante t=0 e acelera uniformemente
com 5,0m/s2, durante 10s. A velocidade escalar média do automóvel entre os
instantes t=6,0s e t=10s, em m/s, foi de
a) 40
b) 35
c) 30
d) 25
e) 20
56.
Um automóvel trafega com velocidade constante de 12m/s por uma
avenida e se aproxima de um cruzamento onde há um semáforo com fiscalização
eletrônica. Quando o automóvel se encontra a uma distância de 30m do
cruzamento, o sinal muda de verde para amarelo. O motorista deve decidir entre
parar o carro antes de chegar ao cruzamento ou acelerar o carro e passar pelo
cruzamento antes do sinal mudar para vermelho. Este sinal permanece amarelo
por 2,2 s. O tempo de reação do motorista (tempo decorrido entre o momento
em que o motorista vê a mudança de sinal e o momento em que realiza alguma
ação) é 0,5s.
a) Determine a mínima aceleração constante que o carro deve ter para parar
antes de atingir o cruzamento e não ser multado.
b) Calcule a menor aceleração constante que o carro deve ter para passar pelo
cruzamento sem ser multado. Aproxime 1,7 2≈3,0.
57.
Ao executar um salto de abertura retardada, um para-quedista abre seu
para-quedas depois de ter atingido a velocidade, com direção vertical, de 55m/s.
Após 2s, sua velocidade cai para 5m/s.
a) Calcule o módulo da aceleração média do para-quedista nesses 2s.
b) Sabendo que a massa do para-quedista é 80kg, calcule o módulo da força de
tração média resultante nas cordas que sustentam o para-quedista durante
esses 2s.
(Despreze o atrito do ar sobre o para-quedista e considere g=10m/s2.)
58.
Um carro está viajando numa estrada retilínea com a velocidade de
72km/h. Vendo adiante um congestionamento no trânsito, o motorista aplica os
freios durante 2,5s e reduz a velocidade para 54km/h. Supondo que a aceleração
é constante durante o período de aplicação dos freios, calcule o seu módulo, em
m/s2.
a) 1,0
b) 1,5
c) 2,0
d) 2,5
e) 3,0
59.
Uma bola cai verticalmente, atinge o solo com velocidade de 10m/s, e
retorna na vertical com velocidade de 5,0m/s. Se a bola esteve em contato com
o solo durante 0,10s, pode-se afirmar que o módulo da aceleração média durante
esse tempo vale
a) 1,5.101 m/s2
b) 1,5.102 m/s2
c) 2,5.101 m/s2
d) 5,0.101 m/s2
e) 5,0.102 m/s2
60.
Numa competição automobilística, um carro se aproxima de uma curva
em grande velocidade. O piloto, então, pisa o freio durante 4s e consegue reduzir
a velocidade do carro para 30m/s. Durante a freada o carro percorre 160m.
Supondo que os freios imprimam ao carro uma aceleração retardadora
constante, calcule a velocidade do carro no instante em que o piloto pisou o freio.
Gabarito:
1:  D = 10 m e a = - 5,6 m/s2
2:
a) aB = 0,2 m/s2
b) dA = 125 m e dB = 160 m
c) vA = 2,5 m/s
3:
[D]
4:
11 m/s.
5:
[D]
6:
[E]
7:
[E]
8:
t = 4Vo/a
9:
[D]
10:
a) 40 s
b) 1.600 m
11:
[B]
12:
[D]
13:
[A]
14:
[E]
15:
a) D = 12 m.
b) Dmín = 1,2 m
16:
50 metros
17:
[A]
18:
[A]
19:
[A]
20:
[D]
21:
[A]
22:
a) 32 km/h
b) 400 s
23:
[A]
24:
a) 240 km/h
b) 60 m/s
25:
[C]
26:
[B]
27:
[C]
28:
[D]
29:
[D]
30:
[C]
31:
[B]
32:
a) 40 m
b) 88,0 m
c) 10 m/s
33:
[D]
34:
a) 4,5 s
b) 1,54 m/s2
35:
[D]
36:
[B]
37:
a) γ = 2,5m/s2
b) Vf = 10m/s
c) T = 12,0s
38:
[A]
39:
[C]
40:
[D]
41:
[B]
42:
a)
1) Considerando que a velocidade é positiva o movimento é
progressivo.
2) Na medida em que o módulo ou intensidade da velocidade está
diminuindo o movimento é retardado.
b) 168 m
43:
a) t = 10 s
b) 50 m
44:
[A]
45:
8 m/s2.
46:
[D]
47:
[C]
48:
[E]
49:
[A]
50:
[C]
51:
[B]
52:
a) 50 m
b) 3,125 m/s2 (em módulo)
53:
[B]
54:
[C]
55:
[A]
56:
a) a = -3 m/s2
b) a ≈ 2,4 m/s2
57:
a) 25 m/s2
b) 2800 N
58:
[C]
59:
[B]
60:
v0 = 50 m/s