Microsoft PowerPoint - 11.Vasos de Press\343o e

EM 423 RESISTÊNCIA DOS MATERIAIS
EM 423 RESISTÊNCIA DOS MATERIAIS
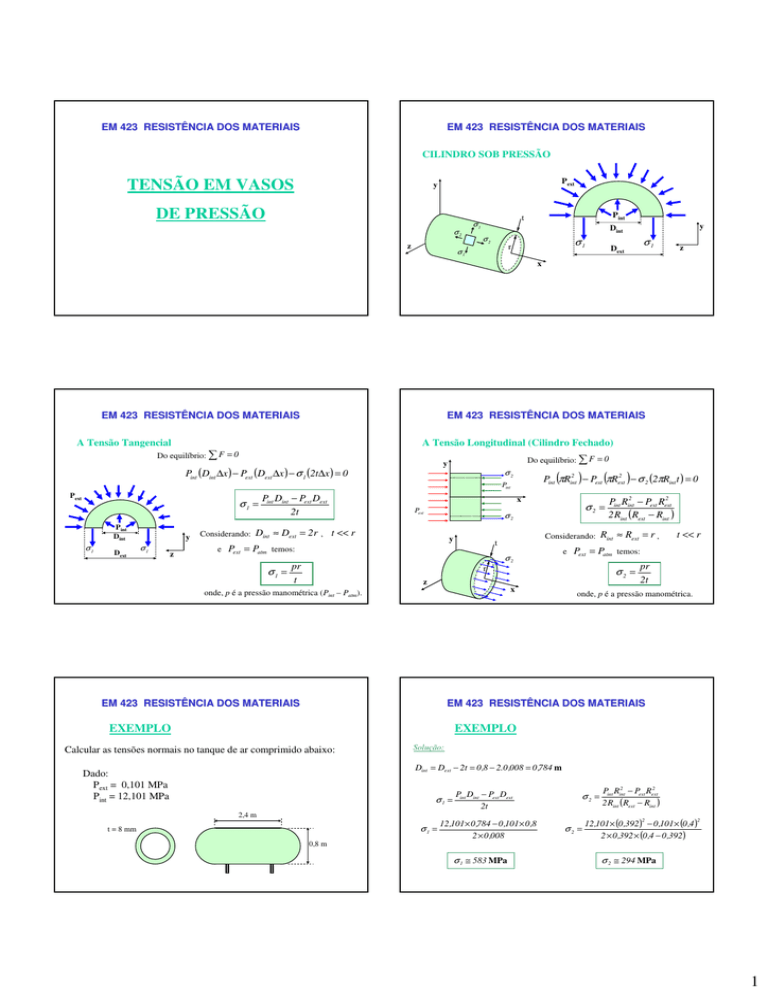
CILINDRO SOB PRESSÃO
TENSÃO EM VASOS
Pext
y
DE PRESSÃO
σ2
z
Pint
t
σ1
y
Dint
σ2
σ1
r
σ1
σ1
Dext
z
x
EM 423 RESISTÊNCIA DOS MATERIAIS
EM 423 RESISTÊNCIA DOS MATERIAIS
A Tensão Tangencial
A Tensão Longitudinal (Cilindro Fechado)
Do equilíbrio: ∑ F = 0
Do equilíbrio: ∑ F = 0
y
Pint (Dint ∆x ) − Pext (Dext ∆x ) − σ 1 (2t∆x ) = 0
σ2
(
Pext
σ1 =
Pint
Dint
σ1
Dext
y
σ1
z
Considerando:
e
Pint Dint − Pext Dext
2t
x
Pext
Dint ≈ Dext = 2 r , t << r
(
σ2 =
σ2
Considerando:
y
t
Pext = Patm temos:
σ2
pr
σ1 =
t
)
e
EM 423 RESISTÊNCIA DOS MATERIAIS
Rint ≈ Rext = r ,
σ2 =
x
onde, p é a pressão manométrica (Pint – Patm).
2
2
Pint Rint
− Pext Rext
2 Rint (Rext − Rint )
t << r
Pext = Patm temos:
r
z
)
2
2
Pint πRint
− Pext πRext
− σ 2 (2πRint t ) = 0
Pint
pr
2t
onde, p é a pressão manométrica.
EM 423 RESISTÊNCIA DOS MATERIAIS
EXEMPLO
EXEMPLO
Calcular as tensões normais no tanque de ar comprimido abaixo:
Solução:
Dint = Dext − 2t = 0 ,8 − 2.0 ,008 = 0 ,784 m
Dado:
Pext = 0,101 MPa
Pint = 12,101 MPa
σ1 =
Pint Dint − Pext Dext
2t
σ2 =
2,4 m
σ1 =
t = 8 mm
12 ,101 × 0 ,784 − 0 ,101 × 0 ,8
2 × 0 ,008
2
2
Pint Rint
− Pext Rext
2 Rint (Rext − Rint )
12 ,101 × (0 ,392) − 0 ,101 × (0 ,4 )
2 × 0 ,392 × (0 ,4 − 0 ,392)
2
σ2 =
2
0,8 m
σ 1 ≅ 583 MPa
σ 2 ≅ 294 MPa
1
EM 423 RESISTÊNCIA DOS MATERIAIS
EM 423 RESISTÊNCIA DOS MATERIAIS
TRAÇÃO: Placa com Furo no Centro
Concentração de tensão ocorre nas proximidades de uma descontinuidade
geométrica (ex. eixo escalonado) e aparecem também em pontos de
carregamento (ex. carga aplicada por um pino de conexão).
CONCENTRAÇÃO
DE TENSÃO
K=
σ max
σ méd
σméd
EM 423 RESISTÊNCIA DOS MATERIAIS
TRAÇÃO: Eixo Escalonado
EM 423 RESISTÊNCIA DOS MATERIAIS
TORÇÃO
σméd
EM 423 RESISTÊNCIA DOS MATERIAIS
EXEMPLO
FLEXÃO PURA
A concentração de tensão pode acorrer:
• Nas vizinhanças onde carregamentos são aplicados
• Nas vizinhanças de mudanças bruscas na seção transversal
EM 423 RESISTÊNCIA DOS MATERIAIS
Mc
σm = K
I
Uma barra chata de aço é constituída de duas partes de 10 mm de
espessura, uma com 40 mm e outra com 60 mm de largura, ligadas
por uma região de transição com arredondamento de 8 mm de raio
(r). Determinar a máxima carga axial P que pode ser suportada
com segurança pela barra sendo a tensão admissível do material
de σadm = 165 MPa.
r
2
EM 423 RESISTÊNCIA DOS MATERIAIS
EM 423 RESISTÊNCIA DOS MATERIAIS
EXEMPLO
EXEMPLO
Solução:
D 60 mm
=
= 1,5
d 40 mm
r
8 mm
=
= 0 ,2
d 40 mm
K = 1,82
σ med =
σ med =
σ adm
1,82
=
165 MPa
= 90 ,7 MPa
1,82
P
Amenor
∴ P = Amenor ⋅ σ med = 40 ⋅ 10 ⋅ 90 ,7 = 36 ,3 kN
EM 423 RESISTÊNCIA DOS MATERIAIS
EM 423 RESISTÊNCIA DOS MATERIAIS
EXEMPLO
EXEMPLO
Um eixo de aço de seção circular é constituído de duas partes,
uma com 10 cm e outra com 15 cm de diâmetro, ligadas por uma
região de transição com arredondamento de 0,5 cm de raio (r).
Determinar a máxima carga axial P que pode ser suportada,
sendo a tensão de escoamento do material de σesc = 495 MPa.
Considerar um fator de segurança igual a 3,0.
EM 423 RESISTÊNCIA DOS MATERIAIS
EXEMPLO
Solução:
Kt = 2,35
D 0 ,15 m
=
= 1,5
d 0 ,10 m
σ med =
r 0 ,005 m
=
= 0 ,05
d 0 ,10 m
1 σ esc
1 495 MPa
=
K t CS y 2 ,35
3
σ med = 70 ,21 MPa
∴ P = Amenor ⋅ σ med =
π ⋅ 0 ,12
4
⋅70 ,21 ⋅ 106
∴ P = 551,45 kN
3