junção pn com polarização direta

DIODOS
FUNDAMENTOS
12 h
DIODO IDEAL
2
LIMITAÇÃO DA TENSÃO DIRETA
E CORRENTE REVERSA
3
RETIFICADOR
4
EXEMPLO 3.1
Considere o circuito a seguir, onde a tensão
da bateria é de 12 V e a tensão de pico da
senóide é de 24 V.
 Determine a fração de tempo de cada ciclo
em que o diodo conduz, e também o valor
de pico da corrente no diodo e a tensão de
polarização reversa máxima sobre o diodo.

5
EXEMPLO 3.1
6
EXEMPLO 3.1





O diodo conduz quando vs>12, ou seja
24sin()=12
que tem como solução
1=30° e 2=150°
ou seja, conduz durante =2-1=120°, o que
representa 1/3 do período.
A corrente de pico vale
Id=(24-12)/100=0,12 A
A tensão reversa máxima é igual a:
Vd=12-(-24)=36 V
7
EXEMPLO 3.2



Determine V e I no circuito com diodos a seguir.
Na primeira figura, supondo ambos os diodos
conduzindo, temos que:
VB=0, V=0, ID2=1 mA e portanto I=1 mA.
Na segunda figura, supondo ambos os diodos
conduzindo, temos que:
VB=0, V=0, ID2=2 mA e I=-1 mA,
o que indica que D1 está cortado, e portanto I=0.
8
EXEMPLO 3.2
9
EXEMPLO 3.2

Além disso,
ID2=20/15k=1,33 mA
V=VB=-10+10k1,33m=3,3 V
o que confirma o corte de D1.
10
CARACTERÍSTICA ELÉTRICA
DE DIODOS REAIS
11
CARACTERÍSTICA ELÉTRICA
DE DIODOS REAIS

Existem 3 regiões distintas:
– Polarização direta se v>0.
– Polarização reversa se v<0
– Região de ruptura se v<-VZK
12
REGIÃO DE POLARIZAÇÃO
DIRETA

Na região de polarização direta:
i=IS{exp[v/(nVT)]-1}
onde IS é denominada corrente de saturação
(da ordem de 10-15 A para pequenos
diodos), VT é denominada tensão térmica e
1n2 é uma constante de fabricação do
diodo.
13
REGIÃO DE POLARIZAÇÃO
DIRETA
A tensão térmica é dada por:
VT=kT/q
onde k=1,3810-23 J/K, T é a temperatura
em K e q=1,610-19 C é a carga de um
elétron, que à temperatura ambiente vale:
VT25 mV.
 No sentido direto para i>>IS
i=ISexp[v/(nVT)]
ou
v=nVTln(i/IS)

14
REGIÃO DE POLARIZAÇÃO
DIRETA
Para v<0,5 V a corrente é desprezível.
Assim, v=0,5 V é denominada tensão de
corte.
 Por outro lado, a queda de tensão de um
diodo em condução é v0,7 V.
 Como IS e VT variam com a temperatura,
dada uma corrente constante, a tensão
diminui 2 mV para cada °C de aumento da
temperatura.

15
VARIAÇÃO DA TENSÃO
COM A TEMPERATURA
16
REGIÃO DE POLARIZAÇÃO
REVERSA
Neste caso, v<0 e portanto a exponencial
torna-se desprezível perante a unidade, e
assim:
I -IS
 Na verdade a corrente reversa é muito maior
que a corrente de saturação, podendo
alcançar 1 nA, e isto se deve a efeitos de
fuga.

17
REGIÃO DE RUPTURA
Ela ocorre quando a tensão reversa for
maior que a tensão de ruptura.
 Neste caso, a corrente aumenta rapidamente
para um aumento pequeno na tensão. Se não
houver um resistor que limite a corrente, o
diodo se destruirá.
 Observe que nesta região, um diodo pode
funcionar como uma fonte de tensão.

18
ANÁLISE DE CIRCUITO
COM DIODOS
19
ANÁLISE DE CIRCUITO
COM DIODOS
Podemos escrever duas equações:
ID=ISexp(VD/nVT)
e
ID=(VDD-VD)/R
 Supondo que IS e n sejam conhecidos, a
solução deste sistema não-linear de
equações não apresenta forma fechada.
 Solução: cálculo numérico ou análise
gráfica.

20
ANÁLISE GRÁFICA
21
MODELO DE SEGMENTOS
LINEARES
22
MODELO DE SEGMENTOS
LINEARES
Neste caso:
iD=0
para vDVD0
ID=(vD-VD0)/rD para vDVD0
onde para o exemplo anterior
VD0=0,65 V e rD=20 
 O modelo de segmentos lineares pode ser
modelado pelo circuito a seguir.

23
MODELO DE SEGMENTOS
LINEARES
24
EXEMPLO 3.5

Obtenha a corrente e a tensão no diodo para
o circuito com diodo e resistor mostrado
anteriormente utilizando o modelo de
segmentos lineares com
VD0=0,65 V
rD=20 
R=1 k
25
EXEMPLO 3.5
26
EXEMPLO 3.5
Neste caso, podemos escrever para a
corrente no diodo:
ID=(VDD-VD0)/(R+rD)
ID=(5-0,65)/(1000+20)=4,3 mA
 A tensão no diodo é dada por:
VD=VD0+rDID
VD=0,65+204,310-3=0,735 V

27
MODELO DE QUEDA DE
TENSÃO CONSTANTE
28
MODELO DE QUEDA DE
TENSÃO CONSTANTE
Neste caso, podemos escrever que:
ID=(VDD-VD0)/R
onde tipicamente VD0=0,7 V.
 Para o exemplo anterior:
ID=(5-0,7)/1000=4,3 mA

29
MODELO DE QUEDA DE
TENSÃO CONSTANTE
30
MODELO PARA PEQUENOS
SINAIS
Considere um diodo polarizado para operar
com um sinal em torno do ponto quiescente.
 A tensão total no diodo é dada por:
vD(t)=VD+vd(t)
 A corrente instantânea pode ser escrita
como:
iD(t)=ISexp[(VD+vd)/nVT]
iD(t)=ISexp(VD/nVT)exp(vd/nVT)
iD(t)=IDexp(vd/nVT)

31
MODELO PARA PEQUENOS
SINAIS
32
MODELO PARA PEQUENOS
SINAIS

Supondo que vd/nVT<<1, podemos
aproximar a exponencial pelos dois
primeiros termos de sua série de Taylor:
iD(t)=ID(1+vd/nVT)
iD(t)=ID+(ID/nVT)vd
iD(t)=ID+id
onde
id=vd/rd
33
MODELO PARA PEQUENOS
SINAIS
E portanto,
rd=nVT/ID
 Ou seja a resistência dinâmica é
inversamente proporcional à corrente.
 E portanto,
vD(t)=VD+rdid
 De onde, tiramos o modelo circuital a
seguir.

34
MODELO PARA PEQUENOS
SINAIS
35
CIRCUITOS EQUIVALENTES
PARA PEQUENOS SINAIS
36
EXEMPLO 3.6
Considere o circuito a seguir, no qual a
fonte de tensão V+ tem um valor DC de 10
V, sobreposto a uma ondulação senoidal de
60 Hz de 1 V de pico.
 Calcule a amplitude do sinal senoidal sobre
o diodo. Suponha que VD=0,7 V, R=10 k
e n=2.

37
EXEMPLO 3.6
38
EXEMPLO 3.6
Do ponto de vista DC,
ID=(10-0,7)/10=0,93 mA
 A resistência dinâmica é dada por:
rd=nVT/ID=225/0,93=53,8 
 A tensão senoidal sobre o diodo vale:
vd=v+rd/(rd+R)=5,4 mV
e que por ser pequeno (<< 10 mV) justifica
a aplicação do modelo de pequenos sinais.

39
DIODOS ZENER
40
MODELO PARA O DIODO
ZENER

Um diodo zener na região de ruptura pode
ser modelado por:
VZ=VZ0+rzIZ
para IZIZK
onde VZ0 é o ponto em que a curva do zener
intercepta o eixo de tensão, e rz representa a
inclinação daquela curva.
41
MODELO PARA O DIODO
ZENER
42
EXEMPLO 3.8
Seja o circuito da figura a seguir, onde um
diodo zener é utilizado. A tensão de zener
VZ=6,8 V é obtida para uma corrente de
zener IZ=5 mA, com rz=20  e IZK=0,2 mA.
A fonte de alimentação V+=101 V.
 Determine VO sem carga usando V+
nominal.
 Calcule a variação de VO resultante da
variação de 1 V em V+.

43
EXEMPLO 3.8
Calcule a variação em VO resultante da
conexão de uma carga de RL=2 k.
 Calcule a variação em VO quando RL=0,5
k.
 Qual o valor mínimo de RL para o diodo
continuar a operar na região de ruptura.

44
EXEMPLO 3.8
45
EXEMPLO 3.8
Podemos determinar inicialmente,
VZ0=VZ-rzIZ=6,8-20510-3=6,7 V
 Sem carga, temos que
IZ=(V+-VZ0)/(R+rz)=(10-6,7)/520=6,3 mA
 Portanto,
VO=VZ0+IZrz=6,7+6,310-320=6,83 V
 Para uma variação V+=1 V, temos que
VO=V+rz/(rz+R)=120/520=38,5 mV

46
EXEMPLO 3.8
Uma carga de 2 k vai drenar
aproximadamente 3,4 mA, portanto
VO=rzIZ=-203,410-3=-68 mV
 Uma carga de 500  vai drenar
aproximadamente 13,6 mA, o que não é
possível, pois a corrente pelo resistor é de
apenas 6,4 mA. Neste caso o zener estará
cortado e a tensão de saída será dada por
VO=V+RL/(R+RL)=10/2=5 V
o que confirma o corte do zener.

47
EXEMPLO 3.8

Para o zener operar com corrente IZK=0,2
mA, temos que VZ=VZKVZ0=6,7 V. Neste
caso, a corrente de pior caso que passa por
R é (9-6,7)/0,5=4,6 mA, e portanto a
corrente que sobra na carga é 4,6-0,2=4,4
mA. Portanto,
RL=6,7/4,4=1,5 k.
48
PROJETO DE REGULADOR
ZENER
Considere o regulador com zener a seguir.
 O regulador é alimentado com uma tensão
que possui uma grande ondulação.
 A função do regulador é fornecer uma
tensão de saída que seja a mais constante
possível, independente de:

–
–
–
Tensão de Entrada
Variações da carga.
Ondulação da tensão de entrada.
49
PROJETO DE REGULADOR
ZENER
50
PROJETO DE REGULADOR
ZENER

Dois parâmetros são usados para medir a
qualidade de um regulador.
–
–

Regulação de Linha:
RL=VO/VS
Regulação de Carga:
RC=VO/IL
Utilizando a próxima figura, temos para o
regulador zener que:
VO=VZ0R/(R+rz)+VSrz/(R+rz)-ILRrz/(R+rz)
51
PROJETO DE REGULADOR
ZENER
52
PROJETO DE REGULADOR
ZENER
Portanto,
RL=rz/(R+rz)
RC=-Rrz/(R+rz)
 Altos valores de R são desejáveis. No
entanto o valor máximo de R deve satisfazer
R=(VSmin-VZ0-rzIZmin)/(Izmin+ILmax)
pois baixos valores de VS e altos valores de
IL conduzem a baixos valores de IZ.

53
EXEMPLO 3.9
Projete um regulador zener para:
VO=7,5 V
15VS25 V
0IL15 mA
VZ=7,5 V para IZ=20mA e rz=10 .
 Calcule R e determine as regulações de
linha e de carga.

54
EXEMPLO 3.9



Podemos determinar inicialmente,
VZ0=VZ-rzIZ=7,5-102010-3=7,3 V
A seguir, escolhendo que Izmin=5 mA, temos
R=(VSmin-VZ0-rzIZmin)/(Izmin+ILmax)
R=(15-7,3-10510-3)/(2010-3)=383 
Portanto,
RL=rz/(R+rz)=25,4 mV/V
VO=0,25 V
RC=-Rrz/(R+rz)=-9,7 V/A
VO=-0,15 V
55
COEFICIENTE DE
TEMPERATURA DOS ZENERS
Os diodos zener exibem um coeficiente de
temperatura negativo se a sua tensão de
zener for menor que 5 V.
 Por outro lado, diodos com tensão acima de
5 V, apresentam coeficiente de temperatura
positivo.
 A combinação em série de um zener com
um TC de 2 mV/°C e um diodo com TC de
–2 mV/°C proporciona uma tensão de
VZ+VD e que é estável com temperatura.

56
FONTE DE ALIMENTAÇÃO
DC
57
RETIFICADOR DE MEIA
ONDA
Considere o retificador de meia onda a
seguir. A tensão de saída é dada por:
vO=0
para vS<VD0
vO=(vS-VD0)R/(R+rD) para vSVD0
 Se rD<<R então
vOvS-VD0
para vSVD0
 A tensão de pico reversa sobre o diodo é
PIV=Vs

58
RETIFICADOR DE MEIA
ONDA
59
RETIFICADOR DE ONDA
COMPLETA
Considere o retificador de onda completa a
seguir. A tensão de saída é dada por:
vO=(vS-VD0)R/(R+rD)
 Se rD<<R então
vOvS-VD0
 A tensão de pico reversa sobre o diodo é
PIV=2Vs-VD0

60
RETIFICADOR DE ONDA
COMPLETA
61
RETIFICADOR EM PONTE
Considere o retificador em ponte a seguir.
 A tensão de saída é dada por:
vO=(vS-2VD0)R/(R+2rD)
 Se rD<<R então
vOvS-2VD0
 A tensão de pico reversa sobre o diodo é
PIV=Vs-VD0

62
RETIFICADOR EM PONTE
63
RETIFICADOR DE MEIA
ONDA COM FILTRO IDEAL
64
RETIFICADOR DE MEIA
ONDA COM FILTRO REAL


Considere o retificador com filtro a seguir.
Vamos supor que
–
–
–


RC>>T.
O diodo conduz por um breve intervalo de tempo t.
No intervalo de corte, o capacitor C se descarrega
através do resistor R.
No intervalo de corte,
Vo=Vpexp(-t/RC)
Ao final do intervalo de descarga
Vp-VrVpexp(-T/RC)
65
RETIFICADOR DE MEIA
ONDA COM FILTRO
66
RETIFICADOR DE MEIA
ONDA COM FILTRO




Usando a aproximação por série de Taylor que:
exp(-T/RC)=1-T/(RC)
Portanto,
VrVpT/(RC)=Vp/(fRC)
O valor médio da tensão de saída é dada por:
VOVp-Vr/2=Vp[1-1/(2fRC)]
O ângulo de condução do diodo pode ser obtido a
a partir de:
Vpcos(2ft)=Vpcos()=Vp-Vr
67
RETIFICADOR DE MEIA
ONDA COM FILTRO




Usando a aproximação por série de Taylor que:
cos()1-2/2
Portanto, o período de condução do diodo é:
=(2Vr/Vp)=[2/(fRC)]
A carga ganha pelo capacitor no instante t é igual
àquela perdida no intervalo de descarga, ou seja:
iCmedt =CVr
A corrente média que passa pelo capacitor é dada
por:
iCmed=iDmed-iLmediDmed-IL
68
RETIFICADOR DE MEIA
ONDA COM FILTRO





Assim,
iDmed=IL+CVr/t
Substituindo que
2ft=(2Vr/Vp)
E que
Vr=Vp/(fRC)
Portanto,
iDmed=IL[1+(2Vp/Vr)]
Pode-se mostrar que:
iDmax=IL[1+2(2Vp/Vr)]2iDmed
69
RETIFICADOR DE ONDA
COMPLETA COM FILTRO
Para este caso, pode-se mostrar que:
Vr=Vp/(2fRC)
IDmed=IL[1+(Vp/2Vr)]
IDmax=IL[1+2(Vp/2Vr)]2IDmed
 Como conclusão, para uma mesma
ondulação, o capacitor neste caso pode ter a
metade do valor daquele utilizado no
retificador de meia onda. Além disso, a
corrente que passa pelos diodos é a metade
da corrente do caso meia-onda.
70

EXEMPLO 3.10
Considere um retificador de meia onda
com:
f=60 Hz
Vp=100 V
R=10 k
Vr=2 V
 Obtenha C, a fração do ciclo em que o
diodo conduz, o valor médio e o de pico da
corrente que passa pelo diodo.

71
EXEMPLO 3.10




O capacitor pode ser obtido de:
C=Vp/(VrfR)=83,3 F
O ângulo de condução pode ser calculado por:
=(2Vr/Vp)=0,2 rad
A corrente média na carga é dada por:
IL=Vp/R=10 mA
A corrente média e a máx podem ser calculadas
por:
IDmed=IL[1+(2Vp/Vr)]=324 mA
IDmax=IL[1+2(2Vp/Vr)]=638 mA
72
RETIFICADORES IDEAIS
73
CARACTERÍSTICA DE
TRANSFERÊNCIA DE UM LIMITADOR
74
SENÓIDE APLICADA A UM
LIMITADOR
75
CIRCUITOS LIMITADORES
76
CIRCUITO GRAMPEADOR
OU RESTAURADOR DE DC
77
CIRCUITO DOBRADOR DE
TENSÃO
78
JUNÇÃO PN
Um diodo semicondutor é composto da
união de 2 materiais semicondutores:
 silício tipo p
 silício tipo n

79
JUNÇÃO PN
80
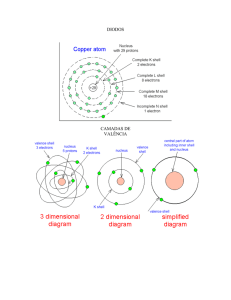
SILÍCIO INTRÍNSECO
Um cristal de silício puro tem uma estrutura
atômica regular em que cada átomo
compartilha os 4 elétrons da banda de
valência.
 As ligações entre os átomos de silício são
denominadas ligações covalentes.
 Na temperatura ambiente, alguns elétrons
conseguem se libertar através da ionização
térmica, incidência de luz, ou campo
elétrico, rompendo a ligação covalente.

81
SILÍCIO INTRÍNSECO
Como resultado, o átomo passa a ter carga
positiva.
 Por sua vez, esta carga positiva pode atrair
outros elétrons livres.
 Esta união preenche a lacuna positiva que
havia no átomo ionizado e é denominada
recombinação.

82
SILÍCIO INTRÍNSECO
Deste modo, temos elétrons e lacunas como
portadores de cargas movendo-se pelo
cristal.
 A lacuna tem carga positiva e valor igual à
do elétron.
 A ionização térmica produz concentrações
iguais de elétrons e lacunas.

83
TAXA DE RECOMBINAÇÃO
E DE IONIZAÇÃO



A taxa de recombinação depende do números de
elétrons e lacunas livres, que por sua vez, depende
da taxa de ionização.
Em equilíbrio térmico a taxa de recombinação é
igual à taxa de ionização.
O número de elétrons e lacunas livres é igual entre
si:
n=p=ni
onde ni representa a concentração para o silício
puro.
84
CONCENTRAÇÃO DE
PORTADORES

Do estudo da física de semicondutores,
mostra-se que:
ni=BT3exp(EG/kT)
onde B depende do material com
B=5,410-31 port/K3/cm3 para o silício, EG é
conhecido como largura de energia da faixa
proibida com EG=1,12 eV para o silício e
k=8,6210-5 eV/K é a constante de
Boltzmann.
85
CONCENTRAÇÃO DE
PORTADORES
À temperatura ambiente T=300 K, temos
que:
ni=1,51010 port/cm3
 A concentração de átomos em um cristal de
silício é de 51022 átomos/cm3.
 Daí se entende perfeitamente porque o
silício puro é um material semicondutor.

86
CORRENTE DE DIFUSÃO E
DE DERIVA

Existem 2 mecanismos de condução de
portadores em um cristal semicondutor:
–
–

difusão
deriva
A difusão ocorre pela concentração nãouniforme de portadores no cristal, como
mostra a figura a seguir.
87
CORRENTE DE DIFUSÃO
88
CORRENTE DE DIFUSÃO



Como os portadores movem-se sempre da maior
concentração para a menor, temos a densidade de
corrente de difusão para as lacunas:
Jp=-qDpp/x
onde Dp é a constante de difusão das lacunas.
E para os elétrons:
Jn=qDn n/x
onde Dn é a constante de difusão dos elétrons.
Para o silício puro Dp=12 cm2/s e Dn=34 cm2/s.
89
VELOCIDADE DE DERIVA


O outro mecanismo de movimento dos portadores
deve-se à ação de um campo elétrico, e é
denominado deriva.
As velocidades de deriva para as lacunas e
elétrons são dadas por:
vderiva,p=pE
vderiva,n=-nE
onde p e n são denominadas mobilidade das
lacunas e elétrons, respectivamente, que para o
silício intrínseco valem p=480 cm2/Vs e n=1350
cm2/Vs.
90
CORRENTE DE DERIVA



As correntes de deriva para as lacunas e elétrons
são dadas por:
Ideriva,p=qp pEA
Ideriva,n=qn nEA
A corrente total é a soma das correntes anteriores,
ou seja:
Ideriva=q(pp+nn)EA
Finalmente, existe a relação de Einstein dada por:
Dp/p=Dn/n=VT
91
SEMICONDUTORES TIPO N
Considere um cristal de silício intrínseco
dopado com um elemento pentavalente,
como o fósforo.
 Ao se ligar com o silício da rede cristalina,
o fósforo doa um elétron livre.
 As impurezas de fósforo são denominadas
doadoras.
 A dopagem de um cristal intrínseco com o
fósforo forma um silício do tipo n.

92
SEMICONDUTORES TIPO N
Se a densidade de átomos doadores for ND,
então a densidade de elétrons livres em um
silício tipo n é dada por:
nn0ND
 Da física de semicondutores, em equilíbrio
térmico:
nn0pn0=ni2
ou seja a densidade de lacunas diminui, por
conta da densidade de elétrons ter sido
aumentada.

93
SEMICONDUTORES TIPO P




Considere um cristal de silício intrínseco
dopado com um elemento trivalente, como o
boro.
Ao se ligar com o silício da rede cristalina, o
boro dá origem a uma lacuna, ou seja aceita
um elétron livre.
As impurezas de boro são denominadas
aceitadoras.
A dopagem de um cristal intrínseco com o
boro forma um silício tipo p.
94
SEMICONDUTORES TIPO P
Se a densidade de átomos aceitadores for
NA, então a densidade de lacunas livres em
um silício tipo p é dada por:
pp0NA
 Da física de semicondutores, em equilíbrio
térmico:
np0pp0=ni2
ou seja a densidade de elétrons diminui, por
conta da densidade de lacunas ter sido
aumentada.
95

JUNÇÃO PN EM ABERTO




Considere uma junção pn em aberto,
Pelo fato de a concentração de elétrons ser
grande na região n e baixa na região p, existe
uma difusão de elétrons através da junção para o
lado p.
Do mesmo modo, existe uma difusão de lacunas
para o lado n.
Esta difusão de portadores deixa a descoberto
cargas fixas positivas no lado n e negativas no
lado p.
96
JUNÇÃO PN EM ABERTO
97
REGIÃO DE DEPLEÇÃO
Esta região livre de portadores é
denominada região de depleção.
 A região de depleção dá origem a um
campo elétrico que tende a se opor à
passagem dos portadores através da junção.
 Por outro lado, elétrons e lacunas
minoritárias gerados termicamente na
região de depleção dos lados p e n,
respectivamente, atravessam a junção.

98
TENSÃO INTERNA DE UMA
JUNÇÃO PN
No equilíbrio,
ID=IS
ou seja, a corrente de difusão é igual à de
deriva.
 Pode-se mostrar que a tensão desenvolvida
em uma junção pn é dada por:
V0=VTln(NAND/ni2)
onde 0,6V00,8 V é também denominado
potencial de contacto.

99
LARGURA DA REGIÃO DE
DEPLEÇÃO
A largura da região de depleção, tanto no
lado p, quanto n, depende da carga em cada
lado, ou seja:
qxpNAA=qxnNDA
 Que pode ser simplificada para
xpNA=xnND
 Da física de dispositivos:
Wdep=xn+xp=[2(1/NA+1/ND)V0/q]
onde =1,0410-12 F/cm é a permissividade
100
do silício.

JUNÇÃO PN REVERSAMENTE
POLARIZADA
Colocando-se uma tensão reversa VR entre
os terminais do diodo, temos que a região
de depleção aumenta, pois mais lacunas do
lado p serão repelidas pelo positivo da
bateria, e vice-versa.
 A corrente de difusão ID diminui, como
conseqüência do aumento da tensão na
região de depleção.

101
JUNÇÃO PN REVERSAMENTE
POLARIZADA
102
JUNÇÃO PN REVERSAMENTE
POLARIZADA

Além disso, a corrente de deriva é
independente da tensão de barreira.
 Portanto,
I=IS-IDIS
a corrente em uma junção reversamente
polarizada é devido a portadores gerados
por ionização térmica, que é bastante
pequena.
103
CAPACITÂNCIA DE
DEPLEÇÃO
A região de depleção forma uma
capacitância.
 A carga armazenada já foi deduzida
anteriormente,
qJ=qN=qNDxnA
 Além disso, de equações anteriores,
podemos escrever que:
xn=WdepNA/(NA+ND)

104
CAPACITÂNCIA DE
DEPLEÇÃO
Portanto,
qJ=qNANDAWdep/(NA+ND)
onde
Wdep=[(2/q)(1/NA+1/ND)(V0+VR)]
 A carga pode ser reescrita como:
qJ=[2qNANDA2(V0+VR)/(NA+ND)]
 A relação entre qj e VR não é linear. Do
ponto de vista de pequenos sinais,
Cj=qj/VR

105
CAPACITÂNCIA DE
DEPLEÇÃO
106
CAPACITÂNCIA DE
DEPLEÇÃO

E portanto
Cj=Cj0/(1+VR/V0)
onde
Cj0=[(q/2)A2NAND/(NA+ND)/V0]
107
JUNÇÃO PN NA REGIÃO DE
RUPTURA
Considere uma junção pn excitada com uma
fonte de corrente I>IS, conforme a figura a
seguir.
 Existem 2 mecanismos possíveis de ruptura:

–
–
Efeito zener: ocorre ruptura para VR<5 V.
Efeito de avalanche: ocorre ruptura para VR>7
V.
108
JUNÇÃO PN NA REGIÃO DE
RUPTURA
109
EFEITO ZENER E DE
AVALANCHE
A ruptura zener ocorre quando o campo
elétrico é capaz de quebrar uma ligação
covalente.
 A ruptura por avalanche ocorre quando os
portadores minoritários ganham do campo
elétrico energia cinética suficiente para
quebrar ligações covalentes. Os portadores
liberados por este processo produzem outras
colisões ionizantes.

110
JUNÇÃO PN COM
POLARIZAÇÃO DIRETA



Considere uma junção PN polarizada
diretamente com uma fonte de tensão externa.
A fonte externa consegue neutralizar a barreira
de potencial proporcionada pelas cargas fixas,
que além de diminuir a região de depleção, faz
com que portadores majoritários consigam
passar pela junção.
Os portadores majoritários tornam-se
minoritários ao chegar ao outro lado da junção.
111
JUNÇÃO PN COM
POLARIZAÇÃO DIRETA
112
DISTRIBUIÇÃO DE PORTADORES
MINORITÁRIOS
A figura a seguir ilustra a distribuição de
portadores minoritários.
 A distribuição de lacunas no lado n é grande
próxima da junção e vai diminuindo devido
à recombinação com os elétrons, e é dada
por um perfil exponencial negativo:
pn(x)=pn0+[pn(xn)-pn0]exp[-(x-xn)/Lp]
onde 1Lp 100 m é denominado
comprimento de difusão.

113
DISTRIBUIÇÃO DE PORTADORES
MINORITÁRIOS
114
JUNÇÃO PN COM
POLARIZAÇÃO DIRETA


Além disso,
Lp=(Dpp)
onde 1p10.000 ns é o tempo de vida das
lacunas.
Da física de semicondutores temos a lei da
junção, que diz que a concentração próxima da
junção é muito maior que longe da junção:
pn(xn)=pn0exp(V/VT)
115
JUNÇÃO PN COM
POLARIZAÇÃO DIRETA


A corrente de difusão, devido ao perfil pn(x):
Ip=-qADpp/x
Ip=(qADppn0/Lp)[exp(V/VT)-1]
exp[-(x-xn)/Lp]/Lp
A corrente no lado n é constante, pois existe a
corrente devido aos elétrons. A corrente na
borda da região de depleção vale:
Ip=qADppn0[exp(V/VT)-1]/Lp
In=qADnnp0[exp(V/VT)-1]/Ln
116
JUNÇÃO PN COM
POLARIZAÇÃO DIRETA
A corrente total é dada por:
I=qA(Dppn0/Lp+Dnnp0/Ln)[exp(V/VT)-1]
 Usando que pn0=ni2/ND e np0=ni2/NA, temos:
I=IS[exp(V/VT)-1]
onde
IS=qAni2[Dp/(NDLp)+Dn/(NALn)]

117
CAPACITÂNCIA DE
DIFUSÃO
Existe um excesso de cargas que precisa ser
eliminada, em caso de mudança de tensão:
Qp=Aqxn[pn(x)-pn0]dx
Qp=AqLp[pn(xn)-pn0]
 Substituindo que pn(xn)=pn0exp(V/VT) e que
Ip=qADppn0[exp(V/VT)-1]/Lp, temos que:
Qp=Lp2Ip/Dp
ou ainda
Qp=pIp

118
CAPACITÂNCIA DE
DIFUSÃO



A carga total é dada por:
Q=pIp+nIn
Esta carga pode ser escrita em termos da corrente
total:
Q=TI
onde T é denominado tempo médio de trânsito.
Para pequenos sinais:
Cd=Q/V
Cd=(T/VT)I
119
CAPACITÂNCIA DE
DEPLEÇÃO

Para polarização direta, usa-se a seguinte
regra prática:
Cj2Cj0
120
MODELO DE DIODO PARA
ALTAS FREQÜÊNCIAS

No modelo de um diodo para pequenos
sinais e altas freqüências deve se incluir as
capacitâncias de depleção e de difusão,
onde:
Cd=(T/VT)ID
Cj=Cj0/(1+VD/V0)m
para VD<0
Cj2Cj0
para VD>0
121
MODELO DE DIODO PARA
ALTAS FREQÜÊNCIAS
122
DIODOS ESPECIAIS
Diodo Schottky: é formado pela junção de
um metal (anodo) com um semicondutor
tipo n. Como característica exibem tensão
de condução de 0,3 V. São muito rápidos
em utilizados em chaveamento.
 Varactores ou Diodos Capacitivos:
Dispositivos que trabalham reversamente
polarizados e que são otimizados para
apresentar uma grande variação de
capacitância em função da tensão.

123
DIODOS ESPECIAIS


Fotodiodos: Trabalham reversamente
polarizados. A incidência de fótons em uma
junção PN produz um par elétron-lacuna na
região de depleção, responsável pela
fotocorrente.
Diodos Emissores de Luz (LEDs): Realiza a
função inversa dos fotodiodos. Trabalha
diretamente polarizado. Portadores
minoritários em difusão podem se recombinar
com portadores majoritários o que pode
produzir um fóton em materiais como o
124
arseneto de gálio.