DIFERENÇAS DE POTENCIAL NUM CAMPO ELÉCTRICO

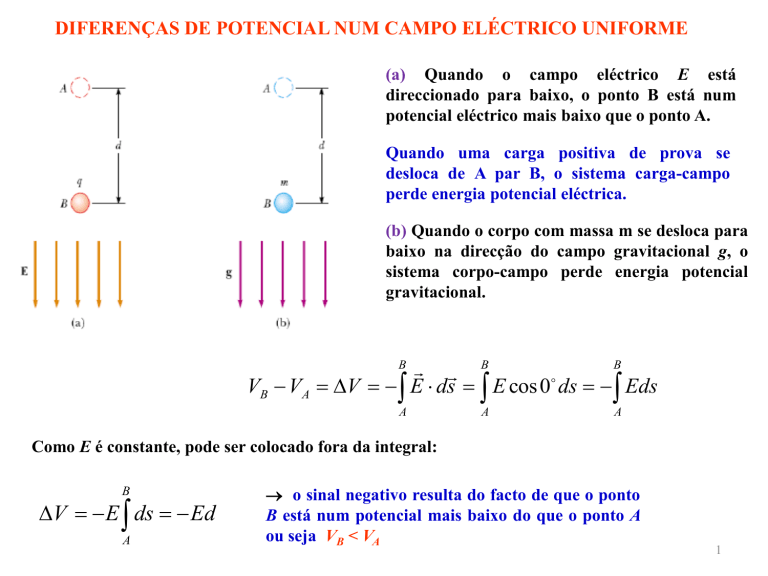
DIFERENÇAS DE POTENCIAL NUM CAMPO ELÉCTRICO UNIFORME
(a) Quando o campo eléctrico E está
direccionado para baixo, o ponto B está num
potencial eléctrico mais baixo que o ponto A.
Quando uma carga positiva de prova se
desloca de A par B, o sistema carga-campo
perde energia potencial eléctrica.
(b) Quando o corpo com massa m se desloca para
baixo na direcção do campo gravitacional g, o
sistema corpo-campo perde energia potencial
gravitacional.
B
  B

VB  VA  V    E  ds   E cos 0 ds    Eds
B
A
A
A
Como E é constante, pode ser colocado fora da integral:
B
V   E  ds   Ed
A
 o sinal negativo resulta do facto de que o ponto
B está num potencial mais baixo do que o ponto A
ou seja VB < VA
1
Quando a carga de prova q0 se desloca de A para B
A variação da energia potencial eléctrica do sistema
campo – carga é
U  q0 V  q0 Ed
Por esse resultado, vemos que se q0 for positiva, então
U é negativa
Se q0 for negativa, então U na equação acima é
positiva e a situação está invertida.
O sistema campo - carga perde energia potencial
eléctrica quando uma carga negativa se desloca na
direcção oposta à do campo eléctrico.
Não temos nenhum análogo para essa
situação no caso gravitacional porque
nenhuma massa negativa foi observada
até o momento.
2
Exemplo
O sistema campo - carga perde energia
potencial eléctrica quando uma carga
positiva se desloca na direcção do campo
eléctrico.
O sistema campo - carga perde energia
potencial eléctrica quando uma carga
negativa se desloca na direcção oposta à
do campo eléctrico.
3
Considere agora o caso mais geral de uma partícula carregada que se desloca entre dois
pontos quaisquer num campo eléctrico uniforme
 
 B 
 
V    E  ds   E   ds  E  r
B

r
A
A
representa o vector deslocamento entre os
pontos A e B

r
A variação na energia potencial eléctrica do
sistema campo - carga é
 
U  q0 V  q0 E  r
Os nossos resultados mostram que todos os pontos num plano perpendicular a um campo eléctrico
uniforme estão no mesmo potencial
Da figura, obtemos:
 
VB - VA =  E  r   Er cos = - Ed = VC - VA
 VB = VC
4
O nome superfície equipotencial é dado a toda superfície que consista numa distribuição
contínua de pontos que têm o mesmo potencial eléctrico.
Observe que, como U  q0 V , nenhum trabalho é necessário para mover uma partícula de
prova entre dois pontos quaisquer e numa superfície equipotencial.
U  WE  K
As superfícies equipotenciais dum campo eléctrico uniforme consistem numa família de planos,
todos perpendiculares ao campo.
Exemplos: Quatro superfícies equipotenciais.
O campo eléctrico é perpendicular às superfícies
Trabalho realizado pelo campo eléctrico
sobre uma partícula carregada quando se
move de um extremo a outro.
5
EXEMPLO
Num campo elétrico, transporta-se uma carga q de 2 µC de ponto X até um ponto Y.
O trabalho da força elétrica é de -0,6 µJ. Determine a ddp entre os pontos X e Y.
WE  0.6 μJ

q  2 C
U  WE  K
Y
V 
U

q
0.6 10 6
V 
 0.3 V
6
2 10
X
6
POTENCIAL ELÉCTRICO DEVIDO À CARGAS PONTUAIS
Vamos agora focalizar nossa atenção nas cargas pontuais, que sabemos que produzem campos
eléctricos que não são uniformes.
Considere uma carga pontual positiva isolada q
 
VB  V A    E  ds
B
mas
A
 
q  
E  ds  k e 2 rˆ  ds
r
onde
 
rˆ  ds  ds cos  dr
Substituindo na integral fica
rB
rB
rB
 
q
dr k q 
VB  VA    E  ds    ke 2 dr  ke q  2  e 
r
r
r  rA
A
rA
rA
B
1 1
 ke q  
 rB rA 
Os dois círculos tracejados representam
secções transversais das superfícies
equipotenciais esféricas
 esta equação expressa o importante
resultado de que a diferença de
potencial entre quaisquer dois pontos
A e B depende somente das
coordenadas radiais rA e rB
7
Como já vimos pode-se definir o potencial de referência como sendo zero em rA = 
Com essa escolha, o potencial eléctrico
devido a uma carga pontual a qualquer
distância r da carga é
q
q
V  ke
r
V é constante sobre uma superfície esférica de raio r centrado na carga pontual
O potencial eléctrico de duas ou mais cargas pontuais é obtido aplicando-se o princípio da
sobreposição
Para um conjunto de cargas, podemos escrever o potencial total em P na forma
qi
V   ke
ri
i
Observe que a soma nessa equação é uma soma algébrica de grandezas escalares em vez de uma
soma vectorial (que é utilizada para calcular o campo eléctrico de um conjunto de cargas)
Além disso é muito mais fácil calcular V para muitas cargas do que calcular o campo eléctrico
8
ENERGIA POTENCIAL ELÉCTRICA DEVIDO À CARGAS PONTUAIS
Energia potencial eléctrica de interacção de um sistema de partículas carregadas
Se V2 for o potencial eléctrico no ponto P devido à carga q2, o trabalho (de um agente externo) necessário para
trazer uma segunda carga q1 do infinito ao ponto P será
W  q1V2
esse trabalho representa uma transferência de energia para o
sistema na forma de energia potencial U
U  q1V2  k e
r1 2
q1
r2 3
r1 3
r1 2
q2
r
P
q2
q1 q2
r12
q1
Se tivermos três cargas:
q2
V2  k e
q3
qq
qq
qq
U  ke 1 2  ke 1 3  ke 2 3
r12
r13
r23
q2
r1 2
P
9
OBTENÇÃO DO CAMPO ELÉCTRICO PELO POTENCIAL ELÉCTRICO
B
 
V    E  ds  V    dV
B
A
A
Portanto podemos escrever que a diferença de potencial dV entre dois pontos que distam ds um
do outro como sendo
Para
 
E  Ex
temos que
 
E  ds  Ex dx
ou
 
dV   E  ds

dV   Ex dx
dV
Ex  
dx
 o campo eléctrico é igual a menos derivada do potencial eléctrico com respeito a alguma
coordenada
10
A variação no potencial é nula para qualquer deslocamento perpendicular ao campo eléctrico
Isso é consistente com a noção de que as superfícies equipotenciais são perpendiculares ao campo:
Campo eléctrico uniforme
Dipolo eléctrico
Carga pontual
Distribuição de carga tem simetria esférica

 
dV
Er  
dV   E  ds   E
r dr
dr
Em geral, o potencial eléctrico é uma função de todas as três coordenadas espaciais  V ( x, y, z )
Ex  
dV
dx
Ey  
é uma equação diferencial, onde
dV
dy
(
Ez  
dV
dz
 
 
 
ex  e y  ez )
x
y
z
e

E  V

o
operador
gradiente
11
POTENCIAL ELÉCTRICO DEVIDO A DISTRIBUIÇÕES CONTÍNUAS DE CARGA
Potencial dV em qualquer ponto P devido ao elemento de carga dq é
dq
dV  k e
r
O potencial total será
V  ke 
dq
r
Um outro método para calcular o potencial de uma distribuição
contínua de carga é utilizar
B 

U
V 
   E  ds
q0
A
Esse procedimento é útil para quando o campo eléctrico já é conhecido a partir de outras
considerações, tais como a lei de Gauss.
Substituímos E e escolhemos, V como zero em algum ponto conveniente.
12
Exemplo: Calcular o potencial no ponto P de um eixo perpendicular ao centro no centro
de um anel de raio a e carga Q
dq
V  ke 

r
como
r  x2  a2
dq
V  ke 
V 
x2  a2
ke
x a
2
2
 dq
 V
keQ
x2  a2
13
POTENCIAL ELÉCTRICO DUM CONDUTOR CARREGADO
Considere um condutor de formato arbitrário com um excesso de carga positiva
A densidade superficial de carga não é uniforme
O condutor está em equilíbrio electrostático 
- toda a carga permanece na superfície, e E = 0 dentro do
condutor
- o campo eléctrico na face externa do condutor é perpendicular à
superfície
Demonstraremos que todo ponto na superfície de um condutor
carregado em equilíbrio electrostático está no mesmo potencial
eléctrico
E é sempre perpendicular ao deslocamento ds entre dois pontos
da superfície. Então
 
E  ds  Eds cos 90   0
 
V  VB  V A    E  ds  0
B
A

 como o campo eléctrico é zero dentro do condutor,
concluímos que o potencial é constante em todo lugar
dentro do condutor e igual a seu valor na superfície.
14
DIFERENÇA DE POTENCIAL E POTENCIAL
RESUMO
Definição de diferença de potencial
B 

U
V 
   E  ds
q0
A
V  VB  VA
 
VP    E  ds
P
Definição de potencial
VA  0
no 

Diferença de potencial e (ou) potencial:
Num campo eléctrico Uniforme 
Devido à uma carga pontual 
V  Ed
1 1
V  ke q   
 rB rA 
Devido à um conjunto de cargas pontuais 
ou
V   ke
i
V  ke
q
r
para A no 
para A no 
qi
ri
Devido à uma distribuição contínua de cargas cargas pontuais  dV  k e
dq
r
 V  ke 
dq
r
 
Potencial eléctrico dum condutor carregado: V  VB  VA    E  ds  0  VB  VA
B
A
 porque no volume, E=0 e na superfície E é perpendicular à trajectória ds
15
Exemplo: Considere uma esfera metálica maciça de raio R e carga total positiva Q.
Como temos um condutor esférico a
distribuição de carga é uniforme
V  ke
Q
r
E  ke
Q
r2
 Potencial fora da esfera
 Campo eléctrico fora da esfera
16
Para determinar como a carga se distribui num condutor não esférico, vamos analisar
um sistema simples
O sistema consiste em duas esferas condutoras carregadas de raio r1 e r2, onde r1 > r2, ligadas por
um fino fio condutor
Supomos que as duas esferas são tão separadas que o campo
eléctrico duma esfera não influencia o campo eléctrico da outra
esfera.
Como as duas esferas são ligadas por um fio condutor  supomos
que todo o sistema é um único condutor e que todos os pontos devem
estar no mesmo potencial
q1
q2
V  ke
 ke
r1
r2


q1 r1

q2 r2
que esfera maior tem a maior quantidade de carga.
Campo eléctrico em cada condutor
q
E1  k e 12
r1
q2
E2  k e 2
r2
17
q1
E1
r12
q1 r22 r1 r22



q2 q2 r12 r2 r12
E2
ke 2
r2
ke

E1 r2

E2 r1
 quer dizer que o campo eléctrico próximo à
esfera menor é maior que o campo próximo à
esfera maior.
 Como o campo eléctrico próximo à superfície de um condutor é proporcional à densidade
superficial de carga, a esfera menor tem a maior densidade superficial de carga.
Esta é a quarta propriedade listada para os condutores em equilíbrio electrostático:
• NUM CONDUTOR DE FORMA IRREGULAR, A CARGA POR UNIDADE DE ÁREA É MÁXIMA NOS
LOCAIS ONDE É MÍNIMO O RAIO DE CURVATURA DA SUPERFÍCIE
Campo forte
Maior densidade superficial de carga
Campo fraco
Menor densidade superficial de carga
18
Exemplo: Duas esferas condutoras. A esfera menor tem raio a e carga Q positiva , e a
esfera maior de raio c não está carregada (neutra).
Ao aproximarmos as duas esferas:
- A esfera menor atrai as cargas negativas da
esfera maior e repele as cargas positivas.
As curvas pontilhadas azuis correspondem as
intersecções das superfícies equipotenciais
com a página.
Como varia o potencial a partir o
centro da esfera 1 até para a
direita da esfera 2, considerando
que b é a distância entre a
superfície da esfera menor e o
centro da esfera maior ?
19
Uma cavidade dentro de um condutor em equilíbrio
Considere um condutor de formato arbitrário contendo uma cavidade.
Se não há cargas dentro da cavidade, o campo
eléctrico dentro da cavidade tem de ser zero,
independentemente da carga na superfície externa do
condutor.
Todo ponto no condutor está no mesmo potencial 
quaisquer dois pontos A e B na superfície da cavidade
têm de estar no mesmo potencial
assim
 
V  VB  V A    E  ds  0
VB  VA  0
B
Por isso E deve ser zero.
A
Esta propriedade pode ser utilizada para blindar um equipamento electrónico ou
até mesmo todo um laboratório dos campos externos cercando-o com paredes
condutores.
20
Exemplo : Blindagem electrostática
No século XIX, por Michael Faraday, através da
seguinte experiência: Electrizou uma grande gaiola
metálica, até que ela soltasse faíscas. Utilizando um
electroscópio, verificou que:
1º O interior da gaiola não ficou electrizado.
2º As cargas em excesso foram tão distanciadas umas
das outras que se concentraram na superfície da
gaiola.
Pêndulo electrostático
Esfera de cortiça pendurada num
fio de seda a esfera não foi atraída
pela parte interna da gaiola só
pela parte externa.
21
A blindagem electrostática mostra que uma pessoa dentro de um carro atingido
por um raio nada sofrerá, pois a estrutura metálica do carro isola o seu interior
das influencias eléctricas externas.
22
COMPARAÇÃO ENTRE O CAMPO ELÉCTRICO E O CAMPO GRAVITACIONAL
Campo Eléctrico
Campo (unidade)
E 
F
q
(N C-1)
q1q2
r2
Força
F  ke
Campo no exterior duma
esfera isolada
Q
E  ke 2
r
Potential no exterior
duma esfera isolada
Energia transferida
V  ke
Q
r
W=qV
Campo gravitacional
g
F
m
F  G
(N kg-1)
m1m2
r2
M
r2
M
V  G
r
g  G
W=mV
23