1ª PROVA DE ELETROMECÂNICA

LISTA 1 DE EXERCÍCIOS DE ANÁLISE DE CIRCUITOS 2
Respostas em vermelho.
1) Para as funções senoidais abaixo, indique a fase, a amplitude, a freqüência angular e o argumento:
a) v (t) = 5cos(200t+10) (V)
Fase: θ=10º / Amplitude=5(V) / Frequência angular=ω=200(rad/s) /
Argumento=ωt=377(rad/s)
b) v (t) = 127cos(377t) (V)
Fase: θ=0º / Amplitude=127(V) / Frequência angular=ω=377(rad/s) /
Argumento=ωt=377t(rad/s)
c) v (t) = 100cos(50t+78) (V)
Fase: θ=78º / Amplitude=100(V) / Frequência angular=ω=50(rad/s) /
Argumento=ωt=50t(rad/s)
d) v (t) = 9cos(377t-35) (V)
Fase: θ=-35º / Amplitude=9(V) / Frequência angular=ω=377(rad/s) /
Argumento=ωt=377t(rad/s)
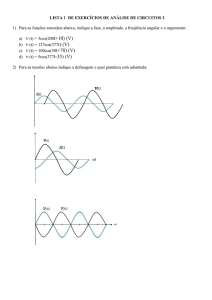
2) Para as tensões abaixo indique a defasagem e qual grandeza está adiantada:
V(t)
i(t)
Defasagem: θ= - 90º
i(t) está adiantada em 90º em relação
a v(t).
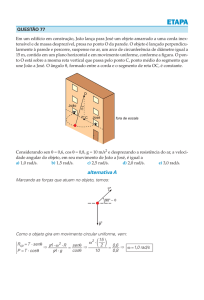
V(t)
i(t)
t
Defasagem: θ= 90º
i(t) está atrasada em 90º em relação a
v(t).
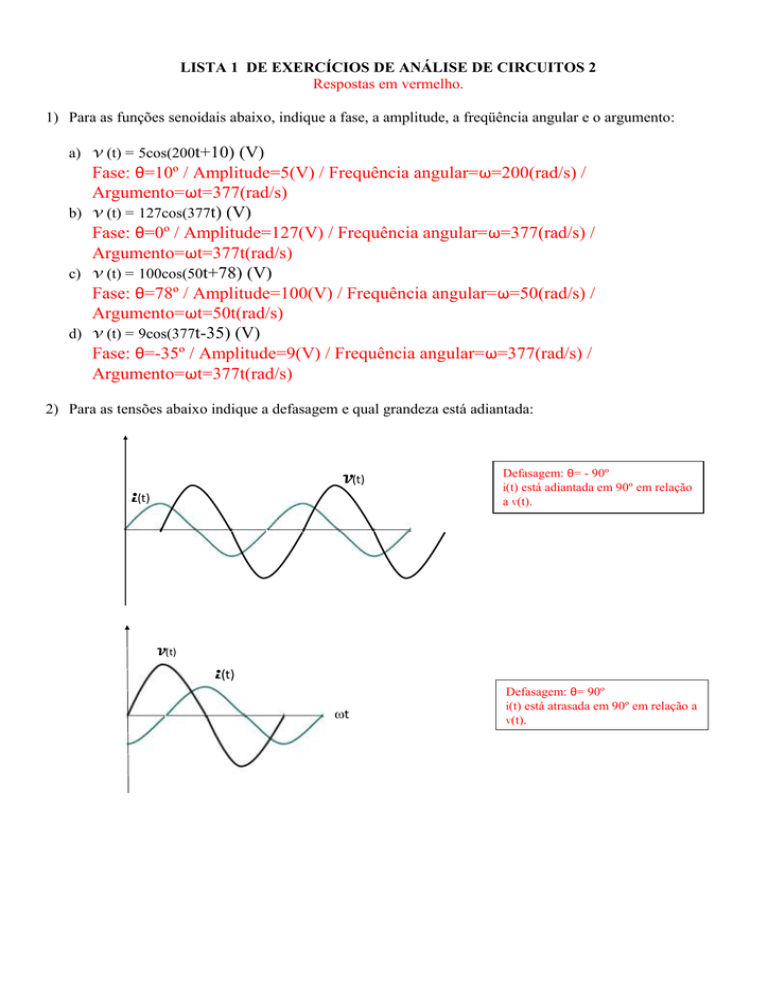
V1(t)
V2(t)
Defasagem: θ=180º
i(t) e v(t) estão em oposição de fase .
t
3) Escreva as tensões e correntes abaixo em notação fasorial (domínio da frequência):
a) v (t) = 5cos(200t-10) (V)
V = 5-10°
b) v (t) = 127cos(377t) (V)
V = 1270°
c) v (t) = 100cos(50t+78) (V)
V = 10078°
d) i (t) = 9cos(377t+35) (A)
V = 935°
e) i (t) = 2cos(377t-250) (A)
V = 2250°
f) i (t) = 300cos(200t+0) (A)
V = 3000°
4) Escreva as tensões e correntes abaixo no domínio do tempo:
a) I = 5-40º (A)
i (t) = 5cos(ωt-40°) (A)
b) v (t) = 1270º (V)
v (t) = 127cos(ωt+0°) (V)
c) v (t) = 100120º (V)
v (t) = 100cos(ωt+120°) (V)
d) v (t) = 9-10º (A)
v (t) = 9cos(ωt-10°) (V)
e) I (t) = 2 35º (A)
i (t) = 2cos(ωt+35°)
f) I (t) = 30090º (A)
i (t) = 300cos(ωt+90°) (A)
OBS.: Com não foi fornecida a freqüência, o argumento é ωt.
5) Se uma fonte de tensão alternada V=38058° (V) alimenta uma carga com L=75 (mH) e R=25 (Ω):
a) Determine a reatância da carga;
XL = 28,27 (Ω)
b) Determine parte real da carga
R = 25 (Ω)
c) Determine impedância da carga;
Z = 25+j28,27 (Ω) = 37,7448,51° (Ω)
d) Determine a corrente do circuito;
I = 10,079,49° (A)
e) Determine o ângulo de fator de potência da carga
 = θZ = 48,51°
6) Se uma fonte de tensão alternada V=38058° (V) alimenta uma carga com C=35 (F) e R=25 (Ω):
a) Determine a reatância da carga;
XC = -75,79 (Ω)
b) Determine parte real da carga
R = 25 (Ω)
c) Determine impedância da carga;
Z = 25-j75,79 (Ω) = 79,81-71,74 (Ω)
d) Determine a corrente do circuito;
I = 4,76129,74° (A)
e) Determine o ângulo de fator de potência da carga
 = θZ = -71,74°
7) Para o circuito abaixo:
a) Qual o valor da capacitância que anula o efeito da indutância?
C = 46,91 (F)
b) Para o item (a), qual o valor da corrente?
I = 6,670° (A)
c) No caso (a), como a fonte de tensão “vê“ o circuito?
A fonte “vê” o circuito como puramente resistivo.
d) Neste caso, há defasagem entre a tensão de alimentação e a corrente? Por que?
Não, porque só há a influência do resistor, ou seja, =0°.
8) Para o circuito da questão (7), ainda:
a) Qual o valor da capacitância para que o ângulo de defasagem entre a tensão da fonte e a corrente seja
de -65° ?
C = 29,92 (F)
b) No item (a) qual dos componentes armazenadores de energia tem maior influência?
A maior influência é capacitiva (θZ negativo = -65°), em relação à influência do indutor.
c) Qual o valor da capacitância para que o ângulo de defasagem entre a tensão da fonte e a corrente seja
de +65° ?
C = 108,49 (F)
d) No item (c) qual dos componentes armazenadores de energia tem maior influência?
O Indutor tem maior influência em relação à influência do capacitor.
 Calculadora traçadora de gráficos trigonométricos: http://web2.0calc.es/
 Aula nºs complexos YouTube com Romulo de Oliveira Albuquerque – Editora Érica:
https://www.youtube.com/watch?v=5xC_CIBlafY