1-) Algumas propriedades dos materiais

1-) Algumas propriedades dos materiais
Resiliência é a propriedade de um corpo de devolver a energia armazenada devido a uma determinada
deformação.
Na página Resistência dos materiais I foi visto que a energia da deformação de uma barra, da condição livre até
a situação de equilíbrio com uma força F, é dada por
W = F2 L / (2 E S). Multiplicando dividendo e divisor por S, temos: W = (F/S)2 L S / 2 E. Lembrando que F/S é
a tensão de deformação σ e L S, o volume da barra: W = σ2 V / 2 E.
Na mesma página pode ser visto pela igualdade #III.4# que a relação entre tensão e deformação é σ = E ε ou E
= σ / ε. Substituindo na igualdade anterior, W = σ ε V / 2.
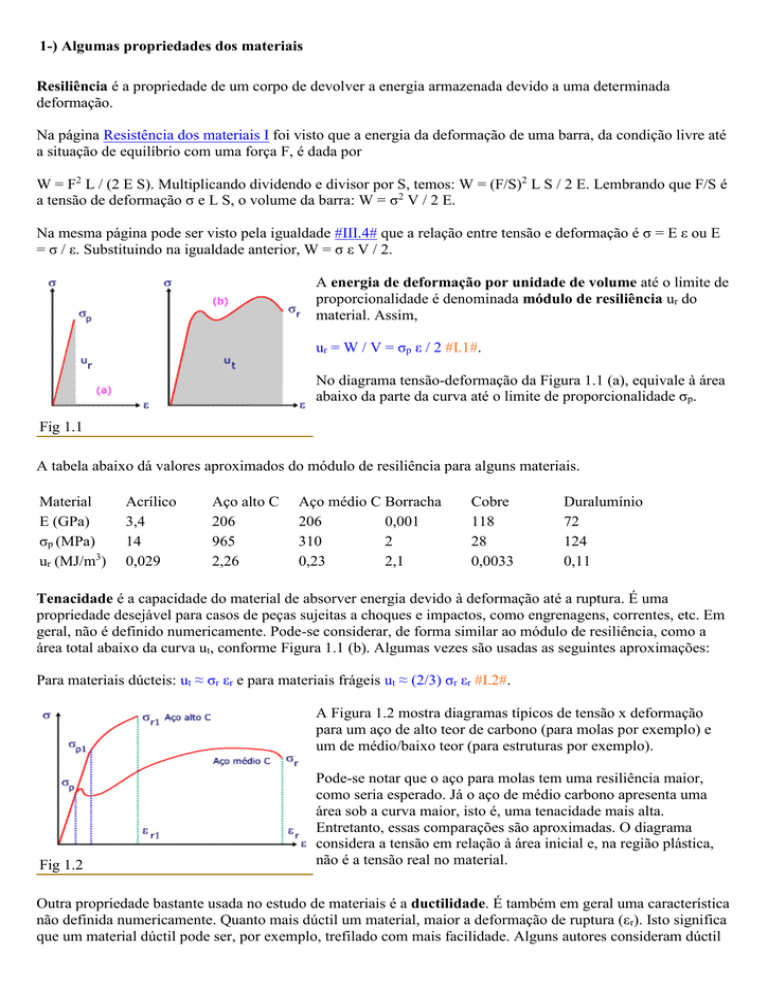
A energia de deformação por unidade de volume até o limite de
proporcionalidade é denominada módulo de resiliência ur do
material. Assim,
ur = W / V = σp ε / 2 #I.1#.
No diagrama tensão-deformação da Figura 1.1 (a), equivale à área
abaixo da parte da curva até o limite de proporcionalidade σp.
Fig 1.1
A tabela abaixo dá valores aproximados do módulo de resiliência para alguns materiais.
Material
E (GPa)
σp (MPa)
ur (MJ/m3)
Acrílico
3,4
14
0,029
Aço alto C
206
965
2,26
Aço médio C Borracha
206
0,001
310
2
0,23
2,1
Cobre
118
28
0,0033
Duralumínio
72
124
0,11
Tenacidade é a capacidade do material de absorver energia devido à deformação até a ruptura. É uma
propriedade desejável para casos de peças sujeitas a choques e impactos, como engrenagens, correntes, etc. Em
geral, não é definido numericamente. Pode-se considerar, de forma similar ao módulo de resiliência, como a
área total abaixo da curva ut, conforme Figura 1.1 (b). Algumas vezes são usadas as seguintes aproximações:
Para materiais dúcteis: ut ≈ σr εr e para materiais frágeis ut ≈ (2/3) σr εr #I.2#.
A Figura 1.2 mostra diagramas típicos de tensão x deformação
para um aço de alto teor de carbono (para molas por exemplo) e
um de médio/baixo teor (para estruturas por exemplo).
Fig 1.2
Pode-se notar que o aço para molas tem uma resiliência maior,
como seria esperado. Já o aço de médio carbono apresenta uma
área sob a curva maior, isto é, uma tenacidade mais alta.
Entretanto, essas comparações são aproximadas. O diagrama
considera a tensão em relação à área inicial e, na região plástica,
não é a tensão real no material.
Outra propriedade bastante usada no estudo de materiais é a ductilidade. É também em geral uma característica
não definida numericamente. Quanto mais dúctil um material, maior a deformação de ruptura (εr). Isto significa
que um material dúctil pode ser, por exemplo, trefilado com mais facilidade. Alguns autores consideram dúctil
o material com deformação de ruptura acima de 0,05. O contrário da ductilidade é a fragilidade. Voltando à
Figura 1.2, podemos notar que aços de elevado carbono são mais frágeis (ou menos dúcteis) que os de médio
carbono.
2-) Tensão admissível e coeficiente de segurança
Os gráficos da Figura 2.1 já foram dados na página Resistência dos materiais I. São curvas típicas aproximadas
de tensão x deformação de materiais dúcteis (a) e frágeis (b). A Figura 1.2 do tópico anterior também mostra a
diferença.
Os materiais frágeis não apresentam limite definido (σe) para as regiões elástica e plástica. Assim, para efeito
de dimensionamento, usa-se a tensão de ruptura (σr). Para os materiais dúcteis, usa-se a tensão de escoamento
σe.
Coeficientes de segurança são usados para prevenir incertezas quanto a propriedades dos materiais, esforços
aplicados, variações, etc.
No caso de peças tracionadas, é usual o conceito da tensão
admissível dada por:
σadm = σe / c para materiais dúcteis.
σadm = σr / c para materiais frágeis.
Onde c é o coeficiente de segurança.
Fig 2.1
A escolha do coeficiente de segurança é uma tarefa de responsabilidade. Valores muito altos significam em
geral custos desnecessários e valores baixos podem levar a falhas de graves conseqüências.
A tabela abaixo dá alguns critérios genéricos para coeficientes de segurança.
Propriedades do
material
Exatamente conhecido Exatamente conhecida Exatamente conhecidas
Bem conhecido
Bem conhecida
Exatamente conhecidas
Razoavelmente
Bem conhecido
Bem conhecida
conhecidas
Razoavelmente
Razoavelmente
Ensaiadas
conhecido
conhecida
aleatoriamente
Razoavelmente
Razoavelmente
Não ensaiadas
conhecido
conhecida
Pouco conhecido
Pouco conhecida
Não ensaiadas
Coeficiente Carregamento
1,2 - 1,5
1,5 - 2,0
2,0 - 2,5
2,5 - 3,0
3,0 - 4,0
4,0 - 5,0
Tensão no material
Ambiente
Totalmente sob controle
Estável
Normal
Normal
Normal
Variável
Observações:
• Cargas cíclicas devem ser dimensionadas pelo critério de fadiga (aqui não dado).
• Se houver possibilidade de choques, o mínimo coeficiente deve ser 2 multiplicado por um fator de choque (em
geral, de 1,5 a 2,0).
• Os dados da tabela são genéricos e muitas vezes subjetivos. Não devem ser usados em aplicações críticas e/ou
de elevada responsabilidade. Nestes casos, informações devem ser obtidas em literatura ou fontes
especializadas, normas técnicas, etc.
3-) Reservatório cilíndrico de parede fina
Um reservatório cilíndrico de raio r e espessura t é considerado de parede fina se r/t ≥ 10. Nessa condição,
podemos supor que as tensões se distribuem de maneira uniforme ao longo da espessura do cilindro.
Também é suposto que está sujeito a uma pressão interna
uniforme p, maior que a atmosférica e relativa à mesma, isto é,
pressão manométrica.
O quadrilátero vermelho da Figura 3.1 representa uma porção
elementar da parede do cilindro, que sofre ação de uma tensão ao
longo da circunferência α1 e uma tensão longitudinal α2.
Fig 3.1
Supomos o corte de uma porção cilíndrica de largura Δx (A da
Figura 3.1).
Se a porção cilíndrica é cortada diametralmente, a tensão σ1 atua na direção perpendicular às superfícies das
extremidades S1 (áreas vermelhas da Figura 3.1 B). Para o equilíbrio estático, a força devido a essas tensões
deve ser igual à força devido à pressão interna p. Assim,
2 σ1 S1 = 2 σ1 Δx t = p 2r Δx. Notar que a força devido à pressão é igual ao valor dela multiplicado pela área
frontal às extremidades das superfícies S1 (2r Δx) e não ao longo da circunferência.
Portanto, σ1 = p r / t #III.1#.
Para a tensão σ2, consideramos um corte transversal do cilindro
conforme Figura 3.2.
A tensão σ2 atua sobre uma coroa circular conforme região
vermelha no lado direito da figura. Como t é pequeno em relação a
r, podemos considerar sua área igual a 2 π r t. E a força para
equilibrar é igual à pressão interna multiplicada pela área do
círculo de raio r. Assim,
Fig 3.2
σ2 2 π r t = p π r2. Portanto, σ2 = p r / (2 t) #III.2#.
Por esta e pela igualdade #III.1# podemos concluir que a tensão determinante para dimensionamento é σ1, ou
seja, a tensão no sentido da circunferência do cilindro. Outro aspecto importante: junções (soldadas ou de
outros tipos) paralelas ao eixo do cilindro sofrem tensões iguais ao dobro das tensões em junções ao longo da
circunferência.
4-) Reservatório esférico de parede fina
Seja um reservatório esférico de raio r e espessura t de parede. A parede é considerada fina (r/t ≥ 10), de forma
similar ao cilíndrico do tópico anterior.
Se o reservatório é preenchido com um fluido sob pressão p
(relativa a atmosférica), a simetria sugere que as tensões σ são as
mesmas em quaisquer direções.
Fig 4.1
Considerando uma semi-esfera conforme lado direito da Figura
4.1, a tensão σ atua perpendicularmente à área vermelha
(aproximadamente igual a 2 π r t). E a força para manter a
condição de equilíbrio estático é igual à pressão interna
multiplicada pela área do círculo de raio r.
Assim, σ 2 π r t = p π r2. Ou σ = p r / (2 t) #IV.2#.
Observar que é igual à menor tensão calculada para o reservatório cilíndrico do tópico anterior. Por isso,
podemos supor que o reservatório esférico é o que suporta maior pressão com a menor quantidade de material.
5-) Algumas considerações sobre reservatórios
Além das tensões superficiais, reservatórios submetidos a pressões internas estão sujeitos a tensões radiais, que
variam do valor da pressão na superfície interna até zero na superfície externa. Na suposição de paredes finas
conforme tópicos anteriores, essas tensões são em geral de 5 a 10 vezes menores que as demais e podem ser
desprezadas.
As fórmulas dos dois tópicos anteriores valem para reservatórios sob pressão interna. No caso de reservatórios
submetidos a pressões externas (para vácuo por exemplo), falhas podem ocorrer antes da ruptura devido à
deformação das superfícies.
Essas fórmulas são as mais simples para reservatórios cilíndricos e esféricos. Existem várias outras
considerações a tomar no projeto dos mesmos (coeficientes de segurança, reforços em apoios e outros locais
como tampas e saídas de tubos, temperatura, corrosão, etc). Consultar normas técnicas e outras fontes sobre o
assunto.