pontos raio -método -posições

Lista 1
Física III
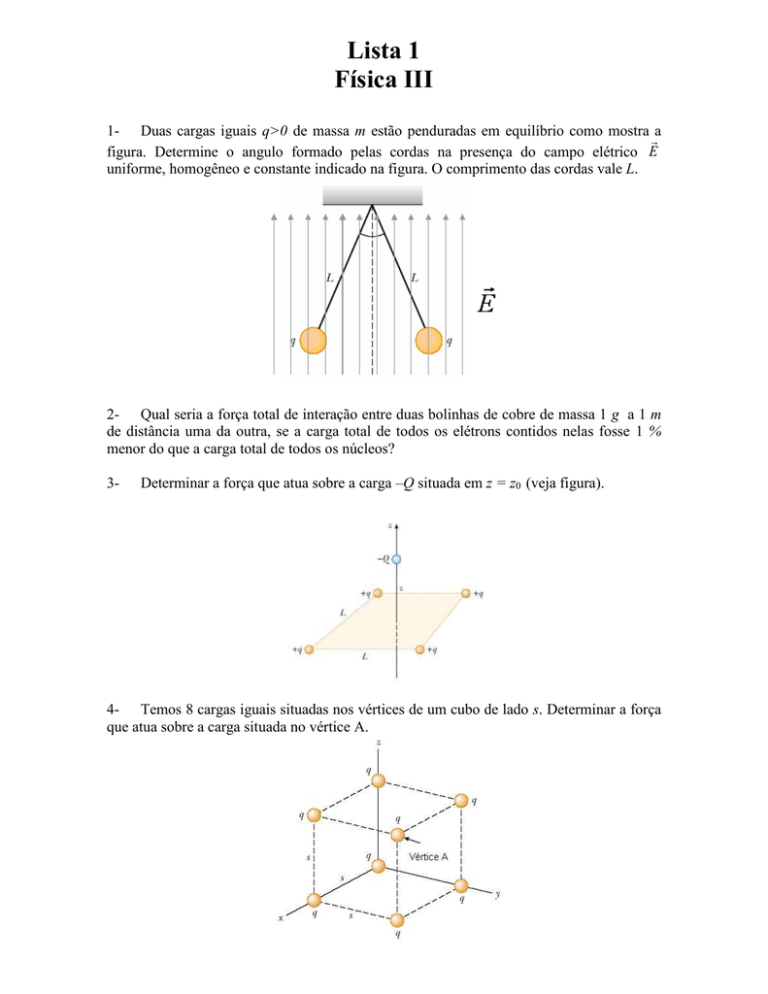
1- Duas cargas iguais q>0 de massa m estão penduradas em equilíbrio como mostra a

figura. Determine o angulo formado pelas cordas na presença do campo elétrico E
uniforme, homogêneo e constante indicado na figura. O comprimento das cordas vale L.
2- Qual seria a força total de interação entre duas bolinhas de cobre de massa 1 g a 1 m
de distância uma da outra, se a carga total de todos os elétrons contidos nelas fosse 1 %
menor do que a carga total de todos os núcleos?
3-
Determinar a força que atua sobre a carga –Q situada em z = z0 (veja figura).
4- Temos 8 cargas iguais situadas nos vértices de um cubo de lado s. Determinar a força
que atua sobre a carga situada no vértice A.
5- Um dipolo elétrico está constituído por duas cargas iguais de sinal contrario, situadas
a uma distância d=2a uma da outra. Este modelo é muito apropriado para descrever o
campo elétrico de moléculas como o HCl. Determine o campo elétrico do dipolo elétrico,
no ponto P representado na figura. Qual seria o valor deste campo para pontos situados em
y>>a?
6- Uma bolinha de massa m e carga q<0 gira pendurada de uma corda, com uma
velocidade angular  (veja figura). Determine o angulo que a corda forma com a

vertical na presença do campo elétrico E uniforme, homogêneo e constante.
 
**7- Nos pontos definidos pelos vetores r1 e r2 encontram-se duas cargas positivas q1 e

q 2 . Determinar a carga negativa q 3 e o vetor r3 do ponto do espaço onde esta carga deve

ser colocada, para que a força resultante que atua sobre qualquer uma das cargas seja 0 .
Campo elétrico de distribuições continuas de cargas.
1Um fio metálico, de comprimento l, está uniformemente carregado com uma carga
total q positiva. Determine a força com que ele atua sobre a carga Q negativa (veja a
figura).
2Um bastão fino de vidro é encurvado de modo a formar um semicírculo de raio R.
Uma carga +Q está distribuída uniformemente ao longo da metade superior, e uma carga Q ao longo da metade inferior, como mostra a figura. Determine o campo elétrico E, no
centro P do semicírculo.
3Uma carga Q distribuída uniformemente sobre um fio semicircular de radio a.
Calcular a força com que atua sobre uma carga Q colocada no centro (veja figura)

4Determine o campo elétrico E , num ponto P, localizado no eixo de um disco de
raio R e densidade superficial de carga    0 r (  0  constante ). O plano do disco é
perpendicular ao eixo x e o ponto P está a uma distância a do centro do disco.
5-
Repetir o problema anterior para as densidades superficiais de carga:
a)    0 r 2 b)  
0
r
c)  
0
r2
**6- Um fio uniformemente carregado com densidade linear de carga , possui as
configurações que aparecem nas figuras (a) e (b). Considerando que o radio de curvatura R
é muito menor que o comprimento do fio, determinar o módulo do campo elétrico no ponto
P em ambos os casos.
7No centro de um anel fino de radio R , no qual encontra-se distribuída
uniformemente uma carga -q , temos uma carga puntiforme q. Determinar o módulo do
vetor campo elétrico num ponto do eixo do anel, situado a uma distancia x do seu centro, se
x>>R.
**8- Um sistema está composto por um anel carregado de radio R e um fio
uniformemente carregado muito longo, situado no eixo do anel, de forma tal que um de
seus extremos coincide com o centro do anel. O anel tem uma carga q e o fio tem uma
densidade linear de cargas Determinar a força de interação entre o anel e o fio.
**9- Um anel de cargas de raio a, possui uma carga Q> 0 uniformemente distribuída. No
eixo do anel, a uma distancia l, temos uma carga q<0 com massa m. Se em t=0 a carga q
for liberada, determinar a velocidade com que passa pelo centro do anel. Quanto tempo a
carga gasta para chegar ao centro do anel? Como poderíamos caracterizar o equilíbrio neste
ponto?