Exp_3CEE_Circuito_Aberto_E_Curto

CONVERSÃO ELETROMECÂNICA DE ENERGIA
ENSAIOS DE CURTO-CIRCUITO E CIRCUITO ABERTO
PARA DETERMINAÇÃO DOS PARÂMETROS DE TRANSFORMADORES
Parâmetros dos Transformadores
Relação de Transformação:
É a relação que existe entre a quantidade de tensão e corrente entre o primário e a relação de quantidade de tensão e
corrente do secundário de um transformador.
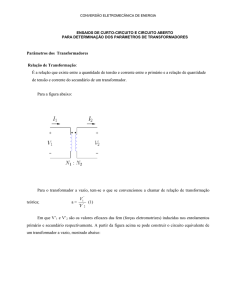
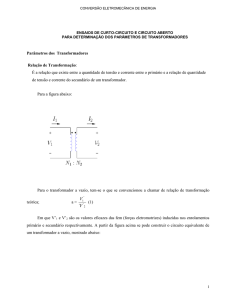
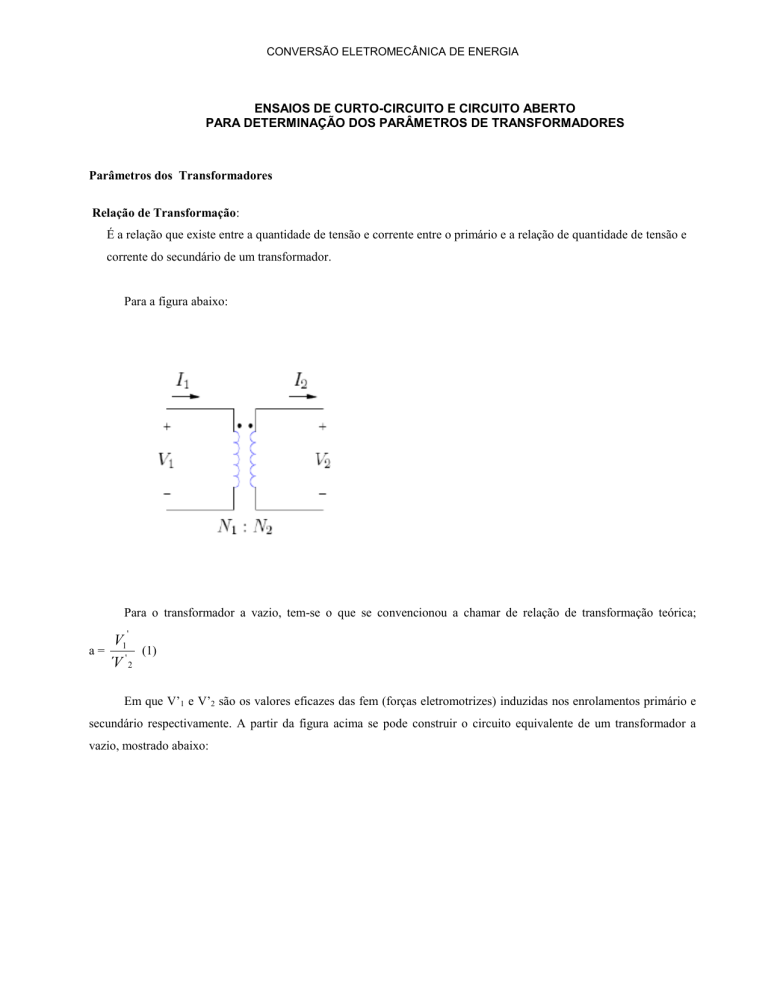
Para a figura abaixo:
Para o transformador a vazio, tem-se o que se convencionou a chamar de relação de transformação teórica;
'
V
a = 1' (1)
´V 2
Em que V’1 e V’2 são os valores eficazes das fem (forças eletromotrizes) induzidas nos enrolamentos primário e
secundário respectivamente. A partir da figura acima se pode construir o circuito equivalente de um transformador a
vazio, mostrado abaixo:
CONVERSÃO ELETROMECÂNICA DE ENERGIA
Onde:
r1 → resistência do enrolamento primário;
x1 → reatância de dispersão do enrolamento primário = 2 f L1
V’1 → fem (força eletromotriz) induzida no primário;
r2 → resistência do enrolamento secundário;
x2→ reatância de dispersão do enrolamento secundário = 2 f L2
V’2 → fem (força eletromotriz) induzida no secundário.
Xm= Reatância indutiva do núcleo
Rc= Perdas do ferro
CONVERSÃO ELETROMECÂNICA DE ENERGIA
Modelo real do transformador
1)
I
V '1 N 1
=
= 2 = a de isto V’1 = aV’2
'
I1
V 2 N2
2)
Z1 = a2
Z2
3)
V1 = I1(R1 + jXL1) + V’1
4)
V’2 = I2(R2 + jXL2) + ( I 2 Z L )
5)
aV’2 = aI2(R2 + jXL2KZL) + I2KZL= V’1
Z1=
V1
I1
e
Z2=
V2
I2
Como V’1 = a V’2 e se remplazando 5 em 3
V1 = I1(R1 + jXL1) + aI2(R2 + jXL2) + I2aZL
Lembrando que I2 = aI1
V1 = I1(R1 + jXL1) + a2I1(R2 + jXL2) + I1a2ZL
Separando a parte real da imaginaria
6)
V1 = I1(R1 + a2R2) + I1j (XL1 + a2XL2) +I1 a2ZL
Onde :
Re1 = (R1 + a2R2)
= Resistência equivalente , referida ao primário
XLe1 = (XL1 + a2XL2) = Reatância indutiva equivalente
V1 = I1( Re + jXLe + a2ZL)
CONVERSÃO ELETROMECÂNICA DE ENERGIA
Da igualdade dos números complexos
8)
Z 1 = a2
Z2
9)
Z1 = a2Z2
(R1 + jXL1) = a2(R2 + jXL2)
Igualdade da parte real
10)
R1 = a2R2
11)
XL1 = a2XL2
Por tanto
Re1 = (R1 + a2 R2)
Re1 = 2a2R2 = 2R1 , do mesmo jeito para a reatância indutiva equivalente:
XLe1 = 2a2XL2 = 2XL1
Determinação dos parâmetros no ensaio de curto circuito
Re1
2a 2
R2 =
XL2 =
XLe1
2a 2
R1 =
XL1 =
Re1
2
XLe1
2
Para o circuito primário, tem-se uma corrente de curto circuito Icc medida e uma tensão de curto circuito Vcc ,
também medida e a potencia de curto circuito.
Ze =
Vcc
I cc
Impedância equivalente calculada a partir dos valores de corrente e tensão de curto medidos
Pcc = I2ccRe1; Potencia de curto circuito, podemos calcular Re
Re1 =
Pcc
I cc2
CONVERSÃO ELETROMECÂNICA DE ENERGIA
12)
Ze1 =
Re 2  XLe 2
XLe1 =
Ze 2  Re 2
2a2R2 = Re1
2a2XL2 = XLe1
2R1 = Re1
2XL1 = XLe1
Determinação dos parâmetros no ensaio de Circuito aberto
Como vemos no desenho do modelo de transformador real existe uma corrente de magnetização, necessária para
que o transformador trabalhe , a potencia dissipada por esta corrente é chamada de perdidas de ferro.
Como o fio de cobre apresenta uma resistência ôhmica pura ao circular uma corrente por ela se produze uma
potencia por efeito Joule I2Rcu, esta potencia perdida no cobre depende da magnitude da corrente que circula. No
entanto a perdida de ferro e um valor fixo.
Pfe = Potencia indicado pelo watímetro quando o transformador esta em aberto e tem um valor fixo.
Pcu = Potencia dissipada no fio de cobre em função da magnitude da corrente que circula.,
CONVERSÃO ELETROMECÂNICA DE ENERGIA
Modelamento matemático de transformador Monofasico
Nome: .......................................................................
Modelar o nucleo
1- A partir dos valores lidos, determinar a resistência análoga as perdas de ferro
2- Determinar a reatância e indutância do núcleo
Modelar as resistencias de bobinado e reatâncias de dispersão
3- Calcule a impedância do transformador
4- Calcule a Resistencia equivalente
5- Calcule a resistência primaria e secundaria
6- Calcule a reatância equivalente
7- Reatancias de dispersão primaria e secundaria
8- Modelo completo referido ao primário
9- Modelo completo refletido ao secundário
10- As quedas de tensão no transformador com cargas de 500W, 500VA capacitivos e 500VA indutivos e o fasor
de tensão de saída no secundário (use modelo referido ao secundário)
Aplicação do modelo matematico
11- Calcule a impedância percentual referida ao primario e secundario (use os valores nominais para definir as
bases)
12- Calcule o fusível para proteger o secundário
13- O modelo apresentado leva em consideração a saturação magnética?
14- Para obter o modelo matemático de um transformador trifásico que considerações deve fazer para a
conexão estrela e triangulo?