gabarito - Walter Tadeu

MINISTÉRIO DA EDUCAÇÃO - COLÉGIO PEDRO II – UNIDADE SÃO CRISTÓVÃO III
NOME: GABARITO
DATA: _______/ __________/ 2008
TURMA: ___________
PROF. WALTER TADEU
ATENÇÃO: Este teste pode ser realizado em grupo com até 5 alunos. O objetivo é que vocês possam discutir, entre
si, possibilidades de resolução, dirimir dúvidas que ainda possuam e que individualmente não foi possível. Participem
o máximo que puderem. Não desperdicem a chance de aprender com o colega. De alguma forma, mostrem sempre o
desenvolvimento ou argumento na solução. Boa sorte!
TESTE: FUNÇÃO E EQUAÇÃO EXPONENCIAL – 2ª SÉRIE - GABARITO
(VALE 1,0 PONTO)
1) Uma população de bactérias começa e dobra a cada 3 horas. Assim, o número de bactérias após t horas é dado pela
t
3
função n(t )  100.2 . Nessas condições, pode-se afirmar que a população será de 51200 bactérias depois de quanto
tempo?
Solução. A função é uma exponencial com variável t. Pela informação o número de bactérias dobra a cada 3
3
3
1
horas. Isto é: n(3)  100.2  100.2  100.2  200. Repare que no tempo inicial n(0) o valor é 100 (a metade).
Calcular o tempo para a população ser 51200 bactérias é calcular t tal que n(t) = 51200.
t
n(t )  51200  51200  100.2 3 . Escrevendo 51200 na forma 512 x 100 e usando potências de 2, temos:
t
t
51200  512.100  2 9.100  100.2 3  2 9.100  2 3  2 9 . Igualando os expoentes, temos:
t
 9  t  27.
3
Resposta: A população será de 51200 bactérias em 27 horas ou 1 dia e 3 horas.
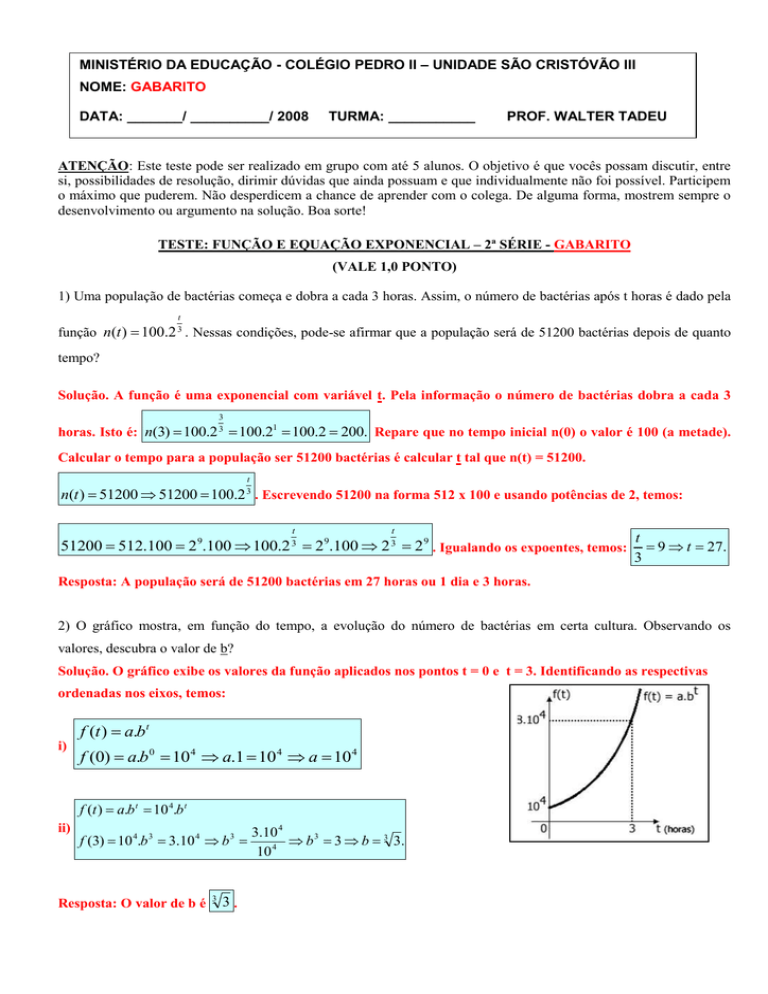
2) O gráfico mostra, em função do tempo, a evolução do número de bactérias em certa cultura. Observando os
valores, descubra o valor de b?
Solução. O gráfico exibe os valores da função aplicados nos pontos t = 0 e t = 3. Identificando as respectivas
ordenadas nos eixos, temos:
f (t )  a.b t
i)
f (0)  a.b 0  10 4  a.1  10 4  a  10 4
f (t )  a.b t  10 4.b t
ii)
3.10 4
f (3)  10 .b  3.10  b 
 b 3  3  b  3 3.
4
10
4
3
4
Resposta: O valor de b é
3
3
3.
3) Numa população de bactérias, há P(t )  10 9.43t bactérias no instante t medido em horas ou fração da hora. Se
inicialmente existem 109 bactérias, quantos minutos são necessários para que se tenha o dobro da população inicial?
Solução. A função é uma exponencial com variável t. Pela informação o número de bactérias no tempo inicial,
P(0) vale P(0)  10 9.4 3( 0)  10 9.4 0  10 9.1  10 9 . Calcular o tempo para a população dobre é calcular t tal que
P(t) =2.(109). Temos: P(t )  2.(10 9 )  10 9.4 3t  2.(10 9 )  4 3t 
2.(10 9 )
 4 3t  2 .
9
10
3t
2 3t
6t
Escrevendo 43t em potências de 2, temos: 4  (2 )  2  2  6t  1  t 
1
(hora )  10 min .
6
Resposta: A população será o dobro em 30 minutos.
4) Encontre os valores das incógnitas em cada uma das equações:
Soluções.
a) 10
x 2 3
2
2
1
1
x 2 3

 10 x 3  2  10 x 3  10 2
1 10

Resposta: x  1 ou x  1
100
10
100
2
2
x  3  2  x  1  x   1
(3 2.2) y
 2 x .3 y 1  3 2 y .2 y .2 1  2 x .3 y 1  3 2 y .2 y 1
2
2y
Resposta: x  2 e y  1
 3  y  1  2 y  y  1
2 x .3 y 1 
x
b) 2 .3
y 1
18 y y 1

3
2
2 x  2 y 1  x  y  1  x  1  1  x  2
c) 5 4 x 1  5 4 x  5 4 x 1  5 4 x  2  480
5 4 x 1  5 4 x  5 4 x 1  5 4 x  2  480  5 4 x .5 1  5 4 x  5 4 x .51  5 4 x .5 2  480
1
1
1  5  25  125
5 4 x (5 1  1  51  5 2 )  480  5 4 x (  1  5  25)  480  5 4 x (
)  480 Resposta: x 
2
5
5
480
5
1
54x 
 5 4 x  480.  5 4 x  25  5 4 x  5 2  4 x  2  x 
96
96
2
5
9 x  3 x 1  4  (3 2 ) x  3 x 1  4  (3 x ) 2  3 x .3  4  (3 x  y )
2
x
d) 9 x  3 x 1  4 y  3 y  4  0  ( y  1)( y  4)  0  y  1  3  1  x  0. Resposta: x  0
y  4(impossível  3 x  0)
5) Se A x  y  2 e A3 y  8 , calcule o valor de Ax.
 x y
Ax
A

2

2
Ax
Ax

y
 y 2
 2  A x  4. Resposta: A x  4
A

2
A
 A3 y  8  ( A y ) 3  2 3  A y  2
