Lista de exercício de física II

Universidade Federal Rural do Semi-árido - UFERSA
Lista de exercício de física II
Profª: Jusciane da Costa e Silva
01) Uma corda de massa desprezível está esticada horizontalmente entre dois
suportes separados por 3,44 m. Quando um objeto pesando 3160 N é pendurado
no centro da corda, ele arqueia por 35 cm. Qual é a tensão na corda?
02) Um arco é puxado em seu ponto médio até que a tensão na corda fica igual à
força exercida pelo arqueiro. Qual é ângulo entre as duas metades de corda?
03) Na Fig. Abaixo, uma esfera uniforme de massa m = 0,85 kg e raio r = 4,2 cm
são mantidos em repouso por uma corda de massa desprezível presa a uma
parede sem atrito a uma distância L = 8,0 cm acima do centro de esfera.
Encontre (a) a tensão na corda e (b) a força da parede a esfera.
04) A fig. Abaixo esta em equilíbrio, com a corda do centro exatamente na
horizontal. O bloco A pesa 40 N, o bloco B pesa 50 N, e o ângulo teta é 35°.
Encontre (a) a tensão T1, (b) a tensão T2, (c) a tensão T3 e (d) o ângulo teta.
05) Na Fig. Abaixo, uma viga uniforme e peso igual a 500 N e com 3 m de
comprimento está suspensa horizontalmente. No lado esquerdo ele está presa a
uma parede por uma dobradiça; à direita ela está presa por um cabo parafusado
na parede a uma distância D acima da viga. O cabo se rompe com uma tensão
mínima de 1200 N. (a) Que valor de D corresponde a esta tensão? (b) Para que o
cabo não se rompa, D deve aumentar ou diminuir em relação a este valor?
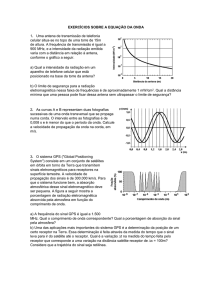
06) A Fig. Abaixo mostra a curva tensão-deformação para o quartzito. Quais são (a)
o módulo de Young e (b) o valor aproximado do limite elástico para este
material?
07) Uma haste de alumínio horizontal com 4,8 cm de diâmetro se projeta 5,3 cm
além da parede. Um objeto de 1200 kg esta suspenso na extremidade da haste. O
módulo de cisalhamento do alumínio é 3 x 1010 N/m2. Desprezando a massa da
haste, encontre (a) a tensão de cisalhamento sobre a haste e (b) a deflexão
vertical da extremidade da haste.
08) Na Fig. Abaixo, um tijolo de chumbo repousa horizontalmente sobre os
cilindros A e B. As áreas das faces superiores dos cilindros estão relacionadas
por AA = 2AB; os módulos de Young dos cilindros estão relacionados por EA =
2EB. Os cilindros tinham comprimentos idênticos antes que o tijolo fosse
colocado sobre eles. Que fração da massa do tijolo é suportada (a) pelo cilindro
A e (b) pelo cilindro B? As distâncias horizontais entre o centro de massa do
tijolo e os eixos dos cilindros são dAe dB. (c) Qual é a razão dA/dB?