EXPLORANDO O DERIVE (II)

EXPLORANDO O DERIVE (II)
Por Jorge Pato
Estudo gráfico de funções
O Programa Derive For Windows é uma excelente ferramenta de trabalho no
domínio das funções.
Vamos divulgar, no seguimento da parte I, alguns resultados da exploração de funções
em ambiente gráfico. Escolhemos para essa primeira abordagem as funções quadráticas.
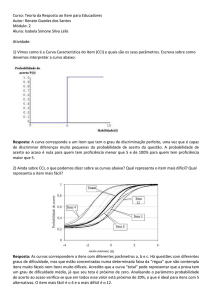
Tomemos para exemplo as funções quadráticas f e g definidas do seguinte
modo:
f(x) = x2  x + 3 ;
g(x) =  x2 + x  3
Editemos cada uma delas no ambiente algébrico
Author: expression ... f(x) := x^2  x + 3
Author: expression ... g(x) :=  f(x)
e passemos de seguida ao ambiente gráfico
‘clicando’ no botão
. Aparece no visor
o referencial cartesiano e a barra das
ferramentas de uso gráfico. O comando Plot
ou o botão
abaixo do comando Plot são
ferramentas de representação gráfica.
A configuração da janela para controlo e definição do gráfico é feita no ‘menu’
Set: Range.
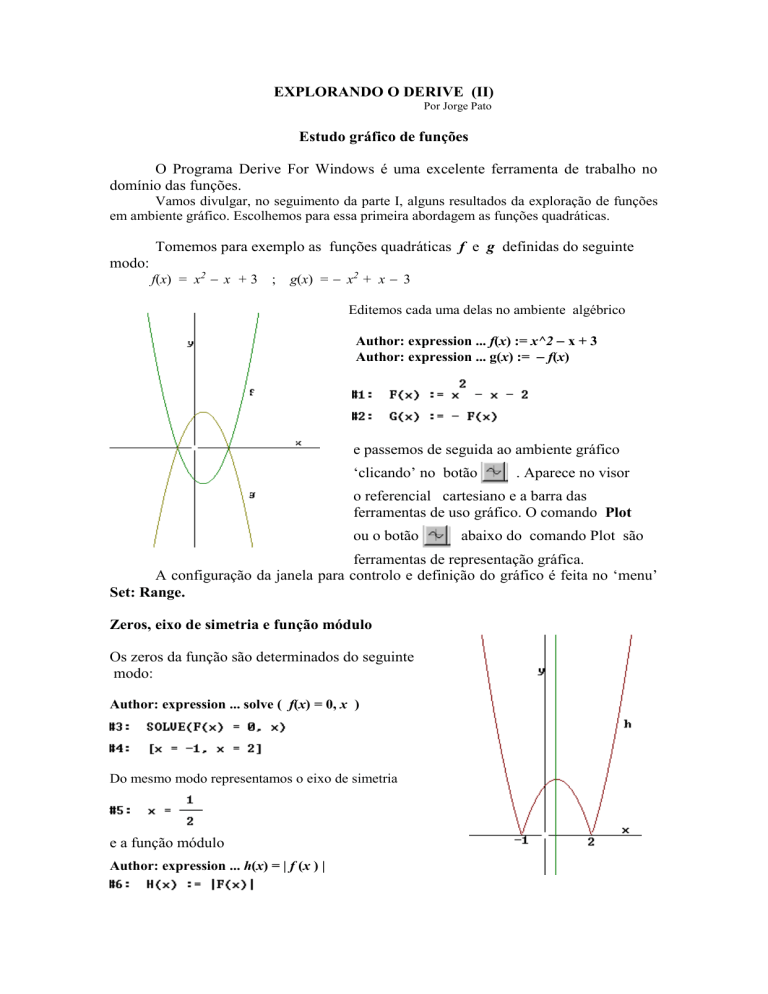
Zeros, eixo de simetria e função módulo
Os zeros da função são determinados do seguinte
modo:
Author: expression ... solve ( f(x) = 0, x )
Do mesmo modo representamos o eixo de simetria
e a função módulo
Author: expression ... h(x) = | f (x ) |
O eixo de simetria não depende da variação do termo independente do trinómio
Consideremos a família de funções quadráticas definida por f(x) = x2 + x + c ,
sendo c um parâmetro real. Usemos a instrução vector para representar funções numa
parte do domínio, fazendo variar c em passos desejados.
Editemos a seguinte expressão no ambiente algébrico, atribuindo, para isso, ao
parâmetro c valores do intervalo -3, 3, tomados em passos de 1 unidade.
Author: expression ... Vector(x^2+x+c,c,-3,3,1) OK  Simplify:basic (ou )
Podemos assim observar, no ambiente gráfico,
a propriedade enunciada: o eixo de simetria não
depende da variação do termo independente do
trinómio.
Simetrias em relação aos eixos referenciais
1. Simetrias em relação ao eixo oy
Fixemos os parâmetros a e c na família de funções quadráticas f(x) = ax2 + bx + c
e façamos variar o parâmetro b.
Sejam por exemplo a = 1, c = 1 e b{-2 , 2}. No ambiente algébrico editemos as
funções utilizando a instrução vector.
Procedimentos:
Passando ao ambiente gráfico obtemos
as representações de duas parábolas
simétricas em relação ao eixo oy.
Dos ramos simétricos obtemos as
seguintes funções:
Vamos agora fixando os parâmetros a e b, a = -1 e c = 1 e fazendo variar b entre
- 4 e 4, em passos de 1. Ver fig.1.
fig1
fig 2
A figura 2 representa uma família de funções pares, sendo, para isso, o argumento da
família tomado em valor absoluto.
2. Simetrias em relação ao eixo ox
Dado um gráfico de uma função quadrática l , o gráfico simétrico em relação ao
eixo ox é dado pela função  l .
Representemos graficamente as funções l(x) = x2 + x + 1 e  l(x).
Procedimentos:
Os procedimentos são análogos para uma
família de funções.
Família de parábolas tangentes num ponto
Vamos estudar uma particularidade interessante de uma família de parábolas
tangentes num ponto. Esta família é obtida pela fixação dos parâmetros b e c ,
fazendo variar o parâmetro a, (a  0). Consideremos, por exemplo, a seguinte
família f(x) = ax2 + x + 1 e atribuamos ao parâmetro a os valores de {-3,-2,1,4}.
Se numa quadrática f(x) = ax2 + bx + c fixarmos
os parâmetros b e c, os gráficos das funções
que se obtêm por variação de a são tangentes
no ponto (0, c) e à recta y = bx + c no mesmo
ponto.
Se fixarmos o parâmetro c e fizermos variar os
outros por valores simétricos, por exemplo, c = 1 e
a{-1,1} e b{-2,2}, obtemos um conjunto de
simetrias que se intersectam e se contactam num
ponto.