6. Acessibilidade na Península ibérica

ACESSIBILIDADE ECONÓMICA E POTENCIAL DE MERCADO:
EVIDÊNCIA DA PENÍNSULA IBÉRICA
Armando José Garcia Pires*
ISEG/UTL
Fevereiro 2001
RESUMO:
Este trabalho apresenta uma metodologia para quantificar acessibilidade económica no contexto de
um modelo de geografia económica. Ao contrário das medidas tradicionais de potencial de mercado
desenvolvidas de uma forma ad-hoc sem uma estrutura teórica-económica sólida por de trás, a presente
metodologia tem os seus alicerces num modelo que explicita a estrutura de mercado, agentes e
interacções estratégicas. A aplicação do modelo desenvolvido ao caso das regiões NUTS 2 da Península
Ibérica permite tirar algumas conclusões prévias. Em primeiro lugar em termos de centralidade a
economia espanhola tem uma grande vantagem sobre a economia portuguesa. De facto Portugal aparece
neste estudo quase como uma economia periférica da espanhola, onde nem sequer a região de Lisboa
(região mais desenvolvida de Portugal) consegue ter no conjunto da Península Ibérica uma importância
relevante em termos de potencial económico. Comparativamente às regiões espanholas, a região de
Lisboa apenas tem uma performance marginalmente superior à pior região da Espanha (Galiza). O pico
de acessibilidade é atingido pela região de Madrid sendo seguida de perto pelo País Vasco e pela
Catalunha, formando estas três regiões os principais centros económicos da Península Ibérica. Testes de
sensibilidade dos parâmetros confirmam a robustez dos resultados. Em segundo lugar um cenário de
integração completa entre a economia portuguesa e a economia espanhola não aparenta ser benéfica para
uma parte considerável das regiões. Tal como previsto pela literatura na “nova” geografia económica as
regiões mais beneficiadas são as mais avançadas, evidenciando portanto efeitos de “lock-in” e de
“causalidade cumulativa”.
Palavras Chave: Geografia Económica; Acessibilidade; Potencial de Mercado; Península Ibérica.
Classificação JEL: C68; F12; F15; R12; R13.
e-mail: [email protected]
*
O autor agradece ao Professor Renato Flôres e à Professora Paula Fontoura pelos valiosos comentários e interessantes discussões
durante a preparação deste trabalho. Esta pesquisa foi suportada por uma bolsa da Fundação para a Ciência e a Tecnologia (Praxis
XXI/BM/17786/98). Quais queres erros ou omissões são no entanto da minha inteira responsabilidade.
1.
INTRODUÇÃO
Indicadores de acessibilidade têm tido uma série de aplicações em pesquisa
empírica em várias áreas da economia. Nomeadamente, em economia dos transportes
para avaliar investimentos em infra-estruturas de transporte1; economia regional como
método de cálculo do potencial de mercado de regiões ou localizações2; em economia
internacional para prever os efeitos espaciais da integração económica3; e mais
recentemente na literatura em geografia económica estes tem sido embebidos em
regressões econométricas para analisar os determinantes de localização industrial e
crescimento regional4.
Uma medida típica de acessibilidade económica em pesquisa empírica é o índice
potencial de mercado (Harris, 1954). Para uma dada região r o potencial Pr é definido
como:
Pr   M s f crs 
s
(1)
onde M s é a “massa” na região s , c rs a distância económica entre a região r e s , e
f c rs  uma função decrescente da distância5. Como com Pr se pretende medir o
potencial de mercado de uma região a variável M s denota a dimensão de mercado na
região s 6. A distância económica c rs pode representar vários custos relacionados com a
distância (transporte, tempo, tarifas, tarifas não-pautais e diferenças culturais).
No entanto, apesar da análise potencial de mercado se ter revelado uma
ferramenta importante em pesquisa espacial aplicada, esta não pode ser justificada com
base na teoria económica. Para além do mais não é possível através desta dizer quais
serão as consequências no rendimento, emprego, ou até mesmo bem-estar resultantes de
uma alteração no potencial de mercado de uma localização (resultante por exemplo de
uma diminuição nos custos de transporte). Como tal é desejável desenvolver índices de
1
Ver por exemplo Vickerman (1991).
2
Ver por exemplo Harris (1954); e Keeble, Offord, e Walker (1988).
3
A ideia de base desta abordagem, da qual Clark, Wilson e Bradley (1969) foram pioneiros, é a de que a integração económica
reduz a distância económica e portanto favorece as regiões que comparativamente ganham mais em temos de acessibilidades a
mercados.
4
5
6
Ver por exemplo Hanson (1998); e Pires (1999).
f crs   e  crs
ou
f c rs   c rs
são especificações típicas para a função de distância.
Usualmente mede-se a “massa” de uma região pelo seu produto regional.
acessibilidade que tenham um claro significado económico, e que sejam derivados
explicitamente de modelos teóricos de interacção económica espacial.
O objectivo deste trabalho é demonstrar que tal é possível no enquadramento de
um modelo espacial de concorrência imperfeita com rendimentos crescentes à escala e
custos de transporte. Para tal vamos seguir de perto o trabalho de Bröcker (1998b,c) em
equilíbrio geral espacial, e em particular Bröcker (1998a) que analisa a questão da
acessibilidade em equilíbrio geral.
Para além desta secção este trabalho tem mais oito secções. Na secção seguinte é
apresentado o modelo de geografia económica. A secção 3 introduz a questão da
acessibilidade no contexto do modelo apresentado. É demonstrado que algumas das
relações económicas presentes no modelo (como os preços) estão relacionados com
indicadores de potencial de mercado e medidas de bem-estar teórico. Com base nestas
derivações a secção 4 discute o modelo em causa. Na secção 5 o método de calibração
do modelo é analisado, sendo esta posteriormente utilizada na secção 6 para descrever a
acessibilidade na Península Ibérica. Na secção seguinte com base nos resultados da
calibração são realizados algumas análises de sensibilidade e simulações para dados
regionais da Península Ibérica. O trabalho conclui com algumas considerações sobre a
abordagem aqui realizada.
2.
MODELO DE GEOGRAFIA ECONÓMICA
O modelo espacial utilizado neste estudo descende directamente dos modelos
desenvolvidos na última década pela chamada “Nova” Geografia Económica. Esta
literatura foi iniciada pelo artigo de Krugman de 1991 “Increasing returns and economic
geography”, e foi posteriormente desenvolvida por este e outros como Venables (1996),
e Fujita e Thisse (1996)7.
O modelo que se vai apresentar considera um determinado número de firmas em
cada região, produzindo um cabaz de bens diversificados horizontalmente, usando como
inputs trabalho, capital, e um bem compósito intermédio. Existe neste cabaz um número
potencial elevado de tipos de bens produzíveis (apesar de em equilíbrio o mais provável
ser que nem todos os bens sejam produzidos). Aos olhos das firmas e consumidores,
cada um dos tipos de bens é substituto imperfeito de todos os outros tipos de bens. Cada
firma em equilíbrio produz apenas uma variedade, e estas entre si praticam concorrência
monopolística. As firmas maximizam os lucros tomando em conta a responsividade
7
Ver também Fujita, Krugman e Venables (1999).
preço da variedade que produzem. A entrada e saída de firmas é permitida, e o número
de variedades existente no mercado (e consequentemente o número de firmas) é
determinado endogenamente pela condição de lucro zero.
O bem intermédio é composto por todas as outras variedades existentes no mercado
no momento. Todas as variedades entram simetricamente na função de produção, o que
significa que não há preferência por variedades específicas. Seguindo Krugman (1993) a
produtividade marginal de uma variedade é decrescente, de tal modo que maior
variedade de bens diferenciados intermédios aumenta a produtividade.
O pagamento dos factores das firmas de propriedade regional vai directamente para
os consumidores dessa região, que gastam o seu orçamento em bens consumíveis. Os
consumidores no modelo também representam toda a procura final, incluindo consumo
público e investimento.
A dimensão espacial é introduzida neste modelo na forma tradicional, considerando
que tem que se incorrer em custos para fazer comércio. Estes custos de fazer comércio
aumentam com a distância entre os mercados consumidores e produtores. No entanto ao
contrário do usual nesta literatura, não são considerados custos de transporte na forma
de “iceberg”.
Dada esta estrutura, o modelo utilizado é um de “quase” equilíbrio geral no sentido
em que este é caracterizado pelos agentes afectados a cada região, tecnologias,
preferências, e dotações atribuídas a cada agente, pela delimitação de mercados e pela
estrutura de mercado.
2.1.
PRODUÇÃO
A produção é modelada como um processo em dois estágios. No primeiro estágio
as firmas na região r produzem um bem homogéneo (bem primário), usando uma
tecnologia Cobb-Douglas e tendo como inputs, trabalho, capital e um bem compósito.
Para uma firma “price-taker” o custo mínimo por unidade de produto do bem
homogéneo na região r é:
p r   r wr z r q r ,
(2)
com       1 , e onde wr denota a taxa salarial, z r a taxa de juro, e q r o preço do
bem compósito na região r . Os parâmetros  ,  , e  são as elasticidades parciais da
produção. Estes parâmetros igualam respectivamente a parte do trabalho, capital e bens
intermédios no valor da produção. Por sua vez o parâmetro  r representa as diferenças
regionais no nível de produtividade. Dado um vector de inputs constante, o nível de
produção é proporcionalmente inverso a  r .
No segundo estágio de produção, as firmas tomam o bem homogéneo como bem
intermédio para a produção de diferentes variedades de bens finais8. Para produzir x
unidades de uma variedade do bem diferenciado a firma necessita de f  cx unidades
do bem primário9. Esta é a conhecida função de custo linear, onde f denota os custos
fixos, e c o custo variável unitário (ambos expressos em termos de unidades do bem
primário10. Usando a relação de Amoroso-Robinson-Marshall, uma firma maximizadora
do lucro (tomando p r como adquirido) estabelecerá o preço dos bens finais tal que:
r 

 1
cp r
(3)
onde  é a elasticidade preço da procura (com   1). Como com livre entrada e saída
de firmas os lucros em equilíbrio são zero, o lucro  r deve ser igual aos custos
marginais. Portanto vamos ter:
c
f


c
x  1
(4)
Resolvendo para x obtemos:
x
f
  1
c
(5)
Desta relação retira-se o número de variedades produzido na região r :
lr 
Xr
f
(6)
onde X r denota a quantidade do bem primário produzido em r .
8
Esta estrutura formal de modelar a produção é conhecida por concorrência monopolística e deve-se a Dixit Stiglitz (1977).
9
Ver Flôres (1997) para uma calibração dos parâmetros da função de custos. Os sectores considerados são: têxteis e couros;
madeiras; papel, produtos em papel e impressão; produtos minerais não metálicos; produtos metálicos, máquinas, materiais e
aparelhos eléctricos; produtos químicos; produtos alimentares, bebidas e tabaco; material de transporte.
10
Como tal o bem primário é neste modelo o numerário.
Uma unidade do bem compósito é constituída por variedades individuais de
acordo com um índice simétrico com elasticidade constante de substituição (índice
CES). Expressando este em forma dual vai significar que q s o preço por unidade do
bem compósito na região s é igual a:
1
1

1 
q s   l r  r rs  
 r

(7)
onde  denota a elasticidade de substituição entre variedades11, e  rs um factor mark-up
representando os custos de transferir os bens entre a localização r e s (com  rs  1 ).
2.2. CONSUMIDORES
Os consumidores em cada região r recebem como rendimento y r resultante do
empréstimo ás firmas regionais do trabalho e capital que possuem12. Todo o rendimento
obtido pelos consumidores é gasto na compra de bens de consumo. Os consumidores
têm preferências CES simétricas e homotéticas sobre as variedades com elasticidade de
substituição  , a mesma que no agregado dos bens intermédios por parte das firmas.
Portanto com rendimento y r a utilidade máxima que um consumidor representativo
pode obter é:
ur 
yr
qr
(8)
2.3. CUSTOS DO COMÉRCIO INTER-REGIONAL
Como já foi referido os custos de fazer comércio pretendem significar não apenas
custos de transporte mas quaisquer custos que tornem mais onerosa a transacção dos
bens no espaço (custos de transporte, custos de comunicação, barreiras comerciais). Os
custos de transporte podem tanto depender da quantidade transportada como do valor
dos bens. Neste último caso estão alguns dos custos de transferência inter-regional
11
Se o número de variedades é muito grande,

é também a elasticidade preço-procura para uma variedade individual tal como na
equação (3).
12
Na aplicação empírica deste modelo dado a ausência de dados, vamos ser obrigados a assumir que todo o serviço de factores
usado por firmas regionais vem de consumidores regionais. Na prática isto significa que não são considerados fluxos inter-regionais
de rendimentos de factores. Esta hipótese não é realista, pelo menos em relação ao rendimento do capital, mas como não é
conhecida a distribuição regional do rendimento do capital não é possível ultrapassar esta inconveniência.
relacionados especialmente com os custos de informação, e seguros. Nas análises
económicas usualmente assume-se que os custos do comércio dependem apenas na
quantidade dos bens comercializados, no entanto neste modelo vamos optar por fazer os
custos de transporte depender no valor comercializado uma vez que simplifica a análise.
O modelo considera dois tipos de custos de comércio: custos relacionados com a
distância, e custos relacionados com os impedimentos ao comércio internacional. Se
uma região r pertence a um país k e a região s ao país l (com k  l ) então o factor
mark-up representando os custos de transporte é:
 rs  exp g rs  kl
(9)
onde g rs denota a distância geográfica entre duas regiões,  mede os custos por
unidade de distância em percentagem do valor do bem, e  kl  1  0 o equivalente de
custos de comércio para todos os custos que resultam de um bem ter que ser exportado
do país k para o país l . Pretende-se capturar com este parâmetro todos os custos
relacionados por exemplo com tarifas, barreiras não pautais, e diferenças culturais13.
Os impedimentos ao comércio internacional podem ser expresso como
equivalentes de distância. Para um impedimento  kl , o equivalente em distância é igual
a log  kl  /  . Podemos então escrever:
 rs  exp crs 
(10)
com:
c rs  g rs 
log  kl 

(11)
Nesta especificação dos custos de transferência inter-regional é também
assumido que os custos de transporte de bens que chegam à região s , são pagos a uma
empresa transportadora, que consome o bem compósito, não tendo qualquer lucro nesta
actividade. Ou seja parte da despesa nos bens é usada para comprar o bem (quer este
seja para produção intermédia ou consumo final), e outra parte é para comprar bens que
vão para serviços de transporte.
13
De notar que
 kl  1 para k  l , e   1 para k  l .
2.4. EQUILÍBRIO
Da especificação de tecnologias, preferências, e estrutura de mercado, é agora
possível derivar o equilíbrio para um sistema fechado de regiões. Considera-se que cada
região está dotada com um montante fixo de trabalho e capital, que pertence aos
consumidores que residem na região. Os consumidores gastam todo o seu rendimento
dos factores, maximizando a sua utilidade. As firmas concorrem entre si sob
concorrência monopolística a la Chamberlain. O preço dos bens e factores, e o número
de variedades na economia ajustam até que os mercados atinjam o equilíbrio e os lucros
sejam zero.
O equilíbrio do modelo consiste nas equações do preço do bem compósito (2) e (7),
e três condições de equilíbrio para o mercado de bens, mercado do trabalho, e mercado
de capitais. Denotando o valor do produto como Vr  X r pr , e usando as equações (3) e
(6), a equação (7) pode ser escrita:
1

 1
q s    Vr p r  rs1 
 r

(12)
com  
1  c 


f   1
1
.
O equilíbrio do mercado de bens requer que para cada região r , o valor do
produto Vr seja igual ao valor da procura de bens nessa mesma região. Esta condição
conduz-nos à equação:
Vr  
s
Vr  p r rs 


V  p  

t
Vs
t ts
t
(13)
Para chegar a este resultado de notar que a forma CES na equação (7) implica
que a procura para uma variedade da região r por unidade do bem compósito comprado
em s ( d rs ) seja:
 q
d rs   s
  r rs




(14)
Como tal a parte da região r no valor da procura em s é igual a:
l r d rs r
V p  
 r r rs 
 lt d ts t Vt  pt ts 

t
t
(15)
Aqui é usado o facto de  r ser proporcional a p r de (3), e de que l r r ser
proporcional a Vr de (5). Por outro lado se o rendimento não é transferido entre regiões,
então o valor da despesa em bens na região s é igual a Vs , uma vez que as firmas
gastam todo o seu rendimento nos bens intermédios, custos de comércio e rendimento
de factores. O pagamento de custos de transporte, e o rendimento de factores vai todo
por seu lado para a compra de bens.
A procura de factores é obtida da equação (2) pelo Lema de Shephard. Logo as
condições para o equilíbrio do mercado de factores são:
Lr 
Vr
wr
(16)
e:
Kr 
Vr
zr
(17)
As condições de equilíbrio do sistema resumem-se às equações (2), (12), (13),
(16) e (17). Estas equações determinam p r , q r , Vr , z r , e wr para todo o r , dado o
stock de factores Lr e K r para todo o r .
3.
ACESSIBILIDADE E BEM-ESTAR
Como já foi referido o índice ur definido na equação (8) é o índice de bem-estar
regional neste modelo. Variações relativas de ur são iguais às medidas Hicksianas de
variação relativa do bem-estar. Numa análise estática comparativa os rendimentos
regionais para o equilíbrio de referência e para o equilíbrio contra-factual são obtidos
multiplicando o preço dos factores pela dotação de factores. Sendo u rR e u rC
respectivamente a utilidade no equilíbrio de referência e no equilíbrio contra-factual,
então o ganho de bem-estar no equilíbrio de referência em comparação com o equilíbrio
contra-factual é:
VERr 
u rC
1
u rR
(18)
onde VERr é a medida de Hicks de variação equivalente relativa (VER). A VER
representa a variação equivalente expressa como a parte no rendimento do equilíbrio
contra-factual. Similarmente o ganho de bem-estar no equilíbrio contra-factual em
comparação com o equilíbrio de referência é:
VCRr  1 
u rR
u rC
(19)
onde VCRr é a medida de Hicks de variação compensada relativa (VCR). A VCR é a
variação compensada expressada como percentagem no rendimento do equilíbrio de
referência. Uma medida alternativa pode ser a variação relativa em logaritmos, definida
por Bröcker (1998a) como:
 u rC
VRLr  log  R
 ur



(20)
O índice de bem-estar depende portanto nas dotações, tecnologias, e localização.
Para isolar os efeitos da localização, pode-se questionar qual o retorno real máximo em
factores de produção que uma firma representativa pode pagar em diferentes
localizações, desde que a tecnologia desta firma seja a mesma independentemente da
região onde esta está localizada.
Definindo a tecnologia da firma pela sua função de custo (2) mas substituindo
ur por uma constante:
_
p r   wr z r q r
(21)
Pode-se pensar nesta tecnologia como uma função Cobb-Douglas de dois níveis.
No nível mais baixo os serviços de trabalho e capital são combinados com um serviço
de factor com preço mr . No nível mais elevado este serviço do factor juntamente com o
bem intermédio produz o bem final. Então equivalente à equação (21), vai-se ter para o
nível mais baixo:

mr  wr z r

1
 
(22)
Para o nível mais elevado pode-se escrever:
_
p r   m1r  q r
(23) Daqui pode-se obter o retorno real do factor:
Fr 

mr  p r
 _
qr 
  qr





1
1
(24)
Portanto, Fr é uma função crescente com pr qr , que por seu lado é uma combinação
de um potencial da procura e oferta:
1
1
pr
 S r 1 Dr
qr
(25)
com o índice potencial de oferta:
S r  Vs p s exp 1   c sr 
s
(26)
e com o índice potencial de procura:
Dr   bsVs exp  crs 
s
(27)
onde bs é um índice potencial inverso:
bs 
V p
t

t
1
exp  cts 
t
(28)
Como facilmente se pode ver S r e Dr são similares aos índices potencial de
mercado padrão. A modificação em S r é que a oferta é ponderada por p s , ou seja a
oferta tem menor ponderação quanto maior o preço. Similarmente a modificação em Dr
é a de que a procura é ponderada por uma função potencial inversa, de tal modo que a
procura é menos importante quanto maior o potencial de ofertas concorrentes. De notar
que funções de distância diferentes aparecem em (26) e (27). No entanto nenhuma delas
é a habitual forma “iceberg”.
Outro facto interessante deste modelo é que p s e bs são os factores
compensadores de um modelo gravitacional com duas restrições descrevendo os fluxos
de comércio no modelo. Pelas equações (13), (28) e (10) o valor do comércio entre duas
regiões é:
t rs  Vr p r exp  c rs Vs bs
(29)
Em (13) e (28) t rs deve somar para Vr e Vs . Logo obtém-se as duas restrições:
Vs   t rs
r
(30)
e:
Vr   t rs
s
(31)
4.
DISCUSSÃO DO MODELO
Nas secções anteriores foi apresentado um indicador de acessibilidade semelhante à
formulação clássica em economia regional. No entanto este ao contrário das medidas
tradicionais de potencial de mercado, tem uma base teórica bem formada num modelo
espacial de concorrência imperfeita.
Para além desta vantagem teórica, este índice tem mais duas vantagens. Em
primeiro lugar a parametrização do modelo é menos arbitrária do que na abordagem
clássica. De facto os padrões de acessibilidade calculados pela forma tradicional podem
se alterar profundamente com alterações nos parâmetros da função de distância (ver
(1))14. Como as acessibilidades não são directamente observáveis não é possível estimar
ou calibrar directamente este parâmetro. No entanto na abordagem aqui apresentada
como os parâmetros em causa aparecem em equações descrevendo fluxos de comércio,
é possível verificar a calibração contra dados da economia real.
Por outro lado este modelo permite fazer análises de estática comparativa. Por
exemplo é possível avaliar os efeitos de maior integração económica na acessibilidade,
rendimento dos factores e bem-estar. A secção 2.4 descreve como avaliar alterações na
14
Bröcker (1989) discute esta questão.
remuneração dos factores; enquanto que a secção anterior explica como medir as
alterações de bem-estar. No presente estudo apenas vamos avaliar alterações na
acessibilidade e no bem-estar consequência da evolução do nível de integração
económica.
5.
CALIBRAÇÃO
O modelo é calibrado para um sistema de 20 regiões NUTS 2 que compõem a
Península Ibérica15. O quadro 1 apresenta uma lista das regiões NUTS 2 consideradas
neste estudo. Os dados usados para a calibração são emprego total por região, distâncias
inter-regionais, e PIB regional16. Todos os dados utilizados referem-se ao ano de 1994.
Com a excepção dos dados das distâncias inter-regionais, todos os restantes foram
retirados da base REGIO da EUROSTAT17. Os dados da distância inter-regional foram
compilados do CD-ROM “Route 66 Europe”. Este programa contém uma informação
geográfica vasta sobre todo o Continente Europeu, que inclui entre outras, informações
sobre distâncias por estrada entre cidades e localidades europeias. Como tal para
medirmos a distância inter-regional utilizamos a distância em quilómetros por estrada
entre cada par de regiões NUTS 2. A distância entre duas regiões é deste modo medida
como distância mais curta entre as cidades principais de cada uma das regiões NUTS 2
em causa. Considera-se a cidade principal de uma região NUTS 2, as mesmas que a
EUROSTAT enumera nas definições da base REGIO, o que em geral também
corresponde à cidade mais populosa dessa região18.
Quadro N.º 1 -
Península Ibérica: Regiões NUTS 1 e NUTS 2
País
Espanha
NUTS 1
Noroeste
NUTS 2
Galiza
Principado das Astúrias
Cantábria
Pais Vasco
Navarra
La Rioja
Aragão
Nordeste
15
Ver EUROSTAT (1996) para definição das regiões NUTS de Portugal e Espanha.
16
Bröcker (1998a) utiliza apenas PIB a nível do país, como tal
r
também é apenas calibrado a nível nacional. O presente estudo
calibra este parâmetro a nível regional.
17
Ver EUROSTAT (1996) para uma definição das variáveis utilizadas.
18
Exemplificando, considere-se as regiões NUTS 2 de Madrid e Lisboa e Vale do Tejo. A distância entre estas duas regiões não é
mais que a distância mais curta em quilómetros por estrada entre a cidade de Madrid e Lisboa.
Comunidade de Madrid
Centro
Este
Sul
Portugal
Continente
Comunidade de Madrid
Castela e Leão
Castilla-la Mancha
Estremadura
Catalunha
Comunidade Valenciana
Andaluzia
Região de Múrcia
Norte
Centro
Lisboa e Vale do Tejo
Alentejo
Algarve
Nota: Fonte EUROSTAT (1996)
Para calibrar o modelo apresentado nas secções anteriores é necessário conhecer o
valor de alguns dos parâmetros do modelo. Estes são: a elasticidade de substituição
entre variedades na procura intermédia e final (  ); a percentagem dos custos da
distância por unidade de distância (  ); as elasticidades de produção (  ,  e  ); os
impedimentos ao comércio internacional (  kl ); e o inverso do nível de eficiência
regional (  r ). No caso deste último parâmetro é necessário calibrar  r para as vinte
regiões consideradas19. A calibração fixa estes parâmetros juntamente com todas as
variáveis endógenas do modelo, que são o preço dos bens ( p r e q r ), o preço dos
factores ( wr e z r ), os valores da produção regional ( Vr ), e comércio inter-regional
( t rs ).
Começando pelo parâmetro  e  é possível observar que na equação (29) o
produto  representa o parâmetro de distância usualmente utilizado nos modelos
gravitacionais com uma função de distância exponencial. Estimativas deste parâmetro,
estão pelo menos para o comércio internacional, disponíveis na literatura (ver Bröcker e
Rohweder, 1990). No entanto a incidência geográfica deste estudo refere-se a comércio
inter-regional e não internacional. Bröcker (1984) estima o parâmetro em causa para os
fluxos de comércio entre regiões de seis países europeus. Infelizmente os países Ibéricos
não estão incluídos neste estudo. Para além do mais este estudo refere-se apenas ao ano
de 1970, os resultados podem portanto estar desactualizados20. Por seu lado Pires (1999)
19
Como já foi referido o estudo de Bröcker (1998a) apesar de ser um estudo de cariz regional, calibra este parâmetro apenas a nível
nacional.
20
McCallum (1995) também analisa através de um modelo gravitacional os fluxos internacionais e inter-regionais de comércio, só
que a incidência espacial deste estudo é a América do Norte (EUA e Canadá).
no contexto de uma “função potencial de mercado” semelhante à de Harris (1954) e de
um sistema de equações representantes do equilíbrio do modelo de geografia económica
de Krugman (1991) estima um impacto da distância entre 0.0002 e 0.0006 por
quilómetro para a economia espanhola21. Parece pois adequado aceitar uma estimativa
para este parâmetro que se situe neste intervalo. Seguindo Brocker (1998a) adoptamos
um valor de  =0.00046 por quilómetro para o parâmetro de distância.
Examinamos agora estes dois parâmetros em separado. Se consideramos apenas os
custos de transporte convencionais22, o valor para  seria segundo a literatura pequeno
em percentagem. De facto estudos empíricos nesta área reportam custos de transporte
médios na indústria transformadora que não excedem dois porcento do valor das vendas
(Keeble, Offord and Walker, 1988; Bröcker, 1998a, Davis, 1998). Mas isto implicaria
um valor para o parâmetro  na ordem das centenas, o que é pouco plausível pois isto
significaria estarmos a assumir substituibilidade perfeita no comércio inter-regional.
Portanto torna-se necessário considerar também os custos de transporte nãoconvencionais. Se tomarmos apenas os custos logísticos médios relacionados com a
distância, estes são segundo Bröcker (1998a,b) e Davis (1998) superiores a vinte por
cento do valor das vendas. Mas para além destes existem custos também relacionados
com a distância que não são considerados nos custos de logística como os custos de
contactos “cara-a-cara”. Para além disso a distância média no comércio inter-regional é
muito menor que milhares de quilómetros. Portanto um valor superior a vinte porcento
para  é justificável. Seguimos então Bröker (1998a) ao considerar um  igual
0.000046 por quilómetro. Consequentemente atribuímos um valor de 10 para o  23.
Como já foi referido, as elasticidades  ,  e  da função de produção, igualam
respectivamente as percentagens do trabalho, capital, e bens intermédios no valor do
produto. Estas percentagens são retiradas das contas nacionais de Portugal e Espanha,
onde a percentagem de trabalho é 28 porcento, a percentagem do capital é 12 porcento,
e a percentagem de bens intermédios é 60 porcento.
Tomando em consideração o valor para  kl pode-se argumentar que este parâmetro
em princípio não deveria entrar na presente análise, uma vez que Portugal e Espanha
21
O estudo incide sobre os anos 1981-1982-1983; 1988-1989-1990; e 1993-1994-1995.
22
Os custos de transporte são normalmente divididos em duas categorias: custos de transporte convencionais; e custos de transporte
não-convencionais (Davis, 1998). Os primeiros referem-se aos custos associados com seguros, fretes, e tarifas. Os segundos são
outros custos (normalmente de mais difícil mensuração) relacionados com o transporte dos bens e distância, tal como barreiras não
tarifárias e custos de informação.
23
Outros estudos de equilíbrio geral e parcial como o de Gasiorek, Smith, e Venables (1994); Bröcker (1998a,b); e Bröcker e JägerRoschko (1996) também trabalham com uma estimativa de 10 para o parâmetro elasticidade de substituição entre variedades.
pertencem ambos a uma acordo de integração regional que prevê livre circulação de
bens (para além de pessoas e serviços). Como tal  kl deveria ser igual a um. No entanto
Bröcker (1984) estima para os impedimentos aos fluxos inter-regionais de comércio
entre países da Comunidade Europeia, uma distância equivalente a 375 quilómetros.
Dado o valor para o custo da distância por unidade de distância (  =0.000046 por
quilómetro), este corresponde a um  kl de 1.19. Ou seja, uma tarifa equivalente de 19
porcento.
Pode-se pensar que este valor é demasiado elevado uma vez que os impedimentos
ao comércio quase desapareceram no mercado interno. No entanto considerando por
exemplo o Canadá e os EUA que também pertencem a um acordo de integração
regional (para além de culturas e língua muito semelhantes), McCallum (1995) estima
impedimentos ao comércio entre estes dois países superiores ao aqui considerados.
Seguindo o valor avançado no parágrafo anterior para  kl , o comércio intra-regiões do
mesmo país é 5.6 vezes superior ao comércio intra-regiões trans-fronteiriço. Se
considerarmos o estudo de McCallum, o comércio intra-regiões do Canadá é 22 vezes
superior ao comércio intra-regiões do Canadá e EUA. Tomando a elasticidade de
substituição por nós considerada (  =10) isto seria equivalente a uma tarifa equivalente
de 36 porcento. Como tal no presente estudo consideramos que este apenas é igual a um
quando duas regiões pertencem ao mesmo país. Se duas regiões pertencem a diferentes
países este parâmetro toma um valor superior a um, nomeadamente e como referimos
atrás uma tarifa equivalente de 19 porcento.
O parâmetro que resta (  r ) é calibrado, resolvendo um sistema de equações que
determina este parâmetro assim como todas as variáveis endógenas, dado o valor dos
parâmetros discutidos nos parágrafos anteriores. Este sistema de equações fixa  r de
modo a que na solução de equilíbrio, o PIB regional de uma região iguale o PIB
regional observado para esta mesma região.
Para derivar este sistema de equações considere-se inicialmente que Vr é conhecido
para todo o r . Já foi referido que t rs respeita as equações de um modelo gravitacional
com duas restrições (equação (13)) ou as equações (29), (30) e (31):
t rs  arVr bsVs f rs
(32)
Vs   t rs
r
(33)
Vr   t rs
s
(34)
com ar  pr e f rs   rs . Este sistema pode ser solucionado por “iterative scaling”
(Darroch and Ratcliff, 1972). Encontrando a solução para o sistema de equações (32),
(33) e (34), os multiplicadores a r , e bs também podem ser achados para um factor de
escala arbitrário. Portanto é também possível encontrar os preços p r (para um factor de
escala arbitrário) através da relação:

pr  ar
1

(35)
Achando p r é também possível através da equação (12) encontrar os preços do
bem compósito q s (novamente para um factor de escala arbitrário). De notar que o
factor de escala é fixado apenas para escolher unidades para o bem compósito e
produção.
É pois possível calcular o preço dos bens se os valores da produção forem
conhecidos. No entanto se conhecermos o preço dos bens também é possível achar os
valores de produção. Para isso é necessário fazer uma hipótese adicional. Assume-se
que o preço do capital ( z r ) é constante em todas as regiões. Esta hipótese pode ser
justificada se assumirmos que existe perfeita mobilidade do capital inter-regional, o que
pode de facto ser irrealista e muito discutível. Mesmo supondo que tal é verdade, apenas
é possível argumentar em favor de uma taxa de retorno igual nos activos
comercializáveis. A taxa real de retorno em capital instalado pode desviar-se da taxa
igualizada entre regiões, porque a instalação deste tipo de capital é muito onerosa e
rígida no tempo (Hayashi, 1982). No entanto pode-se argumentar que estes desvios
podem desaparecer no longo prazo24.
24
Bröcker (1998a) para além desta hipótese faz uma hipótese adicional. Ele supõe que a taxa de participação laboral é constante em
todas as regiões. Assim em Bröcker a força de trabalho regional (
Lr ) é proporcional à população ( Br ), o que significa que
Lr  Br , com taxa de participação  . Neste trabalho optou-se por seguir as condições do modelo
e utilizar dados em
emprego regional (em vez de dados para a população como em Bröcker, 1998a) para não ser necessário fazer hipóteses adicionais
(ver equação (16)).
Para uma região r obtém-se da equação (2):

 p q 
wr   r r
_
z 
r






1

(36)
_
onde z denota o preço constante do capital. Pode-se pois concluir da equação (16):
Vr 
Lr wr

(37)
Substituindo em (37) wr pelo seu valor em (36) obtêm-se:
1

V r   r Lr p r q r



(38)
1
com  r 

_

1
.
25
  z  r 


Neste momento estamos em condições de calibrar  r fazendo uso da
informação disponível quanto ao PIB regional ( Yr ). Como tal  r é calibrado (ou
melhor dizendo,  r é calibrado, que é função de  r e outras constantes), de modo a
que o PIB regional observado coincida com PIB regional do modelo. Isto vai implicar:
Yr     Vr
(39)
ou substituindo Vr pelo seu valor em (38):
1


Yr      r Lr p r q r 
(40)
Esta equação dá-nos  r e também Vr :
Vr 
Yr

(41)
_
25
Considera-se uma taxa de remuneração do capital,
z =0.05.
O procedimento de calibração resume-se de seguida. Inicia-se o processo com
pr  qr  1, r , e encontra-se Vr da equação (41). De seguida resolve-se as equações
(32), (33) e (34) por “iterative scaling” para se achar a matriz de comércio interregional t rs . Destes resultados calcula-se p r da equação (35) e q s da equação (12).
Caso se obtenha convergência pode dar-se por terminada a calibração, caso contrário,
reinicia-se o processo com os preços p r e q s da última iteração.
Em alternativa a este processo de calibração tem-se um outro. Recordemos as
equações (32), (33), e (34), como Vr   t rs , então:
s
t
rs
 a rVr  bsVs f rs   Vr  a rVr  bsVs f rs 
s
s
s
(42)
logo:
ar 
1
 bsVs f rs 
s
(43)
como ar  pr , obtem-se p r :
1


p r    bsVs f rs 
 s

(44)
Depois de se achar Vr por (41), fazendo p r0  q r0  1 , é possível achar b s0 de (28), p 1r
de (44) e q 1s de (12)26. Tendo estes faz-se iterações até se obter convergência em p r e
q s . No presente estudo optou-se por seguir este método de calibração.
6.
ACESSIBILIDADE NA PENÍNSULA IBÉRICA
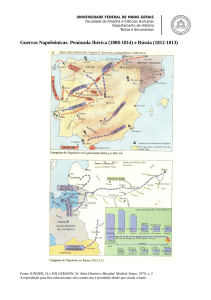
A figura 1 ilustra os resultados do indicador de acessibilidade definido na equação
(24), escalado para a unidade. As linhas unem localizações com o mesmo potencial de
mercado, enquanto que as setas sinalizam as regiões com maior acessibilidade
económica.
26
O super-escrito refere-se ao número da iteração.
Figura N.º 1 -
Linhas de Acessibilidade na Península Ibérica
A medida de acessibilidade para as regiões NUTS 2 de Portugal e Espanha também
é apresentada no quadro 2. O indicador de acessibilidade varia entre um mínimo de 0.60
na região do Algarve, e um máximo de 1.44 na região de Madrid. Como tal dada a
distribuição espacial dos mercados, uma firma representativa em Madrid pode pagar aos
factores de produção localizados nesta região, cerca de duas vezes e meia mais do que
pode pagar na região do Algarve, se a tecnologia usada nas duas localizações fosse
semelhante.
Quadro N.º 2 Acessibilidade e Bem-Estar
pr
qr
Fr
ur
Região
Galiza
Principado de Astúrias
Cantábria
Pais Vasco
Comunidade Foral de Navarra
La Rioja
Aragão
Comunidade de Madrid
Castela e Leão
Castilla-la Mancha
Estremadura
Catalunha
Comunidade Valenciana
Andaluzia
Múrcia
Norte
Centro (P)
Lisboa e Vale do Tejo
Alentejo
0.940432
0.951697
0.966559
0.978418
0.965164
0.975754
0.984214
1.013808
0.992065
0.996772
0.946212
1.002049
0.990754
0.975363
0.950343
0.932433
0.932861
0.941122
0.916811
1.020205
1.021203
1.086228
0.918034
1.058311
1.152813
0.997903
0.860459
0.940104
1.006399
1.059129
0.896896
0.924077
0.898903
1.049203
0.940527
1.008873
0.903521
1.127263
0.853028
1.0283
1.016717
1.316397
1.093967
0.953192
1.131997
1.436925
1.078134
1.050275
0.944973
1.339999
1.168141
1.195334
1.022066
0.682622
0.611749
0.870606
0.603366
0.828588
0.986605
0.971344
1.392303
1.255171
1.066941
1.226205
1.570936
1.077036
0.889544
0.731047
1.48743
1.106899
0.874651
0.894722
0.711675
0.634971
1.069736
0.553074
Algarve
0.873442 1.129949
0.60221 0.671122
Considere-se a Espanha e Portugal isoladamente. No primeiro caso a região com
menor acessibilidade é a região da Galiza, sendo Madrid a região com mais potencial de
mercado. No segundo caso a região com melhor acessibilidade é Lisboa enquanto que a
de pior grau da acessibilidade é o Algarve. De notar que no entanto Lisboa apesar de ser
a região de Portugal com melhor acessibilidade na Península Ibérica, esta apenas tem
uma acessibilidade marginalmente superior à da região menos central da Espanha (0.87
de Lisboa contra uns 0.85 da Galiza).
Para além do máximo global em Madrid, de destacar outros máximos locais à volta
das regiões da Catalunha (1.34) e País Vasco (1.32). A actividade económica na
Península Ibérica parece pois estar fortemente enviesada para três centros geográficos à
volta de Madrid, Catalunha e País Vasco.
O quadro 2 também apresenta os níveis regionais de utilidade tal como definido na
equação (8), escalada para uma média da unidade. A utilidade varia entre um máximo
de 1.57 em Madrid a um mínimo de 0.55 no Alentejo. No caso da Espanha a região
NUTS 2 com menor nível de utilidade é a região da Estremadura (0.73). Em Portugal a
região com maior utilidade é Lisboa (1.07).
7.
ANÁLISE DE SENSIBILIDADE
A calibração é criticada por várias razões. Em primeiro lugar a calibração é feita em
relação a um ano base em que se supõem que as condições de equilíbrio do modelo se
verificam na economia, o que como é óbvio é bastante irrealista pensar que tal ano
exista. Por outro lado temos o problema da escolha das equações do modelo para a
calibração. Desde logo se coloca a questão de quais as equações do modelo com mais
significado económico, uma vez que para diferentes escolhas podemos ter diferentes
valores dos parâmetros. Além disso muitas vezes tem que se escolher valores para
certos parâmetros (como por exemplo economias de escala), e estes devem ser obtidos
de preferência através de estudos econométricos. Por último e confrontando a
econometria e a calibração (apesar de todas as críticas que se podem apontar também à
primeira), na econometria utiliza-se métodos estocásticos, o que implica intervalos de
confiança para os parâmetros calculados, tal não é o caso na calibração. Deste modo na
calibração não se pode ter certeza da precisão dos valores conseguidos.
Sendo assim os resultados obtidos da calibração de modelos devem sempre ser
encarados com muita precaução. De facto estes modelos apesar de permitem quantificar
interacções entre variáveis, e a resposta da economia a alterações de política; não
permitem testar a teoria. Dados estes argumentos é muito aconselhável levar a cargo
testes de sensibilidade para se ter uma ideia da robustez dos resultados.
Com este objectivo em mente, o modelo foi re-calibrado para um parâmetro de
elasticidade de substituição de  = 5 e  =15. No primeiro caso o valor de 
corresponde a um parâmetro de distância de  = 0.00023, e no segundo caso um
 =0.00069. Deste modo com  =5 é considerada uma menor elasticidade de
substituição entre variedades, e um menor impacto da distância nas variáveis em causa
(ver quadro 3). Já com  =15 considera-se uma maior elasticidade de substituição entre
variedades, e um maior impacto da distância no potencial de mercado de uma região
(ver quadro 4).
Quadro N.º 3 -
Acessibilidade e Bem-Estar (  =5)
Regiões
Galiza
Principado de Astúrias
Cantábria
Pais Vasco
Comunidade Foral de Navarra
La Rioja
Aragão
Comunidade de Madrid
Castela e Leão
Castilla-la Mancha
Estremadura
Catalunha
Comunidade Valenciana
Andaluzia
Múrcia
Norte
Centro (P)
Lisboa e Vale do Tejo
Alentejo
Algarve
Quadro N.º 4 -
pr
0.897456
0.928076
0.946382
0.955444
0.951913
0.967164
0.978084
1.00453
0.985058
0.98942
0.937544
0.966948
0.974172
0.940395
0.935337
0.871808
0.87817
0.874898
0.871272
0.826636
qr
1.038561
1.008982
0.993061
0.98574
0.99017
0.972322
0.965186
0.933094
0.948396
0.945784
0.987161
0.993578
0.970972
0.992841
1.006174
1.044112
1.035288
1.040904
1.044369
1.103304
Fr
0.840016
1.052014
1.122204
1.232086
1.174112
1.140265
1.173157
1.333555
1.105641
1.122831
1.016747
1.207793
1.110462
1.081411
1.06522
0.612522
0.59401
0.752636
0.648852
0.614467
ur
0.818575
1.004237
1.06852
1.304051
1.349182
1.272195
1.274985
1.456895
1.073695
0.951941
0.788807
1.350334
1.059433
0.796402
0.938294
0.644719
0.622291
0.933832
0.60037
0.691242
Acessibilidade e Bem-Estar (  =15)
Regiões
Galiza
Principado de Astúrias
Cantábria
Pais Vasco
Comunidade Foral de Navarra
pr
0.973614
0.967577
0.976283
0.990609
0.970848
qr
1.006991
1.017192
1.003291
0.98861
1.007645
Fr
ur
0.868985 0.846287
1.046718 0.99855
1.114142 1.060192
1.232249 1.30342
1.157268 1.329001
La Rioja
Aragão
Comunidade de Madrid
Castela e Leão
Castilla-la Mancha
Estremadura
Catalunha
Comunidade Valenciana
Andaluzia
Múrcia
Norte
Centro (P)
Lisboa e Vale do Tejo
Alentejo
Algarve
0.97679
0.982454
1.016372
0.995426
0.998781
0.955669
1.007669
0.99575
0.994389
0.960661
0.976522
0.971855
0.983049
0.950752
0.912745
0.998274
0.989463
0.948345
0.975227
0.966138
1.018545
0.955797
0.975264
0.974271
1.02049
1.012464
1.015918
1.00132
1.036621
1.088136
1.114002
1.147831
1.316121
1.078469
1.102528
0.9884
1.259354
1.108927
1.105374
1.053467
0.633582
0.607171
0.784776
0.655707
0.624929
1.24213
1.24672
1.436945
1.046688
0.934148
0.766357
1.407117
1.057331
0.813551
0.927377
0.666485
0.635695
0.973103
0.606326
0.702578
Tal como ilustrado no quadro 3 (para  =5) e quadro 4 (para  =15) os resultados
obtidos anteriormente não se alteram consideravelmente. De facto é possível constatar
que não se verifica qualquer variação qualitativa nos resultados, a própria variação
quantitativa não é significativa.
Pode-se pois concluir que no que concerne ao parâmetro elasticidade de
substituição os resultados da calibração não demonstraram ser muito sensíveis.
8.
ALTERAÇÕES DE POLÍTICA
A alteração de política considerada nesta secção supõe um mercado Ibérico
totalmente integrado. Na prática isto equivale a fixar o parâmetro de impedimentos ao
comércio internacional (  kl ) igual a um para todas as regiões NUTS 2. O quadro 5
apresenta os resultados desta simulação.
Quadro N.º 5 -
Acessibilidade com Mercado Ibérico Integrado (  kl =1, r )
Regiões
Galiza
Principado de Astúrias
Cantábria
Pais Vasco
Comunidade Foral de Navarra
La Rioja
Aragão
Comunidade de Madrid
Castela e Leão
Castilla-la Mancha
Estremadura
Catalunha
Comunidade Valenciana
Andaluzia
Múrcia
Norte
pr
0.96693
0.967127
0.9791
0.990085
0.975864
0.987651
0.99387
1.028415
1.009861
1.012443
0.986254
1.007979
1.000017
1.000464
0.960992
0.983178
qr
1.025633
1.020983
1.00766
0.9971
1.009597
0.996715
0.989953
0.958217
0.97505
0.972991
1.000851
0.981039
0.986062
0.99095
1.02619
1.006632
Fr
0.855389
1.045477
1.112158
1.224864
1.15798
1.118597
1.150229
1.305891
1.081449
1.097576
1.008457
1.230091
1.099615
1.089567
1.050313
0.638891
ur
0.833021
0.997377
1.058286
1.295616
1.329812
1.247242
1.249279
1.425764
1.049546
0.929932
0.781893
1.374406
1.048418
0.801896
0.924575
0.672055
Centro (P)
Lisboa e Vale do Tejo
Alentejo
Algarve
0.983786 1.004836 0.615436 0.644344
0.98764 1.003775 0.784866 0.973198
0.984499 1.003987 0.678741 0.627629
0.950778 1.04178 0.654414 0.735711
Tal como na secção anterior a alteração no valor de um parâmetro não causou
alterações significativas nos resultados da calibração base: em geral as regiões
Espanholas são mais centrais que as regiões portuguesas; a acessibilidade atinge um
pico nas regiões de Madrid, Catalunha, e País Vasco; o potencial de mercado atinge os
valores mínimos nas regiões portuguesas.
Este exercício permite também avaliar a alteração no bem-estar das regiões
espanholas e portuguesas em consequência de uma integração total das duas economias.
Neste sentido foi calculado o indicador de bem-estar de Hicks de variação equivalente
relativa, tal como definido na equação (18)27. O quadro 6 apresenta os resultados.
Quadro N.º 6 -
Variação Equivalente Relativa (VER)
Regiões
VER
Galiza
-0.00532
Principado de Astúrias
-0.0108
Cantábria
-0.08215
Pais Vasco
0.074626
Comunidade Foral de Navarra -0.05613
La Rioja
-0.14456
Aragão
-0.01847
Comunidade de Madrid
0.10182
Castela e Leão
0.026192
Castilla-la Mancha
-0.04343
Estremadura
-0.06503
Catalunha
0.082235
Comunidade Valenciana
0.05578
Andaluzia
0.090728
Múrcia
-0.03229
Norte
0.058955
Centro (P)
-0.01455
Lisboa e Vale do Tejo
0.099197
Alentejo
-0.11879
Algarve
-0.08779
Da análise do quadro conclui-se que a maior parte das regiões tem uma perda de
bem-estar com o cenário de integração completa. As regiões de Rioja na Espanha e
Alentejo em Portugal são as regiões com as maiores perdas relativas (14% em Rioja, e
12% no Alentejo). Das vinte regiões NUTS 2 de Portugal e Espanha apenas oito regiões
27
O equilíbrio de referência usado na computação desta medida de bem-estar foi o calculado na secção 5. O equilíbrio contra-factual
considerado é o da presente secção.
conseguem obter ganhos de bem-estar. Curiosamente entre estas encontram-se as
regiões mais desenvolvidas e avançadas de ambos os países. No caso da Espanha
Madrid, País Vasco e Catalunha, e no caso de Portugal Lisboa e Norte28. Os ganhos
nestas regiões variam entre uns 10% em Madrid e uns 2.5% em Castela e Leão.
9.
DISCUSSÃO
Este trabalho apresenta uma metodologia para quantificar a acessibilidade
económica no contexto de um modelo de geografia económica. Ao contrário das
medidas tradicionais de potencial de mercado desenvolvidas de uma forma ad-hoc sem
uma estrutura teórica-económica sólida por de trás; a presente metodologia tem os seus
alicerces num modelo que explicita a estrutura de mercado, agentes e interacções
estratégicas.
Esta especificação para além deste benefício teórico tem outras vantagens. Em
primeiro lugar é possível confrontar os resultados do modelo com dados da economia
real, como fluxos de comércio. Na medida tradicional tal não era possível porque a
única relação testada era a acessibilidade, e esta não é observável. Em segundo lugar
cenários de política alternativos são simulados de uma forma natural no modelo
resolvendo para o novo equilíbrio, sem ter que desta forma recorrer a hipóteses
adicionais como acontecia na abordagem tradicional.
A aplicação do modelo apresentado neste trabalho ao caso da Península Ibérica,
permite tirar algumas conclusões prévias e não definitivas. Em primeiro lugar em
termos de centralidade a economia espanhola parece levar uma grande vantagem sobre a
economia portuguesa. De facto Portugal aparece neste estudo quase como uma
economia periférica da espanhola, onde nem sequer a região da capital portuguesa
(região mais desenvolvida de Portugal) consegue ter no conjunto da Península Ibérica
uma importância relevante em termos de potencial económico.
O pico de acessibilidade é atingido pela região de Madrid sendo seguida de perto
pelo País Vasco e pela Catalunha, formando estas três os principais centros económicos
da Península Ibérica. Estes resultados não se mostraram sensíveis a testes de
sensibilidade efectuados a alguns dos parâmetros.
28
De notar que a região Norte portuguesa não pode ser considerada no seu todo uma região desenvolvida. De facto é possível dividir
esta
em uma região Litoral desenvolvida, com uma elevada densidade populacional, e com um grande peso da industria
transformadora no total da actividade económica desta região; e uma região interior economicamente atrasada, com uma fraca
densidade populacional, onde predomina principalmente a actividade agrícola tradicional. Como tal a parte interior da região Norte
é mais similar à região do Alentejo do que à sua contraparte Litoral.
Em segundo lugar um cenário de integração completa entre a economia portuguesa
e a economia espanhola não aparenta ser benéfica para uma parte considerável das
regiões. Tal como previsto pela literatura na “nova” geografia económica as regiões
mais beneficiadas seriam as mais avançadas, evidenciando portanto efeitos de “lock-in”
e efeitos de casualidade cumulativa.
10. BIBLIOGRAFIA
Bröcker, J. (1984), “How do International Trade Barriers Affect Interregional
Trade”, in: A. Anderson; W. Isard e T. Pu (eds.), Regional and Industrial Development
Theories: Models and Empirical Evidence, Amsterdam: North Holland
Bröcker, J. (1989), “How to Eliminate Certain Defects of the Potential Formula”,
Environment and Planning, 21, pp. 817-830
Bröcker, J. (1998a), “Measuring Accessibility in a General Equilibrium
Framework”, in: A. Reggiani (ed.), Accessibility, Trade and Locational Behaviour,
Aldershot: Ashgate
Bröcker, J. (1998b), “How Would an EU-Membership of the Visegrád-Countries
Affect Europe’s Economic Geography”, The Annals of Regional Science, 32, pp. 91-114
Bröcker, J. (1998c), “Operational Spatial Computable General Equilibrium
Modeling”, The Annals of Regional Science, 32, pp. 367-387
Bröcker, J. e Jäger-Roschko, O. (1996), “Eastern Reforms, Trade and Spatial
Change in the EU”, Papers in Regional Science, 75, pp. 23-40
Bröcker, J. e Rohweder, H. (1990), “Barriers to International Trade: Methods of
Measurement and Empirical Evidence”, The Annals of Regional Science, 4, pp. 289-305
Clark, C.; Wilson, F. e Bradley, J. (1969), “Industrial Location and Economic
Potential in Western Europe”, Regional Studies, 3, pp. 197-212
Darroch, J. e Ratcliff, D. (1972), “Generalized Iterative Scaling for Log-Linear
Models”, Annals of Mathematical Statistics, 43, pp. 1470-1480
Davis, D. (1998), “The Home Market, Trade, and Industrial Structure”, The
American Economic Review, 88, pp. 1264-1276
Dixit, A. e Stiglitz, J. (1977), “Monopolistic Competition and Optimum Product
Diversity”, American Economic Review, 67, pp. 297-308
EUROSTAT (1996), “REGIO: Banque de Données Régionales, Description du
Contenu”, Luxembourg: Commission des Communautés Européennes
Flôres, R. (1997), “The Gains from MERCOSUL: A General Equilibrium,
Imperfect Competition Evaluation”, Journal of Policy Modelling, 19, pp. 1-18
Fujita, M; Krugman, P. e Venables, A. (1999), “The Spatial Economy: Cities,
Regions, and International Trade”, Cambridge: MIT Press
Fujita, M. e Thisse, J.-F. (1996), “Economics of Agglomeration”, CEPR Discussion
Paper, No.1344, February
Gasiorek, M.; Smith, A. e Venables, A. (1994), “Modelling the Effect of Central
and East European Trade on the European Community”, in: The Economic
Interpenetration Between the European Union and Eastern Europe, European Economy
No. 6, Report and Studies Part C, Chapter 3, Brussels: European Commission
Hanson, G. (1998), “Market Potential, Increasing Returns, and Geographic
Concentration”, NBER Working Paper, No. 6429, February
Harris, C. (1954), “The Market as a Factor in the Localization of Production”,
Annals of the Association of American Geographers, 44, pp.315-348
Hayashi, F. (1982), “Tobin’s Marginal q and Average q: a Neoclassical
Interpretation”, Econometrica, 50, pp. 213-224
Keeble, D.; Offord, J. e Walker, S. (1988), “Peripheral Regions in a Community of
Twelve Member States”, Luxembourg: Commission of the European Communities
Krugman, P. (1991), “Increasing Returns and Economic Geography”, Journal of
Political Economy, 99, pp. 413-499
Krugman, P. (1993), “On the Number and Location of Cities”, European Economic
Review, 37, pp. 293-298
McCallum, J. (1995), “National Boundaries Matter: Canada-US Regional Trade
Patterns”, American Economic Review, 85, pp. 615-623
Pires, A. J. G. (1999), “Distribuição Espacial da Actividade Económica na
Espanha: Estimação dos Parâmetros Estruturais de um Modelo de Geografia
Económica”, Tese de Mestrado, ISEG/UTL
Venables, A. (1996), “Equilibrium Locations of Vertically Linked Industries”
International Economic Review, 37, pp. 341-359
Vickerman, R. (1991), “Transport Infrastructure in the European Community: New
Developments, Regional Implications and Evaluation”, in: R. Vickerman (ed.),
Infrastructure and Regional Development, London: Pion