Lista de Exercícios

Lista de Exercícios
01. (UNICAMP 2007) Sensores de dimensões muitos pequenas têm sido
acoplados a circuitos micro-eletrônicos. Um exemplo é um medidor de
aceleração que consiste de uma massa m presa a uma micro-mola de

constante elástica k. Quando o conjunto é submetido a uma aceleração a , a

micro-mola se deforma, aplicando uma força Fel na massa (ver diagrama
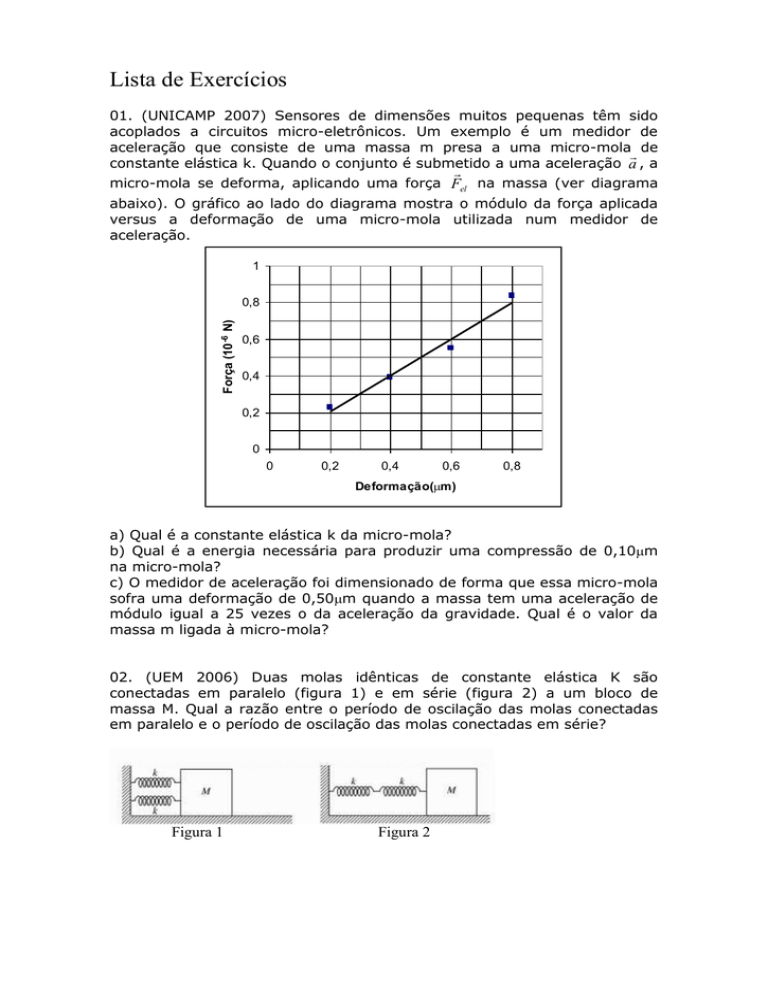
abaixo). O gráfico ao lado do diagrama mostra o módulo da força aplicada
versus a deformação de uma micro-mola utilizada num medidor de
aceleração.
1
Força (10 -6 N)
0,8
0,6
0,4
0,2
0
0
0,2
0,4
0,6
0,8
Deformação(m)
a) Qual é a constante elástica k da micro-mola?
b) Qual é a energia necessária para produzir uma compressão de 0,10m
na micro-mola?
c) O medidor de aceleração foi dimensionado de forma que essa micro-mola
sofra uma deformação de 0,50m quando a massa tem uma aceleração de
módulo igual a 25 vezes o da aceleração da gravidade. Qual é o valor da
massa m ligada à micro-mola?
02. (UEM 2006) Duas molas idênticas de constante elástica K são
conectadas em paralelo (figura 1) e em série (figura 2) a um bloco de
massa M. Qual a razão entre o período de oscilação das molas conectadas
em paralelo e o período de oscilação das molas conectadas em série?
Figura 1
Figura 2
03. (UFRGS 2003) Na figura abaixo estão representadas as configurações
espaciais instantâneas de duas ondas transversais senoidais, M e N, que se
propagam na direção x, ao longo de uma mesma corda musical.
Sendo M e N, respectivamente, o comprimento de onda e a freqüência da
onda M, é correto afirmar que o comprimento de onda N e a freqüência fN
da onda N são tais que
(A) N = 3M e fN=fM/3.
(B) N = 3M e fN=fM.
(C) N = M/3 e fN=3fM.
(D) N = M/3 e fN=fM/3.
(E) N = M e fN=3fM.
Justifique sua resposta.
04. (UFRGS 2003) As figuras abaixo ilustram um experimento muito
simples, que consiste em fazer um pulso transversal, que se propaga ao
longo de uma mola fina e muito longa, passar por uma fenda estreita.
As figuras (a), (b) e (c) procuram mostrar o seguinte:
(a) Se a direção do plano de oscilação do pulso for paralelo à fenda, o pulso
passa por ela.
(b) Se a direção do plano de oscilação do pulso for perpendicular à fenda, o
pulso não passa pela fenda e, em vez disso, reflete-se nela.
(c) Se a direção do plano de oscilação do pulso for oblíquo à fenda, o pulso
passará parcialmente por ela.
Pode-se afirmar que, nesse experimento, está sendo demonstrado o
fenômeno ondulatório da
(A) polarização.
(B) refração.
(C) difração.
(D) interferência.
(E) dispersão.
Justifique sua resposta.
05. (UNICAMP 2009) As medidas astronômicas desempenharam papel vital
para o avanço do conhecimento sobre o Universo. O astrônomo grego
Aristarco de Samos (310-230 a.C.) determinou a distância Terra-Sol e o
diâmetro do Sol. Ele verificou que o diâmetro do Sol é maior que o da Terra
e propôs que a Terra gira em torno do Sol.
a) Para determinar a distância Terra-Sol dS Aristarco mediu o ângulo 
formado entre o Sol e a Lua na situação mostrada na figura a seguir.
Sabendo-se que a luz leva 1,3s para percorrer a distância Terra-Lua dL, e
que medidas atuais fornecem um valor de  = 89,85º, calcule dS.
Dados:
Velocidade da luz: c = 3,0x108 m/s
cos(89,85°)=sen(0,15°)=2,6x10-3
06. (PUCRS 2005 inverno)
I. O campo magnético terrestre induz correntes elétricas na fuselagem de
alumínio de um avião que esteja voando.
II. Um ímã colocado dentro de um solenóide induz uma diferença de
potencial elétrico entre as extremidades deste solenóide, quer esteja
parado, quer em movimento em relação ao mesmo.
III. O fluxo magnético através de uma superfície é diretamente proporcional
ao número de linhas de indução que a atravessam.
IV. Um dínamo e um transformador são equipamentos projetados para
empregar a indução eletromagnética e por isso geram energia elétrica.
Analisando as afirmativas, conclui-se que somente estão corretas:
A) I, II e III.
B) I, II e IV.
C) II, III e IV.
D) I e III.
E) II e IV.
07. (UFRGS 2002) A histórica experiência de Oersted, que unificou a
eletricidade e o magnetismo, pode ser realizada por qualquer pessoa,
bastando para tal que ela disponha de uma pilha comum de lanterna, de um
fio elétrico e de:
(A) um reostato.
(B) um eletroscópio.
(C) um capacitor.
(D) uma lâmpada.
(E) uma bússola.
08. (ENADE 2005)
Diversos sistemas físicos amortecidos encontrados em engenharia podem
ter seu comportamento expresso por meio de equações diferenciais
ordinárias não-homogêneas de segunda ordem. A resolução desse tipo de
equação envolve a obtenção da resposta yh(t) da equação diferencial
homogênea associada, que expressa o comportamento do sistema livre de
excitações externas, e a obtenção de uma solução particular yp(t) da
equação não-homogênea. A soma de yp(t) e yh(t) fornece a solução geral da
equação não-homogênea. A resposta livre permite identificar a freqüência
das oscilações amortecidas (f) e a constante de amortecimento (k) do
sistema. Considere que a resposta livre de um sistema seja dada pela
função
yh(t) = 5e-k t cos(2  f t),
cujo gráfico está ilustrado na figura a seguir.
A freqüência das oscilações amortecidas do sistema cuja resposta livre está
apresentada no texto é igual a:
(A) 0,1Hz.
(B) 0,15Hz.
(C)  rad/s.
(D) 10 rad/s.
(E) 10Hz.
Justifique sua resposta.
09. ( adaptado ENADE 2008)
Alguns tipos de balança utilizam, em seu funcionamento, a relação entre o
peso P e a deformação elástica  que ele provoca em uma mola de
constante elástica K, ou seja, P = K x  (Lei de Hooke). Ao se colocar certa
mercadoria no prato de uma balança desse tipo, a deformação  não ocorre
instantaneamente. Existe um movimento transiente que depende de outro
parâmetro: o nível de amortecimento no mecanismo da balança, dado pelo
parâmetro adimensional , denominado fator de amortecimento.
O movimento transiente, a partir do instante em que a mercadoria é
colocada no prato da balança, pode ser descrito por 3 equações diferentes
(e tem comportamentos diferentes), conforme o valor de .
Com base nessas informações e nos dados abaixo, encontre a solução para
(t) na qual a balança indica o valor da massa mais rapidamente (=1).
Dados: m = 1kg, K= 100N/m, g=9,86m/s2
10. ( adaptado ENADE 2008)

Uma barra metálica é puxada de modo a deslocar-se, com velocidade v ,
sobre dois trilhos paralelos e condutores, separados por uma distância
como mostra a figura abaixo.
ℓ
,
Um resistor de resistência elétrica R conecta os dois trilhos, e um campo

magnético uniforme B atravessa, perpendicularmente, o plano do conjunto,
preenchendo todo o espaço. Qual é a intensidade da corrente elétrica que
atravessa o resistor?
11. (UEM 2007) Considere a figura abaixo, na qual são representadas três
ondas distintas. O deslocamento, na horizontal, se dá em 2,0 s, percorrendo
12,0 m.
Calcule, a partir das informações constantes no gráfico,
a) a amplitude de C;
b) o período de A;
c) a velocidade de B.
12. (adaptado UEM 2009) Considere uma onda mecânica que se propaga
em uma corda homogênea de acordo com a função horária
y(x,t) = 2 cos(2π(2t - 4x)) , para x e y dados em centímetros e t dado em
segundos, determine:
A) A amplitude da onda.
B) O comprimento de onda desta onda.
C) O período de oscilação da onda.
D) A velocidade de propagação da onda no meio.
E) Se a onda que se propaga nesta corda é progressiva ou regressiva.
13. MHS da balança de um açougue. Uma mola de massa desprezível e
constante K=400N/m está suspensa verticalmente e um prato de 0,200kg
está suspenso em sua extremidade inferior. Um açougueiro deixa cair sobre
o prato de uma altura de 0,40m uma posta de carne de carne de 2,2kg. A
posta de carne produz uma colisão totalmente inelástica com o prato e faz o
sistema executar um MHS. Calcule:
A) A velocidade do prato e da carne logo após a colisão;
B) A amplitude da oscilação subseqüente;
C) O período do movimento.
14. Uma partícula desloca-se num círculo no plano xy com centro na
origem. O raio do círculo é 40cm e a velocidade escalar da partícula
80cm/s.
A) Qual a velocidade angular da partícula;
B) Qual é a freqüência e o período do movimento circular;
C) Escrever as componentes do vetor posição r em função do tempo.
15. Um corpo de 3kg está preso a uma mola e oscila com amplitude de
10cm e a freqüência f=2Hz.
A) Qual é a constante de força (elástica) da mola;
B) Qual é a energia total do movimento;
C) Escrever uma equação x(t) que descreva a posição do corpo em relação
à sua posição de equilíbrio. A constante de fase pode ser determinada com
as informações fornecidas no problema?
16. Uma partícula oscila com movimento harmônico simples de período
T=2s. Inicialmente, está na posição de equilíbrio e se desloca com a
velocidade escalar de 4m/s, no sentido dos x crescentes. Escrever as
expressões da sua posição x, da sua velocidade v e da sua aceleração a em
função do tempo.
17.
A
função
de
onda
de uma onda harmônica numa corda é
yx, t   0,001sen62,8x  314t  , onde y e x estão em metros e t em segundos.
A) Em que direção esta onda se desloca e com qual velocidade;
B) Calcular o comprimento de onda, a freqüência e o período desta onda;
C) Qual é o deslocamento máximo de qualquer segmento da corda?
18. Uma corda, de 3m de comprimento, está fixa pelas duas extremidades.
A corda ressoa no segundo harmônico com freqüência de 60Hz. Qual é a
velocidade das ondas transversais na corda?
19. A função de onda de uma certa onda estacionária, numa corda fixa nas
duas extremidades, é yx, t   0,5 sen0,025xcos500t  , onde y e x estão em
centímetros e t em segundos.
A) Calcular a velocidade e a amplitude das duas ondas caminhantes que
provocam a onda estacionária;
B) Qual a distância entre os nós sucessivos na corda?
C) Qual é o menor comprimento possível da corda?
20. A fala humana normal provoca um nível de intensidade sonora de cerca
de 65dB a 1m de distância. Estimar a potência da fala.
Bibliografia Básica
HALLIDAY, D.; RESNICK, R.; WALKER,J. Fundamentos de Física - Vol.1, 2, 3,
4, 7ª Edição, LTC Editora . Rio de Janeiro, 2007.
TIPLER, P. A.; MOSCA,G. Física para Cientistas e Engenheiros, Vol, 1, 2 e 3.
5ª Edição , LTC Editora . Rio de Janeiro 2006