ROBERT WAYNE SAMOHYL,

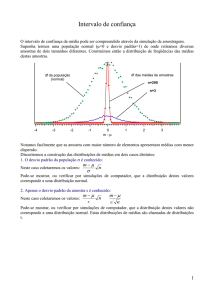
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de
qualidade (CEQ): variáveis mensuráveis
3.1 Introdução
3.2 Distribuição normal
3.2.1 Distribuições não-normais transformáveis em normal
3.2.2 Características matemáticas da distribuição normal: a relação entre o desvio
padrão da variável e a probabilidade
3.2.3 Distribuição normal padronizada (Z)
3.2.4 Exemplo na universidade: prêmio para os melhores alunos
3.2.5 Outros exemplos
3.3 Distribuição t (Gosset)
3.4 Algumas considerações sobre as distribuições F e χ2 (Chi quadrado)
3.5 Exercícios:
3.6 Referências
3.1 Introdução
O conceito de distribuição de freqüências e probabilidades de variáveis (ou mensuráveis
ou atributos), e principalmente o formato da distribuição, é central para a utilização de
estatística aplicada na melhoria de quaisquer processos produtivos. A tendência central
dos dados, a sua dispersão e assimetria são características que definem as distribuições,
e facilitam a análise e a inspiração das propostas para melhorias. O propósito desse
capítulo é formalizar e generalizar as definições dessas características distribucionais
para as variáveis mensuráveis (em matemática, contínuas) e utilizá-las nas ferramentas
de controle estatístico de qualidade. No capítulo seguinte vamos ver distribuições de
probabilidade para as variáveis discretas na área de controle estatístico de qualidade
chamadas atributos.
3.2 Distribuição normal
Como já foi discutido no capítulo 2 sobre as medidas descritivas e os gráficos básicos,
os dados que vem da distribuição normal produz um agrupamento de valores
observados próximos à média, e freqüências menores quando nos afastamos da média.
Esse formato é facilmente visto no histograma. A distribuição normal é simétrica e as
caudas são cada vez mais finas se distanciando da média1. Esse tipo de comportamento
das freqüências é surpreendentemente comum na realidade, em situações bem
diferentes, por exemplo, nas mensurações da linha de produção até em áreas tão
1
O formato da cauda de uma distribuição amostral pode ser calculado e comparado com o formato da
distribuição normal teórica. O coeficiente de assimetria e o de curtose que medem a distorção presente na
distribuição observada em comparação com valores teóricos da distribuição normal serão discutidos em
mais detalhes no capítulo 6 sobre teste de hipótese.
1
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
díspares como economia e biologia. Embora existam outras características relevantes
para uma definição matematicamente rigorosa da distribuição normal, a simetria e as
caudas finas são as mais importantes nas aplicações fabris do dia a dia.
Teoricamente, uma das regras básicas para a distribuição normal e, por sinal, para
qualquer distribuição de probabilidades, é que o total da área embaixo da curva é igual a
1,00. Já vimos essa regra na prática no histograma que tem sempre a soma das
freqüências percentuais igual a 100%. Outra regra é que os valores observados da
variável na distribuição normal poderiam pelo menos em teoria variar entre valores
infinitos, ambos positivos e negativos. Quer dizer, na prática os valores devem variar
livremente sem esbarrar em limites como zero ou um. Veja que, segundo esta regra,
uma amostra de percentagens não é distribuída normalmente, pois a percentagem não
pode ser menor que zero (0,00) nem maior que um (1,00).
3.2.1 Distribuições não-normais transformáveis em normal
Em alguns casos, ainda raros, dado o tipo de variável sob investigação, o pesquisador
não deve esperar a distribuição normal. O variável tempo (duração de tempo entre
eventos), por exemplo, quase nunca é distribuída normalmente. Veja o histograma na
figura 3.1 - A distribuição de tempos de parada de máquina esperando manutenção.
Freqüência
500
400
300
200
100
0
303
265
227
190
152
114
76
39
1
Minutos de parada da máquina
Figura 3.1 – A distribuição de tempos de parada de máquina esperando manutenção.
A freqüência total é de mil paradas de máquina.2 A distribuição mostra que na maioria
dos casos a parada é rápida, porém algumas são muito mais demoradas. É uma
característica comum que pode ser observada em fábricas, filas do banco ou paradas de
ônibus. A tendência central pode ser relativamente pequena, mas quase sempre ocorrem
2
Dados disponíveis do autor.
2
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
tempos mais longos forçando a cauda direita a ficar mais esticada, representando uma
assimetria exagerada.
Para resolver o problema de não normalidade, o pesquisador pode experimentar uma
transformação do dado original para um dado distribuído normalmente. Para dados de
tempo, a experiência diz que uma transformação logarítmica é a melhor sugestão inicial,
W = ln(X). Assim, transformando todos os dados da variável X pelo logaritmo natural e
montando o histograma dos dados transformados (ln(X)), veja na figura 3.2, fica
convincente que o resultado é a distribuição normal.
A transformação de Box Cox proporciona a transformação ótima para dada variável não
normal. É uma equação genérica e no computador é um algoritmo.3 A equação na forma
simplificada é
W = Xiλ
O valor de λ é escolhido entre 3 e -3 para resolver o problema da não normalidade da
variável. A idéia é muito simples: deve existir algum valor para λ que transforma a
variável original de não-normal em normal.
A forma matematicamente mais completa da transformação de Box-Cox segue a
equação
λ
X
i -1
X
(
λ
)=
i
λ
Em termos práticos, a equação é a mesma, mas existe um caso diferente, quando λ é
muito próximo ao zero. Quando λ não é muito próximo ao zero, as duas transformações
são essencialmente iguais e isso significa que a primeira transformação, por ser mais
simples, deve ser a preferida. No entanto, quando λ se aproxima ao zero, a
transformação mais completa é preferida, pois esse valor de zero significa que a
transformação correta seria do logaritmo natural (ln(Xi)). Nosso exemplo em cima dos
tempos de parada de máquina é desse tipo de caso, onde o logaritmo natural normaliza a
variável. A transformação de Box-Cox aparece em vários lugares nesse livro: em
capitulo 6 sobre teste de hipótese junto com o teste de normalidade de Bera-Jarque, em
capítulo 11 sobre o índice de capacidade, e em capítulo 12 sobre correlação para
garantir normalidade e para identificar a melhor relação linear entre duas variáveis. 4
A distribuição normal tem características matemáticas e práticas de fácil manuseio pelo
usuário e a sua utilização é preferível quando comparada com outras distribuições de
probabilidade. Com a variável transformada a normalidade, a análise estatística segue
sem maiores complicações e se for necessário os resultados são re-transformados para
seus valores e unidades originais.
3
Outras transformações existem na literatura, mas a transformação de Box-Cox é a mais utilizada nas
aplicações industriais.
4
Capítulo 6 terá mais detalhes sobre a transformação de Box-Cox, no entanto vale a pena relatar que o
valor de λ que melhor transforma a variável parada de máquina para normalidade é 0,026, muito próximo
ao zero e conseqüentemente indicando a transformação pelo logaritmo.
3
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Robert Wayne Samohyl, Ph.D.
Freqüência
Controle Estatístico de Qualidade (CEQ):
Minutos transformados
Figura 3.2 – A distribuição de tempos de parada de máquina após a aplicação da
transformação exponencial ln(X)
A comprovação de não normalidade e a transformação de variáveis para normalidade é
uma etapa muito importante para a análise correta de processos industriais, mas é
comum ignorar a verificação de normalidade, e conseqüentemente decisões são tomadas
baseadas em informações questionáveis e resultados subótimos.
3.2.2 Características matemáticas da distribuição normal: a relação entre o desvio
padrão da variável e a probabilidade
Nas figuras 3.3 (a, b, c, d), a distribuição normal é representada como a famosa curva de
sino. É o desenho dos dados e das respectivas freqüências gerados pela função teórica
da distribuição normal. São histogramas como antes com o refinamento de utilizar
dados teóricos, não reais. No entanto, desde que o mundo real tende a se representar
como a distribuição normal, as figuras a seguir ajudam a compreender melhor a
realidade e também a conveniência prática da distribuição normal.
4
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
Distribuição normal em desvio padrão
68,27%
15,865 %
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
Figura 3.3a - A distribuição normal em termos de um desvio padrão.
Quando analisamos a curva em termos do desvio padrão, podemos ver que ela tem
características estatísticas que facilita diagnósticos de grandes populações de dados;
diagnósticos que seriam impossíveis se a curva não existisse. O eixo horizontal das
figuras 3.3 é a escala de unidades convertidas em desvios padrão, das unidades
originais, por exemplo, peso de sacos de leite ou metros de comprimento. Na figura
3.3a, a área embaixo da curva entre um e menos um desvio padrão é igual a 0,6827,
quer dizer, 68,27% de toda a área embaixo da curva. Engenheiros gostam de falar em
682.700 partes por milhão (PPM). Isso significa que aproximadamente 2/3 dos dados
observados num histograma devem teoricamente cair entre um desvio padrão da média.
No exemplo do histograma dos sacos de leite no capítulo 2 (figura 2.4 e tabela 2.5) pode
conferir que 100 sacos de leite caem nessa categoria, considerando que o desvio padrão
é igual a 50 ml (e média igual a 1000 ml), e 100 sacos é 2/3 da amostra total de 150.
Ademais, a percentagem representa uma probabilidade: selecionando um único saco de
leite, a probabilidade é 68,27% de que o saco contém entre 950 ml e 1050 ml (a média
de 1000 ml mais e menos o desvio padrão de 50 ml). A soma da área das duas caudas é
chamada α, a área em cada cauda α/2, e a área dentro dos limites que não inclui as
caudas (1- α).5
Como regra, a área embaixo da curva de sino é sempre constante para determinada
distância em desvios padrão da média. Quando o caso for 2 desvios padrão, a figura
3.3b, a área embaixo da curva será 95,45%. Podemos raciocinar então que quase 5% da
amostra ficarão fora dos limites de dois desvios padrões, nas caudas finas da
5
Existe outra expressão muito utilizada na análise de gráficos de controle, o número médio de amostras
(NMA) tiradas em seqüência até acontecer um valor da amostra fora dos limites definidos (NMA = 1/ α).
No exemplo, NMA = 1/ α = 1/0,6827 ≈ 3 (aproximadamente). Esse conceito será revisto no capítulo 7, na
introdução a teoria básica de gráficos de controle.
5
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
distribuição (exatamente 2,275% em cada cauda). Aliás, segundo o raciocínio, um valor
de pouco menos que dois desvios padrão (1,96) dariam uma área embaixo da curva
igual a exatamente 95%. Esse valor de 1,96 desvios padrão é muito importante em
pesquisas práticas como vamos ver neste capítulo e capítulos futuros.
Distribuição normal em desvio padrão
95,45%
2,275%
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
Figura 3.3b - A distribuição normal em termos de dois desvios padrão.
Nas engenharias um ponto de referência para estudos de qualidade é três desvios padrão
do alvo do processo, chamado de limite natural do processo. A área nas caudas fora dos
dois limites de três desvios padrão é apenas 27/10.000 (para a soma das duas caudas) ou
em termos percentuais são 0,27%, praticamente somente um quarto de um por cento
(2700 PPM = 1/370)6. Quando um processo é capaz, os limites de especificação do
processo (tolerâncias) estão dentro dos limites naturais. Tradicionalmente, para ser
considerado um processo capaz, na linha de produção não deve rejeitar mais que 27
itens em cada 10.000 itens produzidos. Essa condição garante que apenas um mínimo de
características ficará fora das especificações e, portanto, não serão rejeitadas ou
retrabalhadas. Os benefícios em termos de custos reduzidos na fábrica são óbvios.
Vamos ver mais tarde, no capítulo 4 sobre gráficos de controle que neste caso o índice
de capacidade, muito utilizado na indústria brasileira, é igual a um.
6
Os ingleses gostam de usar como ponto de referência 3,09 desvios padrão. A probabilidade
correspondente é 99,9%, e a área em uma cauda é 0,1%. A taxa de rejeição considerando as duas caudas é
0,2% ou 1/500. Talvez os ingleses tenham razão em achar mais fácil trabalhar com 1/500 = 2000 PPM do
que 1/370 = 2700 PPM?
6
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
Distribuição normal em desvio padrão
99,73%
0,135%
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
Figura 3.3c - A distribuição normal em termos de três desvios padrão.
Uma nova meta da indústria moderna é ter limites de especificação em seis desvios
padrão do alvo do processo. É a famosa meta de seis sigmas 7. Seguindo a lógica até
agora desenvolvida sobre o desvio padrão e a área em baixo da curva da distribuição
normal, apresentamos a figura 3.3d. Apenas duas peças em cada bilhão de peças
fabricadas são não conformes quando as especificações ficam aos seis desvios padrões
do alvo. É uma meta praticamente impossível para alcançar8. É equivalente a encontrar
apenas dois erros de digitação numa biblioteca de 20.000 livros. Neste caso, o índice de
capacidade é igual a 2,00. Se forem encontrados na sua fábrica índices de capacidade
aproximando-se a esses valores, sua operação alcança níveis de eficiência considerados
de classe mundial na comunidade empresarial internacional. Por outro lado, é provável
que o índice de capacidade foi calculado numa maneira errada, e a única sugestão
possível é tentar entender melhor o conceito de capacidade e refazer os cálculos. Às
vezes índices de capacidade ficam extremamente altos em função de limites de
especificação desatualizados e frouxos demais. Se o índice for realmente igual a dois
mesmo, então parabéns, pois a sua fábrica está funcionando igual às melhores do
mundo.
Sigma (σ) é o símbolo grego para o desvio padrão, utilizado pelos estatísticos.
Todas as discussões a cerca de valores em torno de um bilhão certamente não tem valor na prática.
Quase não existe fábrica com produção que alcança a um bilhão de itens e assim falar em uma ou duas
pecas defeituosas nesta produção toda seria apenas uma constatação teórica, uma conjectura duvidosa.
7
8
7
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
Distribuição normal em desvios padrão
0,999999998
0,000000001
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
Figura 3.3d - A distribuição normal em termos de seis desvios padrão.
Deve ser claro que as figuras 3.3 ilustram a relação entre a área embaixo da curva para
determinados valores (1, 2, 3, 6) da distancia medida em desvios padrão da média, no
entanto, qualquer valor fracionário para os desvios padrão é aceitável para o cálculo da
área. Neste sentido, foi montada a tabela 3.1. Por exemplo, localizando o valor na tabela
para -1,50, o valor correspondente da área a esquerda deste valor é 0,067. Em outras
palavras, a área da cauda a esquerda de -1,50 é 6,7% de toda a área. A percentagem
responde a questão: qual é a probabilidade de encontrar valores menores que -1,5;
resposta é 6,7%.
Zi
-6
-5,9
-5,8
-5,7
-5,6
-5,5
-5,4
-5,3
-5,2
-5,1
-5
-4,9
-4,8
-4,7
-4,6
-4,5
-4,4
-4,3
-4,2
-4,1
-4
Area
acumulada
a esquerda
0,000000001
0,000000002
0,000000003
0,000000006
0,000000011
0,000000019
0,000000033
0,000000058
0,000000100
0,000000170
0,000000287
0,000000479
0,000000793
0,000001301
0,000002112
0,000003398
0,000005413
0,000008540
0,000013346
0,000020658
0,000031671
Zi
-3,9
-3,8
-3,7
-3,6
-3,5
-3,4
-3,3
-3,2
-3,1
-3,0
-2,9
-2,8
-2,7
-2,6
-2,5
-2,4
-2,3
-2,2
-2,1
-2,0
Area
acumulada
a esquerda
0,000048096
0,000072348
0,000107800
0,000159109
0,000232629
0,000336929
0,000483424
0,000687138
0,000967603
0,001349898
0,001865813
0,002555130
0,003466974
0,004661188
0,006209665
0,008197536
0,010724110
0,013903448
0,017864421
0,022750132
Zi
-1,9
-1,8
-1,7
-1,6
-1,5
-1,4
-1,3
-1,2
-1,1
-1
-0,9
-0,8
-0,7
-0,6
-0,5
-0,4
-0,3
-0,2
-0,1
Area
acumulada
a esquerda
0,02871656
0,035930319
0,044565463
0,054799292
0,066807201
0,080756659
0,096800485
0,11506967
0,135666061
0,158655254
0,184060125
0,211855399
0,241963652
0,274253118
0,308537539
0,344578258
0,382088578
0,420740291
0,460172163
Zi
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
Area
acumulada
a esquerda
0,5
0,539827837
0,579259709
0,617911422
0,655421742
0,691462461
0,725746882
0,758036348
0,788144601
0,815939875
0,841344746
0,864333939
0,88493033
0,903199515
0,919243341
0,933192799
0,945200708
0,955434537
0,964069681
0,97128344
Zi
2
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
Area
acumulada
a esquerda
0,97725
0,982136
0,986097
0,989276
0,991802
0,99379
0,995339
0,996533
0,997445
0,998134
0,99865
0,999032
0,999313
0,999517
0,999663
0,999767
0,999841
0,999892
0,999928
0,999952
Zi
4
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6
Area
acumulada
a esquerda
0,999968329
0,999979342
0,999986654
0,99999146
0,999994587
0,999996602
0,999997888
0,999998699
0,999999207
0,999999521
0,999999713
0,999999830
0,999999900
0,999999942
0,999999967
0,999999981
0,999999989
0,999999994
0,999999997
0,999999998
0,999999999
8
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
Tabela 3.1 – Valores de Zi e a área acumulada, a probabilidade de Zi ser menor.
A curva em forma de equação que relaciona X e Y nas figuras 3.3 é a famosa função da
distribuição normal, também chamada de gaussiana. A sua derivação não será
demonstrado aqui. A equação na forma com e sem logaritmos é colocada aqui somente
para a apreciação dos alunos. É considerado um dos avanços mais importantes de toda a
história da matemática quando foi descoberta pelo Francês radicalizado Inglês Abraham
De Moivre no início do século 18 e mais tarde, na virada para o século 19, utilizada na
prática e popularizada na área de cartografia pelo Alemão Carl Friedrich Gauss. Assim,
ficou com o nome “gaussiana”.
Yi  f ( xi ) 
ln Yi   ln ( x
1
 x 2
-
( xi -  x ) 2
e
2 x 2
( xi  x ) 2
2 ) 
2 x2
(x i  x ) 2
ln Yi   ln(2,507x ) 
22x
Os símbolos representam o seguinte: X = média, X = desvio padrão, e = 2,718,  =
3,142. A segunda equação é escrita em forma de logaritmos naturais.
3.2.3 Distribuição normal padronizada (Z)
Nas figuras 3.3 em cima, poderíamos definir o eixo horizontal em unidades originais da
variável original Xi, em medidas como centímetros, litros, reais ou dólares, ou como foi
feito na exposição das figuras, em termos de número ou fração de desvios padrão de
distância da média. O desvio padrão é a medida predileta do estatístico por causa da
relação matemática entre a distância da média em desvios padrão e as áreas
(probabilidades) fixas embaixo da curva da distribuição normal. Como será ilustrada em
um exemplo na próxima seção, a área embaixo da curva vai ajudar o pesquisador
solucionar problemas envolvendo grandes populações de dados. Muitas vezes a área da
cauda definida por algum valor crítico de Xi é essencial para chegar a reconhecer
através de amostragem características importantes da população, sem a necessidade de
analisar toda a população, mas sim somente uma pequena amostra. A área embaixo da
curva nas caudas definida por um valor crítico é chamada de P(Z), onde Z é a distancia
da média medida em desvio padrão. Quando a distribuição normal é padronizada com a
média igual a zero e desvio padrão unitária, como nas figuras 3.3, as percentagens de
área embaixo da curva podem ser avaliadas e tabeladas para qualquer número ou fração
de desvios padrão como foi feito na tabela 3.19. Nesse sentido, qualquer número Xi em
medidas originais como centímetros, litros, reais ou dólares pode ser transformado em
9
A formula da distribuição normal padronizada se simplifica à expressão: lnYi = - 0,919 – (Zi)2/2
9
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
variável padronizada Zi.10 A transformação entre Zi e Xi é uma expressão muito simples.
Primeiro, a média dos dados é calculada e o valor de Xi é subtraído resultando na
distância de Xi da média, o qual no capítulo 2 foi chamado de desvio ao redor da média.
Vamos ver um exemplo. Voltando para tabela 2.2, a média X das demoras para resolver
os problemas dos clientes é 182,89 minutos e, para ilustrar a transformação, vamos
escolher o oitavo número da lista, 325,89 minutos. A diferença entre os dois números (o
desvio a partir da média) é
325,89 – 182,89 = 143 minutos.
Então, para converter a medida original minutos em número de desvios padrão de
distância da média, é só dividir pelo valor do desvio padrão (94,99). Assim, podemos
escrever
Zi 
Xi  X
143
= 1,50 desvios padrão

desvio padrão 94,99
É comum na indústria considerar uma diferença de 1,5 desvios padrão da média como
aceitável para dados individuais. Considerando a variabilidade grande da série em 94,99
minutos, o resultado de atendimento do cliente em 325 minutos não é uma aberração
individual muito grande. Como foi exemplificado nas figuras 3.3, a área embaixo da
curva a direita de Zi (1,50) é a probabilidade P(Zi) de encontrar valores maiores que Xi
(325). A probabilidade foi encontrada na tabela 3.1 e é quase 7% (1 – 0,933). Muito
provavelmente o gerente tentando investigar esse valor para alguma causa especial não
vai encontrar nada. Se forem consideradas as duas caudas, a probabilidade é 14% de
encontrar valores pelo menos 1,50 desvios padrão da média em circunstâncias
perfeitamente normais com a média do processo estável e a variabilidade embora
grande, mas também estável. Aberrações individuais de 1,5 desvios padrão não são
grandes o suficiente para serem marcadas como especiais, e provavelmente não há
causas específicas atuando no processo. O problema nesse processo é com a dispersão
dos dados em geral. Se for considerada muito alta a dispersão deste processo pela
engenharia, para diminuir o desvio padrão do processo de atendimento ao cliente o
gerente terá que investigar todo o processo, procurando por causas comuns da
variabilidade atuando em todos os dados da série. Talvez seja necessário treinar o
pessoal e organizar melhor todo o processo de atendimento ao cliente.
É melhor e mais eficaz investigar o processo afetado por causas especiais quando
valores individuais de Xi resultaram em caudas bem menores que 1%. Como foi
ilustrado nas figuras 3.3, um ponto de referência para engenharia é universalmente
aceito para Zi = 3,00 e área da cauda P(Zi) = 0,135%. Vamos falar muito mais sobre
causas comuns e especiais na segunda parte do livro sobre gráficos de controle.
3.2.4 Exemplo na universidade: prêmio para os melhores alunos
Vamos ver agora, com um exemplo, como a distribuição normal padronizada pode ser
utilizada para analisar grandes populações de dados em uma maneira eficiente e rápida.
10
A distribuição padronizada também leva o nome de reduzida ou tabelada, dependendo do texto e do
autor, mas “padronizada” é hoje em dia mais comum, mais moderno.
10
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
De inferir informação sobre grande população (grande demais para serem pesquisados
todos os seus elementos) através da utilização de uma amostra aleatória é um dos
trabalhos mais importantes da área de estatística. Como será visto mais tarde, boa parte
da Estatística aplicada em ambientes empresariais aproveitam dos princípios
tradicionais da área de Estatística inferencial.
O exemplo que segue vem de uma idéia comum no ambiente empresarial. Qual é o
divisor das águas entre clientes especiais e os outros não tão especiais? Alguns bancos
já tentam determinar esse valor para montar a Sala VIP atraindo clientes ricos e
rentáveis para o banco com privilégios exclusivos e recintos requintados.
Uma grande universidade no sul do Brasil tem 18.000 alunos, uma população grande.
Imediatamente depois de cada semestre, o reitor gostaria apresentar um prêmio aos
melhores alunos com médias finais mais altas, mas o problema é como reconhecer
rapidamente esses alunos sem pesquisar todos os 18.000. É reconhecido que a
administração da universidade é lenta e leva mais ou menos um mês para processar as
médias finais da população de todas as disciplinas e alunos. O reitor alocou recursos
orçamentários suficientes para premiar mais ou menos 1% dos alunos (1% de 18000 é
180). Cada aluno será premiado com uma medalha de ouro e R$3.000,00.
Em primeiro lugar, temos que tirar uma amostra de 200 alunos representativa da
população de 18.000. Veja mais sobre amostragem no final desse capítulo. Nessa
amostra a média das avaliações dos alunos é 7,0 e o desvio padrão é igual a 1,0. Deve
existir um valor crítico da média das avaliações dividindo os 180 melhores alunos dos
demais. Utilizando conhecimentos sobre a distribuição normal padronizada, é possível
encontrar o valor crítico da média das avaliações que divide os alunos em dois grupos,
os melhores (premiáveis) e o resto. Trabalhando com os números da amostra, podemos
definir o valor da avaliação critica. O valor da área embaixo da curva P(Z) que interessa
é igual a 1%. É a área da cauda direita da distribuição normal padronizada onde se situa
as médias mais altas. (Por outro lado, se for desejado encontrar os piores alunos da
universidade, então o pesquisador trabalharia com a cauda esquerda). Já podemos
raciocinar que com uma cauda de 1% o valor de Zi deve ser entre 2 e 3. Dois desvios
padrão correspondiam a 4,55% de área nas duas caudas (2,23% em uma cauda) e três
desvios padrão correspondia a 0,27% nas duas caudas (0,135% em uma). O valor de Zi
da tabela 3.1 é 2,33. Lembra-se que o valor de Zi vem da seguinte expressão onde
relaciona a distância da média em desvio padrão:
P(Z) = 1% →
Zi = 2,33 =
(X i - média)
desvio padrão
Já sabemos que o valor estimado da amostra para a média das avaliações é 7,0 e que o
valor estimado do desvio padrão é 1,0. Colocando tudo junto, temos então:
2,33 =
(X i - 7,0)
1,0
É fácil mostrar que
11
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
Xi = (2,33)*(1,0) + 7,0 = 9,33.
O conceito final que define os alunos que vão receber prêmios é 9,33.
No mesmo dia da amostragem de 200 alunos, o reitor, muito orgulhoso de sua equipe de
estatísticos, pode anunciar quem entre os 18.000 alunos vão ganhar prêmio: todos os
alunos com conceitos finais acima de 9,33.
0,45
0,4
0,35
Área na
cauda a
direita de
9,33 é 1,0%,
os alunos
premiáveis.
0,3
0,25
0,2
0,15
0,1
0,05
0
4
5
6
7
8
9
9,33
2
2,33
10
Xi conceitos finais
-1
0
1
Zi desvios padrão da
média
.
9,33 = média + 2,33*desvio padrão
9,33 = 7,0 + 2,33*1,0
Figura 3.4 – Alunos premiáveis, relação entre Xi o valor original em unidades
mensuráveis (as notas dos alunos), e Zi o valor padronizado pelo desvio padrão.
3.2.5 Outros exemplos
As possibilidades são inúmeras para este tipo de solução em várias áreas e exemplos.
Para checar a qualidade de um produto fabricado em grandes lotes, cerveja, por
exemplo, podemos calcular quantas latas em um lote de 100.000 ficarão fora dos limites
de especificação de alguma característica relevante como acidez ou volume. Nesse caso
a amostragem é absolutamente necessária porque a inspeção é destrutiva, a lata teria que
ser aberta, e o líquido experimentado!
Na equação para Z, existem 4 parâmetros; e se for conhecido 3 destes parâmetros então
o quarto parâmetro é calculável. No exemplo da universidade, conhecemos a média, o
desvio padrão e o valor de Zi que resulta do tamanho da cauda P(Zi), e,
conseqüentemente, calculamos o valor crítica Xi a média que define os alunos
premiáveis.
Em outras situações, é necessário calcular o valor de Zi e P(Zi) conhecendo Xi, a média,
e o desvio padrão. Num caso comum na fábrica, Xi é um limite de especificação e o
12
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
engenheiro quer saber quanto da sua produção será rejeitada dado à variabilidade do
processo (desvio padrão). A área da cauda é a sua resposta.
Imagina que Xi é limite de especificação para o diâmetro máximo tolerável de um pistão
em 70,010 mm com alvo de 70 mm. O desvio padrão do diâmetro é historicamente
0,0033 mm (3,3 micrometros). Com essas poucas informações podemos responder a
seguinte pergunta, quantos pistões sairão da linha de produção com diâmetros não
conformes acima do limite? Zi é igual a
Zi =
(X i - média)
= (70,010 – 70,000)/0,0033 = 0,010/0,0033 = 3.
desvio padrão
Isso significa que a cauda a direita de Zi é P(Zi) = 0,135% ou 1350 PPM. O gerente da
linha fica satisfeito com esse resultado? Vejam outros exercícios no final deste capítulo.
3.3 Distribuição t (Gosset)
A utilização da distribuição t de Gosset (student t em Inglês), derivada da distribuição
normal, é apropriada quando a amostra possui poucas observações. O fato de ter poucas
observações na amostra contribui para a incerteza das estatísticas estimadas e
especialmente no valor do desvio padrão estimado. Se o desvio padrão já é conhecido
por arquivos históricos da fábrica ou por outras razões, então sempre pode confiar no
uso da distribuição normal, caso contrario terá que usar a distribuição t. Como já foi
visto, as estimativas de amostras pequenas não são absolutamente confiáveis, e é o
papel da distribuição t de levar em conta essa maior incerteza, assim possuindo uma
forma mais achatada no meio e mais inchada nas caudas quando comparada com a
distribuição normal. A definição de “poucas observações” depende da área de estudo e o
propósito da pesquisa. Nas ciências exatas, justamente porque as medições são mais
exatas, como medições feitas em condições laboratoriais, uma amostra pequena pode
possui 100 observações ou até mais exigindo a distribuição t. A natureza mais exata e
controlada das mensurações nas ciências exatas permite uma análise de risco mais
apurada e conseqüentemente a utilização de distribuições de probabilidade como
distribuição t que são mais apropriadas. Por outro lado, nas ciências humanas, as
medições pela própria natureza não são tão exatas e comumente não são feitas em
laboratórios, e então amostras pequenas que obrigam a utilização da distribuição t são
até em torno de 30 elementos. Não há necessidade de buscar mais precisão em
formulações matemáticas mais perfeitas quando os dados não exigem isso e a
distribuição normal seria adequada. Uma boa parte das engenharias fica localizada no
meio entre as ciências sociais e as exatas, deixando a escolha de qual distribuição é mais
apropriado depender da experiência e astúcia do pesquisador. Na figura 3.5, são
apresentadas a distribuição t com pequeno tamanho da amostra e a distribuição normal.
13
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
Na figura, consta-se apenas o lado direito das distribuições.
distribuição normal
distribuição t
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
Distância em desvios padrão
Figura 3.5 – Distribuição normal e distribuição t, comparação de caudas.
Com amostras pequenas, a distribuição t fica bastante achatada, mas a observação mais
importante é que as caudas são relativamente grandes. Com tamanhos de amostra
intermediários, o achatamento é aliviado. Finalmente com amostras grandes, maiores de
100, a distribuição t e a distribuição normal são aparentemente iguais. Pode ver isso nas
últimas linhas da tabela 3.3 e comparando os valores da distribuição t com os valores da
distribuição normal da última linha. Com amostras grandes, não há diferença entre as
distribuições. Hoje em dia a distribuição t é pouco utilizada no chão da fábrica, mas é
cada vez mais solicitada em empresas mais modernas com cultura acadêmica mais
desenvolvida, querendo desempenho organizacional maior. A distribuição t aparece
várias vezes nos capítulos seguintes.
GRAU DE
LIBERDADE
1
2
3
4
ÁREA DE UMA ÚNICA CAUDA –
UNICAUDAL %
5
2,5
1,25
0,5
0,25
0,135
ÁREA SOMADA NAS DUAS CAUDAS –
BICAUDAL %
10
5
2,5
1,0
0,5
0,27
ÁREA SOMADA DA ESQUERDA A DIREITA –
ACUMULADA %
95
97,5
98,75
99,5
99,75
99,865
6,31
2,92
2,35
2,13
12,71
4,30
3,18
2,78
25,45
6,21
4,18
3,50
63,66
9,92
5,84
4,60
127,32
14,09
7,45
5,60
235,78
19,21
9,22
6,62
14
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
35
36
38
39
41
43
46
48
51
54
58
63
68
74
82
91
103
2,02
1,94
1,89
1,86
1,83
1,81
1,80
1,78
1,77
1,76
1,75
1,75
1,74
1,73
1,73
1,72
1,72
1,72
1,71
1,71
1,71
1,71
1,70
1,70
1,70
1,70
1,70
1,69
1,69
1,69
1,69
1,69
1,68
1,68
1,68
1,68
1,68
1,68
1,67
1,67
1,67
1,67
1,67
1,66
1,66
1,66
2,57
2,45
2,36
2,31
2,26
2,23
2,20
2,18
2,16
2,14
2,13
2,12
2,11
2,10
2,09
2,09
2,08
2,07
2,07
2,06
2,06
2,06
2,05
2,05
2,05
2,04
2,04
2,04
2,03
2,03
2,03
2,02
2,02
2,02
2,02
2,01
2,01
2,01
2,00
2,00
2,00
2,00
1,99
1,99
1,99
1,98
3,16
2,97
2,84
2,75
2,69
2,63
2,59
2,56
2,53
2,51
2,49
2,47
2,46
2,45
2,43
2,42
2,41
2,41
2,40
2,39
2,38
2,38
2,37
2,37
2,36
2,36
2,36
2,35
2,35
2,34
2,34
2,33
2,33
2,33
2,32
2,32
2,31
2,31
2,31
2,30
2,30
2,29
2,29
2,28
2,28
2,27
Robert Wayne Samohyl, Ph.D.
4,03
3,71
3,50
3,36
3,25
3,17
3,11
3,05
3,01
2,98
2,95
2,92
2,90
2,88
2,86
2,85
2,83
2,82
2,81
2,80
2,79
2,78
2,77
2,76
2,76
2,75
2,74
2,74
2,73
2,72
2,72
2,71
2,71
2,70
2,70
2,69
2,68
2,68
2,67
2,66
2,66
2,65
2,64
2,64
2,63
2,62
4,77
4,32
4,03
3,83
3,69
3,58
3,50
3,43
3,37
3,33
3,29
3,25
3,22
3,20
3,17
3,15
3,14
3,12
3,10
3,09
3,08
3,07
3,06
3,05
3,04
3,03
3,02
3,01
3,01
3,00
2,99
2,98
2,98
2,97
2,96
2,95
2,94
2,93
2,93
2,92
2,91
2,90
2,89
2,88
2,88
2,87
5,51
4,90
4,53
4,28
4,09
3,96
3,85
3,76
3,69
3,64
3,59
3,54
3,51
3,48
3,45
3,42
3,40
3,38
3,36
3,34
3,33
3,32
3,30
3,29
3,28
3,27
3,26
3,25
3,24
3,23
3,22
3,21
3,20
3,19
3,18
3,17
3,16
3,15
3,14
3,13
3,12
3,11
3,10
3,09
3,08
3,07
15
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
118
139
200
DISTRIBUIÇÃO
NORMAL (∞)
1,66
1,66
1,65
1,64
1,98
1,98
1,97
1,96
2,27
2,27
2,26
2,24
Robert Wayne Samohyl, Ph.D.
2,62
2,61
2,60
2,58
2,86
2,85
2,84
2,81
3,06
3,05
3,04
3,00
Tabela 3.3 – Distribuição de t de Gosset
3.4 Algumas considerações sobre as distribuições F e χ2 (Chi quadrado)11
As distribuições F e χ2 (Chi quadrado) também têm a sua origem na distribuição normal,
e se aplicam em situações especificas relatadas principalmente no capítulo 6 (Teste de
hipótese) e na terceira parte do livro sobre relações entre variáveis no contexto de
regressão e a estimação de parâmetros de equações. É importante enfatizar que essas
duas distribuições são derivadas da distribuição normal exigindo os mesmos cuidados.
Com raras exceções, as variáveis em análise devem ser distribuídas normalmente para
garantir conclusões estatísticas de qualidade.
A distribuição de χ2 (chi quadrado) é a soma de variáveis quadradas que seguem a
distribuição normal padronizada (Z). Podemos escrever assim
k
 2   Zi2
i 1
Os graus de liberdade são o número (k) de variáveis Zi na fórmula. É considerada uma
distribuição para grandes amostras e conseqüentemente o desvio padrão das populações
é conhecido.
A distribuição F é o resultado da divisão de duas variáveis χ2.
 22
F(gl2 ,gl1 ) 
gl2

2
1
gl1
Nas complexidades da matemática estatística, quando gl2 é igual a um, a distribuição F e
t de Gosset são equivalentes.
Este capítulo é apenas uma rápida introdução a estatística de variáveis mensuráveis. O
aluno interessado em aprimorar os conhecimentos deve consultar as referencias que
constam no Prefácio.
3.5 Exercícios:
11
Esta seção é apenas introdutória e certamente vai deixar muitas dúvidas para o iniciante na área de
estatística. Contudo, as dúvidas devem ficar esclarecidas no decorrer dos capítulos seguintes.
16
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
1. Para a distribuição normal, qual é a probabilidade de uma mensuração ficar no
máximo a distância de 1,5 desvios padrão da média? Sua resposta pode ser aproximada.
Resposta: 0,866
2. Para mensurações que seguem a distribuição normal, num total de 10.000
mensurações, quantas vão ficar no máximo a distância de 2,5 desvios padrão da média?
Sua resposta pode ser aproximada.
Resposta: 9876
3. Para a distribuição normal, qual é a probabilidade da mensuração de uma peça ficar
no máximo a distância de 3,5 desvios padrão da média das mensurações? Sua resposta
aproximada é
Resposta: 0,99953
4. Para mensurações que seguem a distribuição normal, qual é a probabilidade de uma
mensuração ficar fora dos limites de especificação de três desvios padrão da média? Sua
resposta aproximada em PPM é
Resposta: 2700.
5. Para a distribuição normal, qual é a probabilidade de rejeitar uma peça cujo único
limite de especificação é o superior e fica a distância de seis desvios padrão da média?
Sua resposta aproximada é
Resposta: 0,001 PPM
6. Um engenheiro rejeita todo produto que está fora dos limites de especificação. Nesse
momento, a linha está produzindo uma taxa de 10% de rejeito simetricamente acima e
abaixo dos limites de especificação. No entanto, ele é descontente com a alta taxa de
rejeição e quer uma taxa ao máximo de 2%. Ele vê duas alternativas: ou diminuir o
desvio padrão do processo ou aumentar os limites de especificação. Qual é a alternativa
mais econômica no curto prazo? Outra questão importante é se o engenheiro optar para
diminuir o desvio padrão do processo, qual é a relação entre o desvio padrão novo que é
menor e o desvio padrão velho que é obviamente maior? Elaborar sua resposta usando a
distribuição normal padronizada.
Resposta: Em primeiro lugar, a alteração dos limites de especificação é sempre mais
fácil que a alteração do desvio padrão do processo, embora a base conceitual do limite
de especificação tenha mais a ver com a engenharia da peça e não considerações
comerciais.
Utilizando a distribuição normal padronizada, queremos comparar a diferença entre o
desvio padrão do processo antes das melhorias e depois das melhorias, em outras
palavras, quanto foi diminuído o tamanho do desvio padrão. Vamos comparar as caudas
da distribuição normal padronizada antes e depois das melhorias. Antes, a cauda é igual
a 5% e depois é igual a 1%. A distância entre o limite de especificação e a média em
unidades originais fica constante. Antes das melhorias, a distância é 1,64 desvios padrão
velhos e depois das melhorias é 2,33 desvios padrão novos. Em outra forma, 1,64
desvios padrão velhos = 2,33 desvios padrão novos. A relação entre desvios padrão
17
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis
Controle Estatístico de Qualidade (CEQ):
Robert Wayne Samohyl, Ph.D.
novos e velhos é 1,64/2,33 = 0,7. Portanto, o desvio padrão vai ter que diminuir em
aproximadamente 30% para diminuir a taxa de rejeição de 10% para 2%.
3.6 Referências
Box, George E. P.; Cox, D. R. (1964). "An analysis of transformations". Journal of the
Royal Statistical Society, Series B 26: 211–246. http://www.jstor.org/stable/2984418.
18
Capítulo 3 As distribuições de probabilidade mais importantes em controle estatístico de qualidade
(CEQ): variáveis mensuráveis