1 - Matematicogrs

2ª LISTA DE EXERCÍCIOS PARA O ENSINO MÉDIO DE MATEMÁTICA 2015
ELABORADA PELA EQUIPE GRE RCF SUL
FORMAÇÃO CONTINUADA DE PROFESSORES
Eixo – Grandezas e Medidas
Matriz Curricular: Conteúdo Princípio de Cavaliere
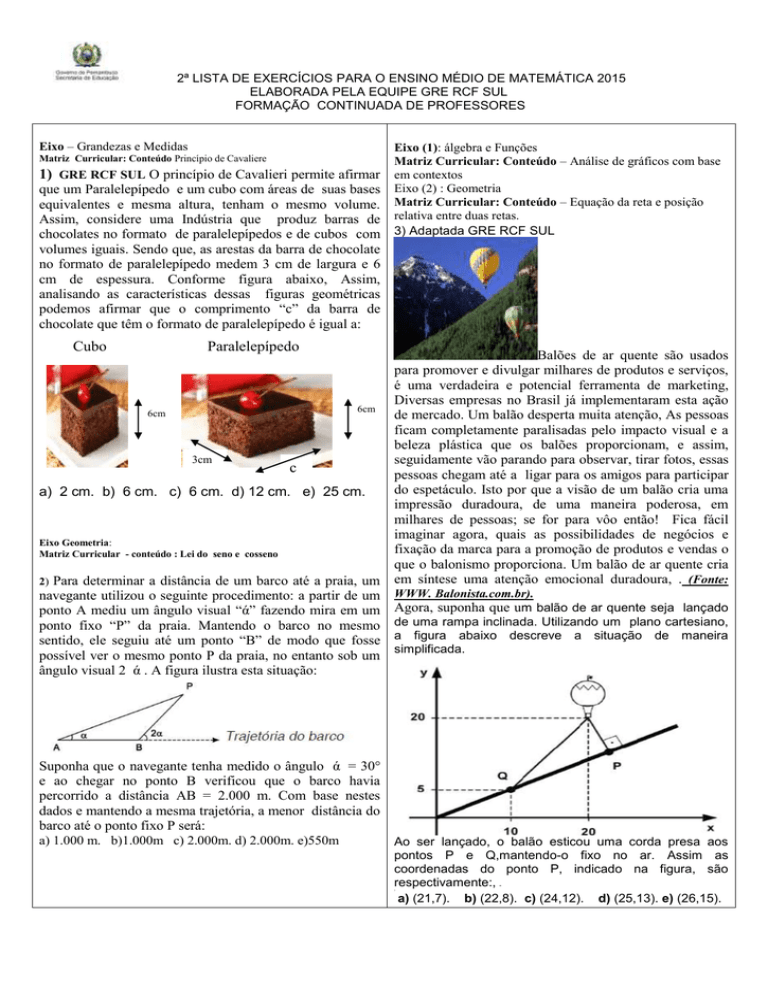
1) GRE RCF SUL O princípio de Cavalieri permite afirmar
que um Paralelepípedo e um cubo com áreas de suas bases
equivalentes e mesma altura, tenham o mesmo volume.
Assim, considere uma Indústria que produz barras de
chocolates no formato de paralelepípedos e de cubos com
volumes iguais. Sendo que, as arestas da barra de chocolate
no formato de paralelepípedo medem 3 cm de largura e 6
cm de espessura. Conforme figura abaixo, Assim,
analisando as características dessas figuras geométricas
podemos afirmar que o comprimento “c” da barra de
chocolate que têm o formato de paralelepípedo é igual a:
Cubo
Eixo (1): álgebra e Funções
Matriz Curricular: Conteúdo – Análise de gráficos com base
em contextos
Eixo (2) : Geometria
Matriz Curricular: Conteúdo – Equação da reta e posição
relativa entre duas retas.
3) Adaptada GRE RCF SUL
Paralelepípedo
Balões de ar quente são usados
para promover e divulgar milhares de produtos e serviços,
é uma verdadeira e potencial ferramenta de marketing,
Diversas empresas no Brasil já implementaram esta ação
6cm
6cm
de mercado. Um balão desperta muita atenção, As pessoas
ficam completamente paralisadas pelo impacto visual e a
beleza plástica que os balões proporcionam, e assim,
3cm
seguidamente vão parando para observar, tirar fotos, essas
c
pessoas chegam até a ligar para os amigos para participar
do espetáculo. Isto por que a visão de um balão cria uma
a) 2 cm. b) 6 cm. c) 6 cm. d) 12 cm. e) 25 cm.
impressão duradoura, de uma maneira poderosa, em
milhares de pessoas; se for para vôo então! Fica fácil
imaginar agora, quais as possibilidades de negócios e
Eixo Geometria:
fixação da marca para a promoção de produtos e vendas o
Matriz Curricular - conteúdo : Lei do seno e cosseno
que o balonismo proporciona. Um balão de ar quente cria
2) Para determinar a distância de um barco até a praia, um em síntese uma atenção emocional duradoura, . (Fonte:
navegante utilizou o seguinte procedimento: a partir de um WWW. Balonista.com.br).
ponto A mediu um ângulo visual “ά” fazendo mira em um Agora, suponha que um balão de ar quente seja lançado
ponto fixo “P” da praia. Mantendo o barco no mesmo de uma rampa inclinada. Utilizando um plano cartesiano,
sentido, ele seguiu até um ponto “B” de modo que fosse a figura abaixo descreve a situação de maneira
possível ver o mesmo ponto P da praia, no entanto sob um simplificada.
ângulo visual 2 ά . A figura ilustra esta situação:
Suponha que o navegante tenha medido o ângulo ά = 30°
e ao chegar no ponto B verificou que o barco havia
percorrido a distância AB = 2.000 m. Com base nestes
dados e mantendo a mesma trajetória, a menor distância do
barco até o ponto fixo P será:
a) 1.000 m. b)1.000m c) 2.000m. d) 2.000m. e)550m
Ao ser lançado, o balão esticou uma corda presa aos
pontos P e Q,mantendo-o fixo no ar. Assim as
coordenadas do ponto P, indicado na figura, são
respectivamente:,
a) (21,7). b) (22,8). c) (24,12). d) (25,13). e) (26,15).
m
)
2ª LISTA DE EXERCÍCIOS PARA O ENSINO MÉDIO DE MATEMÁTICA 2015
ELABORADA PELA EQUIPE GRE RCF SUL
FORMAÇÃO CONTINUADA DE PROFESSORES
Eixo: Álgebra e Funções
Matriz Curricular - Conteúdo: Teorema fundamental da álgebra.,
Relações de Girard, teorema de Briot Rufini
4. (Ufsj 2012) Considere a função polinomial definida por
P(x) = x4 – 3x 3 – 3x² + 11x –6, neste caso, é CORRETO
afirmar que em relação a P(x):
a) P(10) é um número de cinco algarismos.
b) P(x) tem quatro raízes distintas.
c) na divisão por x + 2, P(x) apresenta resto igual a 4.
d) Px) é divisível por x – 1.
Eixo: álgebra e Funções
Matriz Curricular: Conteúdo: Conjunto dos números
complexos,Forma algébrica dos números complexos, Representação
geométrica dos números complexos, conjugado de um número
complexo, operações com números complexos :forma algébrica,
Módulo de um número complexo, forma trigonométrica de um número
complexo,
(Ufrj) Em um jogo de sinuca,uma mesa está
localizada com centro na origem do plano complexo,
conforme mostra a figura a seguir. Após uma tacada
do centro O, a bola preta segue na direção de Z=1+i,
.
bate em A, indo em seguida até B e parando,
Eixo: álgebra e Funções
Matriz Curricular: Conteúdo : Operações com polinômios .Equações Conforme demonstra a figura a seguir, Neste caso,
polinomiais. Função Polinomial, Valor numérico de um polinômio,
Encontre o ponto Z = a+bi, onde a bola preta teria
igualdade de polinômio, Decomposição de fatores de primeiro grau.
5. (UERJ) Um ciclista e um corredor começam, juntos, parado se a tacada tivesse sido dada, com a mesma
uma competição. A curva abaixo, cuja equação é dada por intensidade, na direção e sentido do conjugado de Z.
7.
e = t3 + at2 + bt + c, representa a posição e, em metros, do
ciclista, em função do tempo t, em segundos, em que a, b
e c são números reais fixos. No instante em que o ciclista
parte da posição zero, o corredor inicia um movimento,
descrito pela equação e = 4t, na mesma pista e no mesmo
sentido. Podemos afirmar que a posição mais afastada da
origem na qual o ciclista e o corredor voltam a se encontrar
é igual a :.
Eixo: Álgebra e Funções
Matriz Curricular - Conteúdo:Operações com números
complexos na forma trigonométrica,
8. Considere as seguintes Proposições:
I) Dada a figura abaixo Podemos afirmar que o número
complexo z = x + yi será representado no plano argand
Gaus, na forma z= r (sen θ + i cós θ ). Onde r = √(x² + y²)
a) 20metros
b) 25metros c) 30 metros d) 35metros
Eixo: Álgebra e Funções
Matriz Curricular - Conteúdo:Relações de Girard e Equações
polinomiais
6.. Sabe-se que
dado um polinômio de coeficiente real,
se z= a +bi é raiz desse polinômio com b≠0, então, o
conjugado z = a – bi também é raiz do polinômio,
concomitantemente, um polinômio de coeficientes
racionais; se (a + √b) é raiz desse polinômio com b≭0
então a raíz (a - √b) , também é raiz desse polinômio,
neste caso, considere o polinômio: P(x) = x5 – 9x4 +22x3 14x² +21x -5 ; tendo duas de suas raízes que são : i e 2+√3
podemos afirmar que as demais raízes são :
a) (–i , 2 -√3 e -5)
b) (2i , 2 -√3 e -5)
c) (–i , 2 -√3 e -3)
d) (–i , 2 -√3 e 5)
II) Dados os números complexos z1 = 6∙(cos30o + i∙sen
30o) e z2 = 3∙(cos15o + i∙sen 15o), o valor de z1 ∙ z2 é igual
a : 18∙(cos45o - i∙sen 45o )
III) Dados z = 22∙(cos120o + i∙sen 120o) e c = 11∙(cos90o
+i∙sen 90o), o valor de z/c é igual a 2(cos30o +i∙sen 30o),
a) Apenas a 1ª Proposição está Correta
b) As proposições I e III estão corretas
c) Apenas a proposição III está correta
d) Apenas a Proposição II está correta
2ª LISTA DE EXERCÍCIOS PARA O ENSINO MÉDIO DE MATEMÁTICA 2015
ELABORADA PELA EQUIPE GRE RCF SUL
FORMAÇÃO CONTINUADA DE PROFESSORES
Descritores
D9) Relacionar a determinação do ponto de intersecção de duas
ou mais retas com a resolução de um sistema de equação
9. Na figura, abaixo, estão representados um sistema de
equações e os gráficos de duas retas.
4x – 3y = P
X + 3y = Q
Descritores
D12 Resolver problemas envolvendo áreas de figuras planas
12. (Concurso público – Eletrobrás). A figura abaixo
representa a planta de um apartamento.
A área total é de (m2):
(A) 56; (B) 58; (C) 62; (D) 64; (E) 80.
D13 Resolver problemas que envolvam a área total ou volume
de um sólido (prisma, pirâmide,cilindro, cone e esfera)
Os valores de P e Q para que o gráfico corresponda à
solução do sistema são
A) 12 e 2.
B) – 9 e 6.
C) – 36 e 6. D) – 6 e 4.
13 , A figura, abaixo, representa um “silo”, muito
utilizado nas fazendas para armazenar grãos. Ele é
composto de um cone e um cilindro e suas dimensões
estão indicadas na figura abaixo.
D10) Reconhecer, dentre as equações do 2º grau com duas
incógnitas, as que representam circunferência
10. Dentre as equações abaixo, pode-se afirmar que a de
uma circunferência é:
a) ( x – 1)² + y² = 25
c) x² + y² = - 16
e) x² - y² - 4x =9
b) x² - y -4x = - 3
d) x² - y -9 = 0
A capacidade máxima de armazenagem de grãos nesse
silo é de
A) 20π m3.B) 24π m3. C) 32π m3. D) 96π m3.
D11) Resolver problema envolvendo perímetro de figuras planas
11. A figura, abaixo, representa a planta de uma praça
triangular. Ela é contornada por uma calçada e há um
atalho, representado na figura pelo caminho RQ,
perpendicular a um dos lados.
D14 Identificar a localização de números reais na reta numérica
14 . (SADEAM). Observe a reta numérica abaixo
Considerando que – 4 < x < 4, um dos pontos que x
poderá assumir é
(A) I
(B) P
(C) M
(D) H (E) Q
D15 Resolver problemas que envolva variações propOrcionais
direta ou inversa
Para ir do ponto M ao ponto P, Júlia percorreu o trecho
MQRP, andando sempre sobre a calçada. o perímetro
percorrido por Júlia foi igual a :
A) 35 m. B) 48 m. C) 52 m. D) 72 m.
15. Em Aposentolândia foi implantada a chamada
“fórmula 96”. Por essa fórmula, um trabalhador tem
direito à aposentadoria, quando a soma de sua idade com o
número de anos trabalhados é igual a 96. Nesse país, qual
a idade mínima de aposentadoria para uma pessoa que
comece a trabalhar com 24 anos de idade?
A) 60. B) 72.
C) 84. D) 96.
2ª LISTA DE EXERCÍCIOS PARA O ENSINO MÉDIO DE MATEMÁTICA 2015
ELABORADA PELA EQUIPE GRE RCF SUL
FORMAÇÃO CONTINUADA DE PROFESSORES