Aula 2 – Estática dos fluidos - Universidade Federal de Pelotas

UNIVERSIDADE FEDERAL DE PELOTAS - UFPEL
CENTRO DE ENGENHARIAS - CENG
DISCIPLINA: MECÂNICA DOS FLUIDOS
A ESTÁTICA DOS FLUIDOS
Prof. Dr. Hugo Alexandre Soares Guedes
E-mail: [email protected]
wp.ufpel.edu.br/hugoguedes
1º Semestre de 2017
DEFINIÇÃO
É a parte da Mecânica dos Fluidos que
estuda fluidos em equilíbrio sujeitos a ação
da gravidade e também sua interação com
os corpos sólidos.
CONCEITO DE PRESSÃO
A pressão aplicada sobre uma superfície
pode ser definida pela relação entre a força
aplicada e a área dessa superfície, e pode
ser numericamente calculada pela aplicação
da equação:
TRANSMISSÃO DE PRESSÃO
1. Referência:
•
Vácuo ou zero absoluto: pressão absoluta
•
Pressão atmosférica: pressão efetiva ou pressão
manométrica
PRESSÃO ATMOSFÉRICA:
EXPERIÊNCIA DE TORRICELLI
• Barômetro de mercúrio
O barômetro é um dispositivo
para medir a pressão atmosférica.
A pressão atmosférica (ponto A)
equilibra uma coluna de mercúrio
de aproximadamente 76 cm de
altura.
ATMOSFERA TÉCNICA:
EXPERIÊNCIA DE PASCAL
PRESSÃO EM TORNO DE UM PONTO DE
UM FLUIDO EM REPOSUSO
A pressão num ponto de um fluido em
repouso é a mesma em qualquer direção.
LEI DE PASCAL
“A pressão
aplicada num ponto de um fluido
em repouso transmite-se integralmente a
todos os pontos do fluido.”
LEI DE PASCAL
PRENSA HIDRÁULICA OU
ELEVADOR HIDRÁULICO
A prensa hidráulica ou o elevador hidráulico utiliza a Lei de
Pascal para ampliar forças.
De acordo com a Lei de Pascal:
A1 < A2
F1 < F 2
ELEVADOR HIDRÁULICO (EXEMPLO)
Aplicando uma força F1 de 50 N no pistão de uma prensa
cilíndrica de R1 = 0,5 cm e R2 = 4,0 cm. Qual será a força no
pistão 2?
Solução:
F1 / A1 = F2 / A2 (pela Lei de Pascal)
Logo: F2 = F1 x (A2 / A1)
F2 = 50 x (ᴨ x 4² / ᴨ x 0,5²)
F2 = 3200 N
TEOREMA DE STEVIN
“A diferença de pressão entre dois pontos
de um fluido em repouso é igual ao produto
do peso específico do fluido pela diferença
de cota dos dois pontos”
TEOREMA DE STEVIN - CONCLUSÕES
1. Na diferença de pressão entre dois pontos não interessa a
distância entre eles, mas a diferença de cotas.
2. A pressão dos pontos num mesmo plano ou nível horizontal é a
mesma, desde que os pontos estejam localizados no mesmo
fluido.
3. O formato do recipiente não é importante para o cálculo da
pressão em algum ponto.
4. Se a pressão na superfície livre de um líquido contido num
recipiente for nula, a pressão num ponto à profundidade (h)
dentro do líquido será dada por: P = γh.
5. Nos gases, como o peso específico é pequeno, se a diferença de
cota entre dois pontos não for muito grande, pode-se
desprezar a diferença de pressão entre eles.
TEOREMA DE STEVIN - APLICAÇÕES
1. Princípio dos Vasos Comunicantes
As superfícies livres de um líquido em equilíbrio contido em
recipientes interligados (vasos comunicantes) permanecem
sempre horizontais e num mesmo plano, independente da
forma dos vasos.
TEOREMA DE STEVIN - APLICAÇÕES
2. Pressão e força no fundo de um recipiente
TEOREMA DE STEVIN - APLICAÇÕES
3. Equilíbrio de dois líquidos de pesos específicos
diferentes
As camadas se superpõem na ordem crescente
de seus pesos específicos, sendo plana e horizontal
a superfície de contato.
TEOREMA DE STEVIN - APLICAÇÕES
4.
Vasos comunicantes com Líquidos diferentes
CARGA DE PRESSÃO
A pressão em um ponto qualquer de um líquido pode ser
imaginada como sendo causada pelo peso da coluna vertical
do líquido. A altura “h” dessa coluna é chamada de carga e
é expressa em termos de “metro de líquido”.
APLICAÇÕES
1. Converter a pressão de 1,5 kgf/cm² em:
a) metro de coluna de água (mca).
b) metro de coluna de mercúrio (mcHg).
Sabendo: γágua = 1000 kgf/m³ e γHg = 13600 kgf/m³
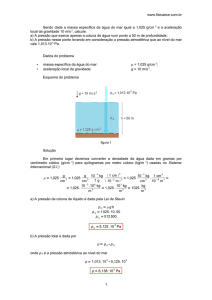
2. Um mergulhador está trabalhando na profundidade de 20 metros
da superfície do mar (γ = 1025 kgf/m³ ). Um barômetro instalado
no nível do mar acusa pressão de 760 mmHg. Qual a pressão
absoluta sobre o mergulhador?
APLICAÇÕES
3. Seja um tubo com êmbolo bem ajustado. Façamos baixar sua face
interna num recipiente com líquido e elevemos gradualmente este
êmbolo. O líquido subirá no cilindro atrás do êmbolo e se elevará
até uma certa altura h em relação à superfície livre onde atua a
pressão atmosférica.
a) Qual a altura máxima se o líquido for a água?
b) E se for gasolina?
Dados: γágua = 1000 kgf/m³ ; γgasolina = 750 kgf/m³
Patm = 1,033 kgf/cm²