GENÉTICA DE POPULAÇÕES:
Noções básicas com
aplicação em aquacultura
RITA CASTILHO
GRUPO BIODIVERSIDADE E CONSERVAÇÃO
CENTRO DE CIÊNCIAS DO MAR
UNIVERSIDADE DO ALGARVE
CAMPUS DE GABELAS
FARO PORTUGAL
([email protected])
Índice
Introdução .................................................................................................................................... 1
Resumo histórico ........................................................................................................................ 3
Diversidade Genética .................................................................................................................. 4
Estrutura genética das populações ........................................................................................... 8
Equilíbrio de Hardy-weinberg................................................................................................... 10
Equilíbrio de Hardy-weinberg................................................................................................... 11
Deriva Genética ......................................................................................................................... 17
Dimensão efectiva da população ............................................................................................. 21
Consanguinidade ...................................................................................................................... 23
Mutação ...................................................................................................................................... 27
Migração ..................................................................................................................................... 29
Selecção ..................................................................................................................................... 32
Nota: As fotografias da página 3, e as figuras 1, 3, 5, 6 e 9 necessitam de
autorização para serem reproduzidas.
INTRODUÇÃO
A Genética de Populações procura compreender e fazer previsões dos
efeitos de fenómenos genéticos como a segregação, recombinação,
transposição e mutação sobre as populações, tendo em conta factores
ecológicos e evolucionários como a dimensão da população, padrões de
reprodução, distribuição geográfica de indivíduos, migração e selecção.
As questões frequentemente abordadas em genética de populações
incluem: i) a amplitude da variação genética encontrada nas populações
naturais, ii) os processos evolutivos que moldam a estrutura genética das
populações, iii) os processos responsáveis pelo surgimento de divergência
genética entre populações, iv) a influência das características biológicas das
populações, tais como o tipo de reprodução, a fecundidade e a estrutura
etária, sobre o pool genético das populações?
A genética de populações é hoje uma disciplina fundamental com larga
aplicação quer na classificação sistemática, quer nas acções de conservação
da natureza, quer na biologia pesqueira e aquacultura.
Nos programas de avaliação da diversidade biológica, e de conservação
de recursos, nomeadamente na gestão de parques, reservas naturais e jardins
zoológicos é imperiosa a avaliação das consanguinidade no intuito da
manutenção da diversidade genética.
Nos programas de selecção praticados nas pisciculturas que incluem
reprodução de organismos, é essencial assegurar-se em simultâneo a
manutenção da diversidade genética e o apuramento de características,
elementos frequentemente opostos.
O estudo da variabilidade genética das populações pode-se realizar de
formas distintas atendendo aos distintos caracteres a analisar e de acordo com
diferentes metodologias que poderemos englobar em dois grandes grupos:
Genética Quantitativa e Genética Qualitativa.
A Genética Quantitativa (Falconer, 1989) dedica-se ao estudo de caracteres
que formam uma série gradativa de um extremos a outro sem que possam ser
classificados em tipos bem demarcados. Estes caracteres não seguem, na
realidade, os padrões Mendelianos de heritabilidade para um só locus. Noutras
palavras, não existe correspondência directa entre fenótipo e genótipo, como
noutras ocasiões. Este tipo de caracteres possui interesse quer teórico
(evolutivo), quer aplicado (comercial). Uma fatia importante das alterações
evolutivas produz-se por selecção natural sobre pequenas variações dos
1
organismos como a forma, a dimensão, a fisiologia ou o comportamento, por
exemplo. A análise da variação contínua requer uma metodologia especial,
biométrica, para descrever sistemas poligénicos dos caracteres quantitativos
em termos de efeitos fenotípicos e de forma globalizada.
A Genética Qualitativa, por seu lado, analisa caracteres descontínuos, como
por exemplo, côr dos olhos, grupos sanguíneos ou sistemas enzimáticos. Os
polimorfismos enzimáticos possuem grandes vantagens nos estudos de
genética de populações. São caracteres determinados geralmente por um só
locus e cujo fenótipo (neste caso as suas propriedades catalíticas) possui um
evidente significado fisiológico podendo ser quantificado de forma objectiva.
Com efeito, é com facilidade que a partir de dados deste tipo, se estabelecem
genótipos para determinados loci e a partir de estes se estimam parâmetros
genéticos de populações (frequências genotípicas, alélica, heterozigotia,
polimorfismo).
Tendo em atenção os diferentes níveis de preparação dos leitores deste
capítulo, pretendemos somente introduzir noções muito básicas de genética de
populações, noções essas que tenham aplicação em aquacultura e que
forneçam uma visão correcta, mas necessariamente limitada, aos iniciados
nesta área. Existem textos relativamente actuais que aconselhamos vivamente
ao estudante que queiram aprofundar aspectos vários da genética de
populações aplicada à aquacultura, como por exemplo: Beaumont (2003);
Dunham (2003); Hallerman (2003) and Lutz (2001).
2
RESUMO HISTÓRICO
A Genética de Populações, enquanto área de trabalho, iniciou-se com os
trabalhos de Fisher (1918), Wright (1921) e Haldane (1932). De facto, esses
autores consideraram muitos dos problemas fundamentais da Genética de
Populações e só mais recentemente, com a descoberta de grande quantidade
de variabilidade genética, revelada pela electroforese, surgiram novas áreas de
experimentação e teorização.
Sir Ronald A. Fisher (1890-1962) de naturalidade britânica,
é mais conhecido pela sua contribuição na área da
estatística. No entanto, durante a sua vida Fisher interessouse pela genética e a sua obra The Genetical Theory of
Natural Selection (1930) constituiu um marco na síntese entre
a selecção darwiniana e a genética. A sua contribuição
traduz-se no desenvolvimento do conceito de selecção
progressiva e consanguinidade e na estimação das frequências alélicas,
intensidade
de
selecção
e
coeficiente
de
consanguinidade.
http://www.harvardsquarelibrary.org/unitarians/wright-sewall.html
Sewall Wright (1889-1988), americano, foi um dos primeiros cientistas a
reconhecer a relação entre genes e enzimas. A sua
contribuição para a análise da consanguinidade, da
repercussão da dimensão finita da população (em que
utilizou uma aproximação matemática particularmente
engenhosa), e muitos outros tópicos foi fundamental para a
genética de populações. De facto, a deriva genética é muitas
vezes referida como o efeito de Sewall Wright.
(http://www.harvardsquarelibrary.org/unitarians/wrightsewall.html)
John Burdon Sanderson Haldane (1892-1964) britânico,
contribuiu essencialmente para a teoria matemática da selecção
num único locus. Usando a selecção e mutação como factores
que conjuntamente afectam as frequências alélicas, Haldane
derivou o equilíbrio que resulta do balanço entre estes dois
factores. (http://www.spartacus.schoolnet.co.uk/SPhaldane.htm)
3
DIVERSIDADE GENÉTICA
Do ponto de vista da Genética de Populações, o atributo mais importante de
uma população é a sua variabilidade genética, já que esta constitui a matéria
prima sobre a qual a mutação, a migração, a deriva genética e especialmente a
selecção natural vão actuar, permitindo a adaptação, especiação e evolução
do mundo vivo.
O tipo de características morfológicas utilizadas na sistemática, por
exemplo, de peixes, número de escamas da linha lateral, raios da barabatana
caudal, arcos branquiais, posição da bexiga natatória etc, não têm equivalente
noutros grupos animais, como por exemplo as aves. Desse modo são
necessárias outras características, nomeadamente dados provenientes da
genética molecular, que permitam comparações entre grupos muito distintos,
de modo a permitirem a comparação directa de níveis de diferenciação
genética.
Só a partir dos anos 50, com o advento com o desenvolvimento das técnicas
moleculares, nomeadamente da electroforese isoenzimática, é que foi possível
a obtenção de dados sobre a variação genética das populações. Não cabe nos
objectivos deste capítulo a referência e desenvolvimento de métodos
moleculares.
A variabilidade genética pode ser medida através de vários parâmetros
como o polimorfismo, a heterozigotia observada, a diversidade alélica ou ainda
a distância genética e que podem ser definidos da seguinte forma:
Polimorfismo, P
Px
em que:
x - loci polimórficos, n - loci analisados
n
Cavalli-Sforza and Bodner (1971) definiram polimorfismo genético
como a ocorrência, num conjunto de indivíduos, de dois ou mais alelos
num locus, cada com apreciável frequência. Relativamente à frequência,
são vulgarmente utilizados dois níveis, sobretudo no que diz respeito às
aloenzimas, considerando-se um locus polimórfico aquele em que o
alelo mais comum tem uma frequência igual ou inferior a 0.99 (P0.99),
de emprego menos frequente, ou o nível mais comum , em que o alelo
mais comum tem uma frequência igual ou inferior a 0.95 (P0.99). A taxa
de polimorfismo corresponde assim ao número de loci polimórficos,
relativamente ao número de loci analisados, sendo pois um índice
sujeito à dimensão da amostra.
4
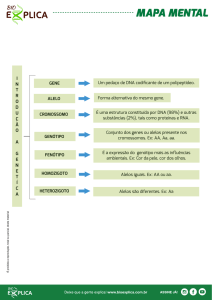
CAIXA 1. TERMINOLOGIA BÁSICA.
Gene: termo geral que se refere à entidade física transmitida pelos
progenitores à descendência; geralmente designa uma entidade codificante de
um característica ou proteína.
Locus/Loci: posição que um gene ocupa num cromosoma ou num segmento
de DNA; exemplo, o segmento de DNA que codifica a enzima isocitrato
desidrogenase é um locus diferente do que codifica a hemoglobina.
Alelo: diferentes formas de um gene, isto é, diferentes sequências de DNA no
mesmo locus (A1, A2).
Genótipo: a combinação dos alelos de um locus num dado indivíduo (A1A1,
A1A2, A2A2), ou dos alelos de vários loci (A1A1B1B2).
Genoma: todo o material genético de uma espécie ou indivíduo.
Heterozigoto: um indivíduo com 2 alelos diferentes num dado locus (A 1A2).
Homozigoto: um indivíduo com duas cópias do mesmo alelo num dado locus
(A1A1, A2A2).
Heterozigoto: um indivíduo com dois alelos distintos num dado locus (A 1A2,
B1B2).
Frequência alélica: a frequência de um dado alelo numa população. Se uma
população tem por exemplo 80 indivíduos A 1A1, e 20 A1A2, então existem 180
cópias do alelo A1 (80x2+20) e 20 do alelo A2. Portanto o alelo A1tem uma
frequência de 0.9 e o A2 tem uma frequência de 0.1.
Locus polimórfico: um locus é polimorfico se a população apresenta mais de
um alelo.
Locus monomórfico: um locus é monomórfico se a população apresenta um
só alelo, e nesse caso todos os indivíduos são homozigóticos para o mesmo
alelo.
Genótipo: conjunto de variantes de DNA encontradas num ou mais loci num
indivíduo.
Fenótipo: a expressão do genótipo.
Proporção de loci polimórficos (P): proporção do número de loci polimórficos
em relação ao número total de loci.
Heterozigotia média (H): Somatório das frequências de todos os loci
heterozigóticos em relação ao total de loci amostrados.
Diversidade alélica (A): número médio de alelos por locus, calculada a partir
do quadrado das frequências alélicas.
Distância genética: uma medida da diferença genética entre populações ou
espécies.
5
Heterozigotia média observada,
H
o
A heterozigotia observada de um dado locus é a proporção de
indivíduos heterozigóticos observados nesse locus. A heterozigotia
média observada é a heterozigotia observada ponderada pelo número
de locus estudado. Um indivíduo que tem 2 alelos diferentes num dado
locus diz-se que é heterozigoto nesse locus. Se a população tem 2 ou
mais alelos nesse locus, e a frequência do alelo mais comum não é
maior que 95%, a população diz-se polimorfica nesse locus.
Heterozigotia média esperada,
H
e
A heterozigotia esperada (teórica) de um dado locus é calculada a partir
das frequências alélicas num dado locus (Nei, 1975):
em que: pi é a frequência do alelo i de um total de k
alelos do locus considerado.
O valor de He dividido pelo conjunto de loci (n) corresponde à
n
k
2
heterozigotia esperada média:
H
e
(1
l 1
p )
i 1
i
n
Tabela 1. Variação genética em alguns grupos de animais (Purves 1997).
Proporção de loci
heterozigótico
Número
de
espécies
Número
por
por
médio de
população indivíduo
loci
Invertebrados marinhos
9
26
0.587
0.147
Gastropodes marinhos
5
17
0.175
0.083
Gastropodes terrestre
5
18
0.437
0.15
Peixes
14
21
0.306
0.078
Anfíbios
11
22
0.336
0.082
Répteis
9
21
0.231
0.047
Aves
4
19
0.145
0.042
Roedores
26
26
0.202
0.054
Grandes mamíferos
4
40
0.233
0.037
Todos os grupos contêm variação genética, mas diferem na extensão dessa
variação (Tabela 1), os vertebrados são geralmente menos variáveis que os
invertebrados. Qualquer que sejam as razões que explicam o aparecimento da
6
variação genética, a maior parte das populações naturais tem variação
suficiente para que os agentes evolutivos possam actuar.
Outro tipo de comparação
resulta
do
número
de
substituições de codãos por
locus,
resultantes
de
electroforese de proteínas a
que normalmente se chama
de distância genética. Um
estudo da distância genética
média entre espécies do
mesmo
género das 5
classes
de
vertebrados,
resultou na Figura 1. Uma
das conclusões que se retira
da figura é que as aves têm
muito menos diferenciação
genética que os repteis ou
anfíbios, dentro de um
mesmo género, apesar da
grande
diferenciação
Figura 1. Distâncias genéticas e respectivas anatómica das aves. Pode
amplitudes de alguns grupos de vertebrados ser que as aves sejam
baseadas em aloenzímas (Avise, 1994).
evolutivamente mais jovens.
O número de genótipos possíveis a partir poucos loci é enorme, senão
vejamos o exemplo: com 4 alelos, temos 10 genótipos diferentes (4
homozigóticos e 6 heterozigoticos), em 100 loci pode haver 10 100 genótipos,
enquanto que em termos de frequências alélicas há um total de somente 400
(4x100).
7
ESTRUTURA GENÉTICA DAS POPULAÇÕES
Por forma a comparar genótipos diferentes e diferentes populações é
necessário existir uma medida quantitativa da variação genética. A variação
genética pode ser quantificada utilizando os conceitos de frequência alélica,
e de frequência genotípica. Enquanto as frequências genotípicas indicam
unicamente o modo de organização dos alelos em genótipos, as frequências
alélicas são a medida da variação genética. A frequência é uma proporção
relativa que varia entre 0 e 1, ou uma percentagem que varia entre 0 e 100.
Frequências alélicas
A frequência alélica num grupo de indivíduos é a proporção desse alelo
relativamente aos outros alelos desse gene. Assim, a frequência alélica pode
ser calculada a partir do número observado de diferentes genótipos num dado
locus ou a partir das frequências genotípicas. A partir do número de genótipos
contam-se o número de alelos de um dado tipo num dado locus e divide-se
pelo número total de alelos da população. Indivíduos homozigóticos possuem
duas cópias de uma mesmo alelo, enquanto que os indivíduos heterozigóticos
possuem uma cópia de alelos diferentes. Sendo p a frequência do alelo A, f(A)
e q a frequência do alelo a, o cálculo das frequências alélicas segue a fórmula:
p = f(A) = (2x número de homozigotos)+(número de heterozigotos)
(2xnúmero total de indivíduos)
Frequências genotípicas
Considerando uma população de dimensão N, contendo 2 alelos num locus,
A e a, os genótipos possíveis são AA, Aa e aa, sendo NAA, NAa e Naa os
respectivos números. Assim: N = NAA+ NAa + Naa. As frequências genotípicas
serão:
f(AA) = NAA/N ; f(Aa) = NAa/N; f(aa) = Naa/N
Sendo f(A)=p e f(a)=q as frequências alélicas de A e a, respectivamente,
então:
p = f(A)= f(AA)+ 1/2 f(Aa); q = f(a)= f(aa)+ 1/2 f(Aa)
8
Sendo HI a heterozigotia média de um indivíduos para o conjunto dos seus
loci, HS a heterozigotia de uma subpopulação com reprodução casual (=2pq) e
HT a heterozigotia do total de uma população total com reprodução casual,
podem ser definidos um conjunto de estatísticas descriptivas da estrutura
genética das populações. Os três índices F de Wright [, 1951 #880] (Caixa 2),
(Fis, FIT e FST) estão inter-relacionados da seguinte forma:
1 FIT 1 FST 1 FIS
Fis mede a redução de heterozigotia de um indivíduo devida à reprodução
não casual dentro de uma subpopulação, na realidade é o coeficiente de
consanguinidade, isto é, a proporção da variância genética de uma
subpopulação contida num indivíduo. Um valor elevado de Fis implica um
nível considerável de consanguinidade.
FIT mede a redução da heterozigotia de um indivíduo relativamente ao total
da população e reflecte o efeito da consanguinidade e deriva genética;
FST mede a redução de heterozigotia devida à deriva genética dentro de
subpopulações, reflectindo a diferenciação genética entre subpopulações,
na realidade é a proporção de variância genética de uma subpopulação (daí
o subscripto S), relativamente à variância genética total (subscripto T). Os
seus valores variam de zero a 1, sendo que um valor de FST alto
corresponde a uma diferenciação genética considerável entre populações.
FIS
HS H I
HS
FIT
HT H I
HT
FST
HT HS
HT
De qualquer forma, independentemente dos valores destes índices serem
baixos ou elevados, estes devem ser sujeitos a testes estatísticos, através
de programas de computador apropriados, como por exemplo, Genepop
[Raymond, 1995 #660] e Arlequin [Schneider, 2000 #1022].
9
CAIXA 2. F DE WRIGHT.(GENTILMENTE CEDIDA POR TEIXEIRA, S.)
10
EQUILÍBRIO DE HARDY-WEINBERG
Os modelos são descrições da natureza - verbais, gráficas ou matemáticas necessariamente incompletas. No entanto, apesar da evidente incapacidade
dos modelos em incorporar todas as variáveis de uma realidade complexa, são
utensílios que facilitam a nossa compreensão dessa realidade, permitindo
analisar de um modo compartimentado uma fracção dos processos naturais.
Um dos modelos mais utilizados em Genética de Populações é a "Lei de
Hardy-Weinberg”, que descreve o influencia da reprodução ao acaso nas
frequências alélicas e genotípicas numa população infinitamente grande. Quer
o pressuposto de população infinitamente grande, quer o de reprodução
casual, parecem irreais, mas este tipo de pressupostos são necessários de
início para simplificação da análise matemática. Começar a análise com
modelos simplistas é útil porque permite examinar o que acontece à estrutura
genética de uma dada população quando são deliberadamente violados um ou
outro ou a combinação dos pressupostos. Na realidade sabemos que tal não
acontece, mas a simplicidade algébrica e a compreensão qualitativa do modelo
de geração discreta, tornam-no particularmente acessível.1
Oócitos
Tabela 1. Quadrado de Punnet para o caso dialélico, com as frequências de
Hardy-Weinberg geradas através de reprodução casual.
Espermatozoides
p
q
f(A)
f(a)
p
f(A)
p2
AA
pq
Aa
q
f(a)
pq
Aa
q2
aa
A genética Mendeliana permite calcular as proporções numéricas da
descendência resultante do cruzamento de dois indivíduos, mas não de uma
população. A descrição da variação genética numa população é muito
simplificada quando se utilizam frequências alélicas em vez de frequências
genotípicas. Tomando como exemplo f(AA), f(Aa) e f(aa) como as frequências
genotípicas iniciais, após uma geração teremos f(AA)= p2, f(Aa) = 2pq e f(aa) =
3.
Para outros modelos que consideram a sobreposição de gerações consultar: Crow, J.F.(1986). Basic concepts in
population, quantitative and evolutionary genetics. W.H.Freeman. Cap.6
11
Frequências genotípicas
q2, como é facilmente verificável num quadrado de Punnett que represente as
frequências alélicas dos gâmetas envolvidos.
Há que reter que a probabilidade de 2 eventos independentes acontecerem
simultaneamente é calculada pelo produto das probabilidades individuais.
Sendo A e a os únicos alelos de um dado locus na população, p+q=1, ou seja,
a probabilidade de se retirar um alelo A ao acaso, mais a probabilidade de se
retirar o alelo a, contam por todos os eventos. Do mesmo modo, a soma das
probabilidades de cada genótipo também revela todos os possíveis
acontecimentos
genotípicos
e
portanto
será
igual
a
1:
2
2
p (AA)+2pq(Aa)+q (aa)=1. Assim, quaisquer que sejam as frequências
genotípicas iniciais de uma dada população do tipo acima mencionado, no
espaço de uma geração podem ser representadas por uma função binomial
(se se considerarem dois alelos) (Tabela 1) ou multinomial (se se considerarem
alelos múltiplos) das frequências alélicas e tenderão para um equilíbrio
(Roughgarden, 1979; Hedrick, 1985; Hartl e Clark, 1989; Falconer, 1989)
(Figura 2)
Figure 2. Frequências genotípicas esperadas de acordo com a hipótese de
EHW em função das frequências alélicas. Proporções de homozigóticos AA a
vermelho e aa a laranja, e de heterozigóticos Aa a azul.
Assim, se podermos determinar a frequência dos indivíduos homozigóticos
recessivos (aa) na população, a raíz quadrada dessa frequência pode ser
usada para determinar a frequência do alelo A, já que p=1-q. Conhecido p e q,
podem ser estimadas as frequências de cada genótipo. A lei de Hardy-
12
Weinberg descreve o facto de as frequências e genotípicas não se alterarão se
forem feitas determinadas assunções sobre a população.
As características genéticas de uma população são influenciadas pelo
processo de transmissão dos genes de geração em geração, pelos factores
que se mencionam seguidamente de um modo genérico (Falconer, 1989):
1. Dimensão da população
Os genes que são transmitidos de geração em geração são uma
amostra dos genes presentes na geração parental. Assim as
frequências genéticas estão sujeitas a flutuações dependentes da
dimensão da população. O polimorfismo de uma população encontrase positivamente correlacionado com a dimensão da população.
2. Diferenças na fecundidade e sobrevivência
Indivíduos com diferentes genótipos podem ter diferentes fertilidades
contribuindo de modo desigual para os gâmetas a partir dos quais irá
surgir a nova geração, pelo que as frequências alélicas serão
alteradas. Por outro lado, os genótipos dos zigotos conferir-lhes-ão
taxas de sobrevivência distintas, modificando também as frequências
alélicas da nova geração em comparação com a que lhe deu origem.
3. Migração e mutação
Fenómenos de migração de indivíduos e de mutação genética
contribuem para as alterações das frequências alélicas.
4. Reprodução
Em populações em que a reprodução é casual, populações
designadas por panmíticas, a probabilidade de cruzamento entre
indivíduos é independente da sua constituição genética (o que é
equivalente a dizer que os gâmetas masculinos e femininos se
encontram ao acaso para a formação dos zigotos), pelo que é de
esperar que as proporções genotípicas se mantenham de geração
em geração.
Em populações em que a reprodução é selectiva, como é
reconhecidamente o caso das aquaculturas, ocorrerão alterações nas
frequências genotípicas.
Em 1908, pouco depois da redescoberta dos trabalhos de Mendel, o
matemático inglês, Godfrey Hardy e o físico alemão Wilhlem Weinberg,
mostraram que existe uma relação simples entre frequências alélicas e
genotípicas. Em 1903, William Castle, geneticista americano havia já publicado
um caso especial desta relação. Com efeito, por si só, a transmissão de genes
de geração em geração não altera as frequências genotípicas características
da população acima mencionada. Esta afirmação contida na Lei enunciada por
13
Hardy (1908) e Weinberg (1908) contempla, assim populações com as
seguintes características:
1. constituídas por organismos diploides;
2. com indivíduos com reprodução sexual e casual;
3. em que as gerações não se sobrepõem;
4. com grande número de indivíduos;
5. em que a migração e mutação são negligenciáveis;
6. a selecção natural não afecta os genes em consideração.
Assim, as frequências alélicas numa população em equilíbrio H-W serão:
(A+a)2 = A2 + a2 + 2Aa, no caso binomial e
(A+a+a’+a’’+...)2 = A2 + a2 + a’2 + a’’2+2Aa+2Aa’ +2Aa’’+2aa’+2aa’’+2a’a’’+..., no
caso polinomial
Ainda que, na realidade, as populações não sejam infinitas nem totalmente
panmíticas, a distribuição dos genótipos observados é raramente diferente da
distribuição teórica prevista pela Lei de HARDY-WEINBERG (salvo em casos
particulares, como nos moluscos, que são hermafroditas e podem
autofecundar-se) [Agnèse, 1989 #8].
Este modelo tão simples é fundamental da genética de populações, pois
permite comparar frequências alélicas observadas com as esperadas e atribuir
os desvios a fenómenos de mutação, selecção, reprodução ou migração
preferenciais, isto é, que atingem em especial determinado grupo ou grupos
dentro da população ou espécie estudadas.
O Equilíbrio de Hardy-Weinberg (EHW) permite-nos, pois, inferir de desvios
das frequências observadas relativamente às esperadas e especular quanto às
razões desses desvios. Quando as premissas assumidas sobre a população
não se verificam, esses desvio podem ser devidos a:
1. População de dimensões pequenas - se a população é pequena, erros de
amostragem podem causar alterações imprevisíveis nas frequências
alélicas, que por si são independentes de outros factores actuando sobre a
população. Ao longo do tempo, este erro de amostragem (deriva genética)
pode conduzir à fixação de um dos alelos.
2. Desvios à reprodução é casual - significa que alguns cruzamentos ocorrem a
frequências diferentes das preditas com base nas frequências genotípicas
da população. Há vários tipos de desvios e estes podem ter consequências
diferentes na população:
cruzamento entre indivíduos fenotípica ou genotipicamente similares
aumenta a homozigotia nos loci envolvidos, sem alteração das
frequências alélicas;
14
cruzamento entre indivíduos fenotípica ou genotipicamente
dissimilares aumenta a heterozigotia nos loci envolvidos, sem
alteração das frequências alélicas;
cruzamento dependente da densidade aumenta, em geral, a
frequência de alelos raros, aumentando a heterozigotia;
cruzamento entre indivíduos relacionados aumenta a homozigotia
sem afectar as frequências alélicas.
3. Mutação, migração e selecção, cujos efeitos serão apreciados em detalhe
mais adiante.
Para que se possa atribuir significado estatístico, devemos testar esse
desvio. Os testes actualmente disponíveis constam de variações do teste 2,
para os casos de amostras de pequenas dimensões em que são necessários
mecanismos de correcção, uma vez que os resultados do teste 2 em casos
em que a dimensão da amostra seja pequena (N <50) devem ser interpretados
com precaução e em que a dimensão das classes genotípicas esperadas é
menor que 5. Actualmente o teste mais utilizado é o teste exacto de Fisher
(Raymond and Rousset 1995a) implementado no programa Genepop
(Raymond and Rousset 1995b).
15
Caixa 3. Teste equilíbrio Hardy-Weinberg
Foram analisados indivíduos com os seguintes genótipos: 10 AA, 190 Aa e 50 aa, para se poder
apreciar avaliar a hipótese nula (H0) de a população se encontrar em equilibrio de HardyWeinberg. O procedimento é o seguinte:
Passo 1: Cálculo das frequências alélicas
10+190+50 = 250 indivíduos no total.
250 x 2 alelos por indivíduos = 500 alelos no total.
Frequência alelo p (fA) = 10 homozigoticos x 2 alelos cada + 190 heterozigoticos x 1 alelo =
210 500 alelos = 0.42.
Frequência alelo q (fa) = 50 homozigoticos x 2 alelos cada + 190 heterozigoticos x 1 alelo =
290 500 alelos = 0.58.
Passo 2: Cálculo das frequências genotípicas, usando o modelo Hardy-Weinberg
(p + q)2 = p2 + 2pq + q2
p2 = FAA = 0.422 = 0.1764
2pq = FAa = 2 x (0.42)(0.58) = 0.4872
q2 = Faa =0.582= 0.3364.
Passo 3: Cálculo do número esperado de indivíduos de cada genótipo
O número esperado de indivíduos de cada genótipo é calculado multiplicando a frequência
esperada de cada genótipo pelo total de indivíduos da amostra.
Número esperado de indivíduos AA = 0.1764 × 250 = 44.1
Número esperado de indivíduos Aa = 0.4872 × 250 = 121.8
Número esperado de indivíduos aa = 0.3364 × 250 = 84.1
Passo 4: Teste 2 para avalação da hipótese nula
O teste 2 é usado para determinar se o número observado de indivíduos de cada genótipo
estão em conformidade com o esperado pelo EWH.
2 = (observed number – expected number)2/expected number.
For AA, 2 = (10 – 44.1)2/44.1 = 26.37.
For Aa, 2 = (190 – 121.8)2/121.8 = 38.19.
For aa, 2 = (50 – 84.1)2/84.1 = 13.83.
= 78.39
Os graus de liberdade associados a este valor de 2 são: número de classes (genótipos), neste
caso 3, menos 1, menos o número de parâmetros estimados nos dados, neste caso, p foi
estimado a partir dos dados. Uma vez conhecido p, sabe-se q, q = 1 – p. Assim, os g.l.= 3 – 1 –
1 = 1. Com um grau de liberdade o valor de 2 de 78.39 é altamente significativo(p < 0.0001).
Concluimos, assim, que as frequências genotípicas observadas não estão de acordo com o
esperado conforme o EWH e pelo menos uma das premissas terá sido violada.
16
DERIVA GENÉTICA
Sucessivas gerações são o resultado de uma amostragem ao acaso do pool
genético parental. Imagine-se uma população de 10 indivíduos, dos quais 3
têm o genótipo AA, 4 Aa e 3 aa. A população tem pois 10 alelos A e 10 alelos
a, ou seja a frequência de cada alelo é 0.5. Na ausência de factores como a
selecção e mutação, será de esperar que na próxima geração as frequências
se mantenham. Mas as frequências alélicas poderão por casualidade serem
diferentes das da geração anterior por simples amostragem.
A amostragem as acaso inicia-se no momento da formação do zigoto. Em
cada espécie, cada indivíduo produz muito mais gâmetas do que aqueles que
irão ser fertilizados. Os gâmetas que irão dar origem a indivíduos representam
somente uma amostra dos muitos gâmetas que são produzidos pela geração
parental (Figura 3). Se o progenitor é homozigótico, a amostragem não afecta
a descendência, já que todos os gâmetas contêm o mesmo alelo. No entanto
se fôr heterozigótico, a proporção de gâmetas com o alelo A e com o alelo a,
será aproximadamente 50%. As proporções não serão exactamente 0.5 já que
as células reprodutivas podem morrer antes da formação dos gâmetas, ou
porque por exemplo ¾ dos produtos da meiose são perdidos como corpos
polares. Se um progenitor heterozigótico produzir 10 descendentes, pode ser
que 5 tenham herdado o gene A e 5 o gene a, ou 6 herdem o gene A e 4 o
gene a.
Geração parental
Geração
F (brancos)
0
0.5
0.5
Pool gamético
Geração parental
1
0.7
Pool gamético
Geração parental
3
0.8
0.8
Pool gamético
Geração parental
0.7
Figura 3. Efeito da amostragem
casual de gâmetas de geração
em geração.
Laurent Excoffier
(http://anthropologie.unige.ch/
evolution/default.htm)
4
0.4
17
Frequência
alélica
O acaso contribui assim para a modificação das frequências alélicas, uma vez
que a amostragem de gâmetas de geração em geração é um processo por ele
directamente afectado (Figura 4). Isto é, o facto de somente uma parte dos
gâmetas produzidos ir contribuir para a geração seguinte, admitindo que esses
gâmetas têm um valor selectivo idêntico constitui um processo casual.
Às flutuações de frequências alélicas que podem levar à fixação de um ou
outro alelo independentemente do seu valor adaptativo, dá-se o nome de
deriva genética (Hartl and Clark 1997). As alterações de frequências alélicas
devidas à deriva genética são erráticas em qualquer população e embora a sua
previsão seja quase impossível, é possível prever o comportamento médio dos
alelos em grandes populações.
N=10
N=10
N=20
N=20
Gerações
Figura 4. Simulação do efeito da deriva genética em populações pequenas, tal
como são as stocks de progenitores utilizados em aquacultura. Em programas
de melhoramento genético, para se conseguirem os objectivos é necessário
frequentemente descentes de determinada geração como progenitores da
seguinte. Os efeitos dessa acção podem ser drásticos em poucas
goikoikerações com o desaparecimento de alelos em muito poucas gerações.
Gráficos gerados a partir do programa Populus 5.2.1 (Alstad et al. 2002).
Uma vez que todas as populações têm uma localização geográfica ou
condições ambientais definidas, a diferenciação genotípica devida ao acaso
constitui a regra. No entanto, tal poderá vir a ter um impacto menos importante
no total da população, uma vez que as oportunidades de reprodução e/ou
sucesso para cada subpopulação serão também elas distribuídas ao acaso
entre as subpopulações. Esse facto assegura que, enquanto cada
subpopulação terá a sua própria evolução de frequências alélicas, qualquer
18
efeito cumulativo na população total será de natureza estocástica (Fredeen
1986).
Resumindo, os efeitos da deriva genética são (Weaver and Hedrick 1989):
Fixação ou perda de um dos alelos;
A frequência média dos alelos não se altera no conjunto das
populações, mas a sua distribuição modifica-se.
Um dos modos de avaliar a deriva genética numa geração é calcular a
variância da frequência alélica no conjunto das populações (porque a deriva é
o "erro" de amostragem dos gâmetas que irão constituir a próxima geração):
V= pq/2N, sendo p e q as frequências dos alelos e N o efectivo da população.
Daí o facto de a contribuição do acaso para modificar as frequências alélicas
esteja inversamente relacionada com a dimensão da população (Fredeen
1986; Weaver and Hedrick 1989).
Quando as populações sofrem uma diminuição brusca do seu efectivo
("bottleneck" ou gargalo) ou quando uma população coloniza novos territórios
com um pequeno número de efectivos (efeito fundador), o papel
desempenhado pela deriva genética é de importância particular na alteração
de frequências alélicas e no perfil genético das futuras gerações porque o
número de indivíduos da recente população é naturalmente menor que o da
população original, potenciando o efeito da deriva genética (Figura 5). Este
efeito em aquacultura é observável na constituição do stock de progenitores,
que constitui uma amostra ínfima da população natural.
Figura 5. Efeito fundador constitui outro aspecto
da amostragem aleatória de alelos para formar
uma nova população. Neste caso amostragem
aleatória é a dos indivíduos migradores que vão
formar a nova colónia, durante a mesma
geração. O efeito fundador tem consequências
devastadoras sobre as frequências alélicas tanto
mais quanto menor fôr o número de indivíduos
migradores.
Laurent Excoffier (http://anthropologie.unige.ch/evolution/default.htm)
Se duas populações, em proporções de Hardy-Weinberg, com diferentes
frequências alélicas forem juntas, a população total terá uma frequência alélica
19
igual à média das frequências nas duas populações. Os efeitos desse tipo de
aglomeração devem ser considerados como complicações potenciais para a
análise genética, porque a subdivisão não reconhecida pode ocorrer em
amostras de virtualmente todas as populações naturais. Após uma geração de
reprodução ao acaso, resultará em proporções H-W para os genótipos, mas as
frequências de homozigóticos deverá ser mais pequena que a média das
frequências de homozigóticos nas duas subpopulações iniciais. Esta redução
de homozigotia é chamada de Efeito de Wahlund.
De modo a compreender o efeito de Wahlund, imagine duas subpopulações
(1 e 2) isoladas com o alelo a, em que f(a1)= q1 e f(a2)= q2. Qual é a frequência
média de homozigóticos nas duas subpopulações e no conjunto destas?
AA
p12
Pop 1
p22
Pop 2
Pop 1 + Pop (p12 + p22)/2
2
Aa
2 p 1 q1
2 p 2 q2
p1 q1 + p2 q2
aa
q12
q22
(q12 + q22)/2
Tomemos o exemplo prático de uma população que tem uma frequência de
albinismo de 16% e uma outra população próxima em que essa mutação não
está presente. Qual a frequência total de albinos no conjunto das duas
populações? (0.16+0)/2=0.08. Qual a frequência alélica da mutação numa
população resultante da fusão das duas populações anteriores e em que existe
panmixia? (p1+p2)/2=(0.16 + 0)/2 = 0.2. Qual a frequência de homozigóticos
recessivos na nova população? 0.22=0.4. Ou seja, a frequência de albinos na
nova população é menor que a frequência média desses indivíduos nas duas
populações anteriores.
20
DIMENSÃO EFECTIVA DA POPULAÇÃO
A forma mais conveniente de lidar com os desvios da panmixia é
expressar a situação em termos de número efectivo de indivíduos que
contribuem efectivamente para a próxima geração, que se denomina
simplesmente por dimensão efectiva da população, Ne. Na realidade existem
indivíduos que, por vários motivos, nao se reproduzem, e que portanto, não
transmitem os seus genes à geração seguinte, pelo que em termos genéticos,
é como se não existissem. Daí que a definição de dimensão efectiva da
população seja: o número de indivíduos que experimenta os efeito da deriva
genética e da consanguinidade à mesma taxa da população real. Importa
analisar brevemente 2 situações principais em que o número de indivíduos da
população e a dimensão efectiva da população diferem, mas que se podem
relacionar, a saber:
i) sex ratio (proporção entre sexos),
Ne
4Nm Nf
N m Nf
Em que Nm é número de machos e Nf o
número de fêmeas. É óbvia a
constatação de que Ne será tanto mais
maior, quanto mais próximo de 1 forem
as proporções entre os 2 sexos.
Dimensão efectiva da população
)
Se um dos sexos fôr mais raro, o número de indivíduos desse sexo dominará
as alterações de frequências alélicas. É mais provável que genes idênticos
sejam provenientes de indivíduos desse sexo, porque são menos os
indivíduos contribuem para a próxima geração. Assim sendo, a dimensão
efectiva da população será (Figura 6):
250 machos
500
400
300
100 machos
200
50 machos
100
25 machos
Figura
6.
Dimensão
efectiva da
população resultante do cruzamento de
10 machos
2 machos
várias combinações do número de
0
1 machos
0
50
100
150
200
250
machos e fêmas. A dimensão efectiva foi
Number of fêmeas
calculada
com
base
em
dois
pressupostos: reprodução casual e todos os progenitores contribuem
igualmente para a próxima geração. Traduzido de Tave (1993).
ii) flutuações populacionais,
21
Quer nas populações naturais quer nos programas de melhormento genético, é
relativamente fácil existirem flutuações no número de progenitores utilizados. A
relação entre dimensão efectiva da população e as flutuações populacionais
pode ser descrita da seguinte forma:
1 1 1
1
1
Ne t Ne1 Ne 2
Net
em que Nex é dimensão efectiva da população na geração x.
Num caso extremo, em que uma das famílias sofre um diminuição drástica do
número de indivíduos, o efeito na dimensão efectiva da população é também
muito forte (Figura 7).
Geração
1
2
Família 1
100
100
100 100 100
Família 2
100
5
100 100 100
Média
Família 1
Família 2
100
81
3
N
4
e
100
20.8
5
DF
0.005
0.024
Figura 7. Exemplo da influência da flutuação do número de indivíduos sobre a
dimensão efectiva da população. De notar a comparação entre a média
aritmética (81) e a média harmónica que corresponde à dimensão efectiva da
população (20.8).
A diminuição de Ne pode ter resultados muito negativos entre a quais a
redução da productividade e o aumento da incidência de anomalias de
desenvolvimento.
22
CONSANGUINIDADE
Entende-se por consanguinidade a reprodução de organismos que se
encontram relacionados entre si através de ancestrais. A relação entre os
indivíduos depende logicamente da dimensão da população, considerando o
número possível de antepassados. Numa população de organismos bissexuais
cada organismo tem 2 pais, 4 avós, 8 bisavós etc. de modo que em t gerações
terá 2t antepassados. Se recuarmos o suficiente, o número de antepassados
necessário que todos os indivíduos tenham, no presente, antepassados
diferentes, é superior ao de qualquer população real. Assim qualquer par de
indivíduos estará relacionado entre si, através de um ou mais antepassados
comuns num passado mais ou menos longínquo. Quanto mais pequena fôr a
população em gerações anteriores, menos longe estarão os antepassados
comuns, ou maior será o seu número. Assim, numa pequena população a
probabilidade de dois indivíduos se encontrarem ligados por antepassados
comuns é superior do que numa população maior. Esta é a razão pela qual as
propriedades de populações pequenas são tratadas como consequências da
consanguinidade.
Se dois indivíduos possuem um alelo igual devido a esse alelo ter sido
transmitido por antepassados comuns, diz-se que são idênticos (para esse
alelo) por descendência (IPD) ou, homozigóticos idênticos. De facto, há
também a hipótese de esse alelo ser igual por evolução comum e neste caso
designa-se por não idêntico por descendência (NIDP) (Figura 8).
NIPD
IPD
Figura 8. Esquema ilustrativo da possibilidade de 2 indivíduos terem uma
constituição genotípica igual, embora com consanguinidades distintas. Um dos
indivíduos recebe ambos os alelos de um ancestral, enquanto que no outro um
dos alelos vem de um indivíduos não aparentado.
23
O coeficiente de consanguinidade (F) é baseado na probabilidade de dois
alelos de um mesmo locus serem iguais no mesmo indivíduo, e expressa o
grau de relacionamento entre os progenitores desse indivíduo. Se a geração
parental se reproduz ao acaso, então o coeficiente de consanguinidade é a
probabilidade de dois gâmetas tirados ao acaso da geração parental tenham
alelos idênticos num dado locus. O coeficiente de consanguinidade é um valor
relativo de comparação entre duas populações, em que se especifica um
determinado tempo no passado em que consideramos todos os alelos da
população independentes. Este ponto é a população base que por definição
tem um F=0 e mesmo que não se explicite a referência a esta população é
dela que sempre se parte.
Consanguinidade na população ideal
O cálculo do coeficiente de consanguinidade pode ser pensado para uma
população de hermafroditas marinhos, capaz de autofertilização, lançando
ovócitos e esperma para o mar. Há um total de Ne indivíduos, cada produzindo
um número idêntico de gâmetas que se fertilizam ao acaso. Todos os genes da
população se consideram não idênticos (alelo transmitido por antepassados
não comuns). A probabilidade de um par de gâmetas terem genes idênticos é
designada por coeficiente de consanguinidade.
Figura 9. Relação entre o nível de
consanguinidade por geração e a
dimensão efectiva da população.
Traduzido de Tave (1993).
consanguinidade / geração (%)
A relação inversa entre F e Ne indica claramente que a uma diminuição de Ne
corresponde um aumento de F (Figura 9). Isto acontece porque muito
simplesmente num conjunto menor de indivíduos em condições de se
reproduzirem será mais provável que pelo simples acaso, gâmetas de
indivíduos com algum grau de parentesco se conjunguem.
50
40
30
20
10
1
10
100
1000
Ne
Na primeira geração será a probabilidade de os gâmetas terem sido
produzidos pelo mesmo indivíduo: 1/2Ne. Na segunda geração há dois modos
de surgirem homozigoticos idênticos:
24
os gâmetas terem sido produzidos pelo mesmo indivíduo da geração 0
(1/2Ne);
os restantes gâmetas não são idênticos na sua origem na geração 1
(probabilidade 1-1/2Ne) dos gâmetas que não, mas que podem ser
idênticos na geração 0. A probabilidade de origem idêntica na geração 0
é o que já determinámos como F1. Assim, a probabilidade total de serem
produzidos homozigoticos idênticos na geração 2 é: F2= (1/2Ne)+[1(1/2Ne)F1].
Geração 0
Geração 1
Geração 2
Geração 3
Geração t
F de cada geração
F0 = 0
F1 = 1/2Ne
F2 = 1/2Ne
F3 = 1/2Ne
Ft = 1/2Ne
F Total
0
(1/2Ne)
1/2Ne+(1-1/2Ne)F1
1/2Ne+(1-1/2Ne)F2
1/2Ne+(1-1/2Ne)Ft-1
A consanguinidade é pois composta de 2 partes: um incremento de 1/2Ne,
atribuível a reprodução dos indivíduos produzidos na geração anterior, e um
resíduo resultante da consanguinidade anterior e tendo a consanguinidade da
geração anterior.
Se quisermos conhecer FX:
B
A
P
C
Q
X
Os progenitores, P e Q, encontram-se relacionados através de A e só temos
de considerar a transmissão dos genes de A através de P e Q até X e calcular
a probabilidade de X ser homozigotico idêntico. Sendo A1 e A2 os alelos de A
num determinado locus, a probabilidade de X ser A1A1 é, (1/2)4 = 1/16, porque
a probabilidade de A1 ser transmitida através de cada uma das 4 vias AP, PX,
AQ e QX é de 1/2 para cada. A probabilidade de X ser A2A2 é, (1/2)4 e a
probabilidade de X ser ou A1A2 ou A2A1 é, (1/2)4 x 2 = 1/8.
Esta probabilidade de X ser um homozigoto idêntico representa uma
consanguinidade surgida a partir de A, se no entanto, A fôr ele próprio
homozigoto idêntico através de consanguinidade prévia, X será um homozigoto
idêntico mesmo que tenha como genótipo A1A2 ou A2A1 (distinguindo-se pelo
facto de A1 vir de P ou Q).
25
A probabilidade de A ser um homozigoto idêntico é o seu coeficiente de
consanguinidade F1. A probabilidade adicional de X ser um homozigoto
idêntico através de consanguinidade prévia é (1/2)3*FA. Adicionando ambas as
probabilidades, temos o Coeficiente de consanguinidade:
FX = (1/2)3+(1/2)3*FA = (1/2)3*(1+FA)
A fórmula geral é FX = (1/2)n*(1+FA), em que n é o número de indivíduos
em qualquer "path", contando os parentes de X, o ancestral comum e todos os
indivíduos que ligam o ancestral comum aos parentes de X.
Há ainda outro modo de calcular os coeficientes de consanguinidade. Na
realidade é um método utilizado para planeamento de cruzamentos que
resultem num mínimo de consanguinidade e para calcular o coeficiente de
geração a geração numa população conhecida. Os métodos não diferem em
princípio da fórmula geral anteriormente apresentada, mas em vez de se
trabalhar do presente para o passado até ao ancestral comum, trabalhamos
para o futuro, calculando a consanguinidade de cruzamentos que se realizam
no presente. O coeficiente de consanguinidade de um indivíduo depende da
quantidade de ancestrais comuns dos dois parentes. Assim, em vez de se
pensar na consanguinidade da prole, podemos pensar no grau de relação por
descendentes entre 2 parentes (f). O f dos parentes é equivalente ao
coeficiente de consanguinidade da prole se esta se reproduzisse, assim é a
probabilidade de 2 gâmetas escolhidos ao acaso, um de cada indivíduo,
possuírem alelos idênticos por descendência. Assim para o exemplo acima
exposto, se tirarmos um gâmeta de P ao acaso, e um de Q ao acaso, e
repetirmos o procedimento muitas vezes, em metade dos casos o gâmeta de P
terá um gene de A e noutra metade terá um de B, e o mesmo acontecerá para
Q (1/2 B, 1/2 C). Assim, os 2 gâmetas um de P e outro de Q, terão os genes de
A e B, B e C, A e C e só de A, 1/4 das vezes.
26
MUTAÇÃO
A mutação é um processo particularmente importante em genética de
populações, uma vez que constitui a fonte principal de variação genética em
espécies ou populações. A mutação pode envolver somente uma base de
DNA, várias bases, parte do cromossoma ou de vários cromossomas. A causa
imediata de uma mutação pode ser um erro na replicação do DNA, uma
quebra física do cromossoma, a inserção de um elemento ou a falha de
disjunção na meiose.
Em genética de populações interessam sobretudo as mutações
espontâneas. Analisemos então o efeito da mutação na variação genética
numa população, assumindo que a taxa de mutação (proporção de alelos que
mutam) do alelo selvagem A em B, por gâmeta por geração, é u; e que a taxa
da mutação inversa, B em A, é v. Porque só os alelos A podem mutar para B, e
o alelo A tem uma frequência p, o aumento de frequência de B (q) será de up.
Do mesmo modo, a frequência de B decrescerá de vq. No conjunto a alteração
de frequência de A (delta p) e de B (delta q), devido exclusivamente às
mutações é de:
u
A (p)
(q) B
v
delta p = -up+vq
delta q = up-vq
É fácil de ver que esta situação conduzirá a um equilíbrio das frequências
alélicas. Porque se a frequência de um alelo aumentar (por exemplo A), menor
será a frequência do outro (B) e menos mutações se verificam na direcção de
A. O ponto de equilíbrio será:
pu = qv => p/q = v/u => q = u/(u+v)
O modo como as frequências alélicas convergem para o equilíbrio é
mostrado na figura 10 (pág.113 Hartl). De notar que, qualquer que seja a
frequência inicial de A, a sua frequência alélica atingirá sempre o equilíbrio. No
entanto, como as taxas de mutação são geralmente muito pequenas, entre 10 4 e 10-6, o que significa que entre 1 gâmeta em 10.000 a 1 em 1.000.000 tem
um novo alelo mutante, pelo que as alterações de frequência devidas à
27
mutação são negligíveis, no espaço de algumas gerações, embora o seu papel
à escala de tempo evolutiva seja relevante. Geralmente são necessários
milhares ou dezenas de milhar de gerações para que se atinja um equilíbrio. A
mutação conjuntamente com a deriva genética proporcionam uma explicação
razoável para a quantidade de variação genética observada em muitas
espécies.
O estudo do equilíbrio entre as mutações nas duas direcções foi efectuado,
tendo sido mostrado que as mutações no sentido inverso (mutante >
selvagem) são geralmente muito menos frequentes.
Figura 10. A alteração
de frequências do
alelo
A
como
resultado da mutação
de A em a, a uma taxa
constante (=10-5).
Número de gerações
28
MIGRAÇÃO
Ao movimento de indivíduos entre populações dá-se o nome de migração. A
migração pode afectar as frequências alélicas das populações envolvidas, se
existirem diferenças entre as frequências alélicas dos indivíduos que migram e
a população que os recebe. A migração pode suavizar os efeitos de perda de
diversidade genética devida à deriva genética (contribuindo com novos alelos
ou alelos raros para a população recipiente) e inbreeding e ainda impedindo a
diferenciação genética pelas mesmas razões. Em aquacultura, os indivíduos
encontram-se confinados pelo que a migração como fenómeno natural não
existe. No entanto, a entrada de novos indivíduos para o stock de reprodutores
terá as mesmas consequências que uma migração.
Uma espécie raramente consiste numa única e grande população
panmíctica, ocorrendo mais vulgarmente em várias subpopulações separadas
geográfica ou temporalmente. Assim sendo, porque é que as subpopulações
que se encontram divididas não fixam determinados alelos, como com o que
se passa em casos de consanguinidade? Na realidade, as populações não
estão completamente isoladas, havendo um certo número de indivíduos que
migram de uma a outra, fazendo com que hajam trocas genéticas (fluxo
genético).
Se houver um grande número de migradores entre as duas populações, o
efeito será o de integrar as duas populações numa única população
panmíctica, pelo que haverá grande variação genética na população total. O
outro extremo será o isolamento completo das subpopulações, em que haverá
menos variação intrapopulacional, mas grande divergência interpopulacional.
A distribuição da variação genética intraespecífica depende da dimensão
das subpopulações locais, o tempo de isolamento e a quantidade de indivíduos
migradores que ocorrem, relativamente ao total da população.
A deriva genética reduz a variação genética nas populações pequenas, pelo
que quanto menor fôr a subpopulação, menor será a variação genética que
conseguirão manter. Quanto mais tempo as subpopulações estiverem
isoladas, mais tempo terão tido para acumular diferenças genéticas. Quanto
menor forem as trocas genéticas interpopulações, menos serão as
semelhanças a nível genético. Todos estes factores interagem na distribuição
da variação genética dentro de uma espécie.
Gyllensten (1985) comparou a distribuição da variação genética
intraespecífica para 19 espécies de peixes e conclui que: a variação genética
intraespecífica é superior nas espécies marinhas do que nas espécies
dulçaquícolas; uma proporção superior de variação intraespecífica, no caso de
29
espécies de água doce, é devida a diferenças genéticas entre localidades. As
espécies anádromas são intermédias entre a situação das espécies marinhas
e dulçaquícolas, para ambos os casos. Gyllensten concluiu que estas
diferenças resultam principalmente do facto de que nas espécies marinhas as
populações têm dimensões superiores e taxas de migração mais elevadas.
Uma grande variedade de modelos de migração foram criados de modo a
serem considerados os efeitos da subdivisão de populações em
subpopulações semi-isoladas (demes) com vários padrões de trocas genéticas
ou de migração. Os efeitos combinados de selecção e migração têm sido
examinados e alguns dos modelos predizem clines geográficos das
frequências alélicas tal como ocorre frequentemente no mundo natural. Um
cline geográfico de frequências alélicas é caracterizado por um aumento ou
diminuição constantes da frequência alélica ao longo de uma dada região
geográfica. Os efeitos da migração entre demes semi-isolados pode ser um
factor importante na evolução adaptativa quando combinado com efeitos de
selecção natural e deriva genética que ocorrem em cada deme.
O efeito da migração pode ser descrito do seguinte modo: suponhamos que
uma grande população consiste de uma proporção m de migradores, sendo o
restante 1-m, nativos. Se a frequência de uma dado alelo fôr q1 nos nativos e
q2 nos migradores, na população total qual será a frequência de q?
q= mq2 + (1-m) q1 = mq2 + q1 - mq1 = m(q2 - q1) + q1
Após uma geração de imigração, q será igual à diferença de frequências
antes (q0) e depois da imigração (q1):
q = q1 - q0 = m(q - q0) + q0- q0
q2 Pop2
p2
q1 Pop1
p1
q = m(q - q0)
1-m
Pop 1 + Pop 2
m
Portanto a taxa de alteração
(1- m)q1 +mq2
das frequências genéticas de
uma
população
sujeita
à
migração depende obviamente da
taxa de imigração e da diferença das frequências alélicas entre imigrantes e
nativos. Se m=0 ou q1 = q0 não haverá alteração nas frequências .
30
31
SELECÇÃO
O teorema da evolução através da selecção natural é baseado nas
seguintes premissas:
1. As espécies têm mais descendentes do que aqueles que podem
sobreviver e reproduzir-se;
2. Diferentes organismos têm diferentes capacidades de sobreviver e
reproduzir-se (reprodução diferencial);
3. Parte da variação na capacidade de sobrevivência e reprodução é
hereditária.
Estas premissas traduzem-se, na prática, no facto de certos genótipos
estarem mais adaptados a um dado ambiente que outros (maior ”fitness”maior capacidade de sobrevivência e reprodução num dado ambiente)
deixando, assim, mais descendência apta a sobreviver e ao longo do tempo, as
frequências alélicas modificam-se de modo a que a população está cada vez
mais adaptada. (A selecção natural é fruto da eficácia reprodutiva diferencial
dos distintos genótipos como consequência do seu grau de adaptação ao
ambiente).
O número provável de descendentes de cada genótipo na geração seguinte
é a expressão do seu valor adaptativo. A selecção é a medida da diferença
entre a frequência relativa dos descendentes prevista pela lei de HardyWeinberg e a frequência observada.
A selecção pode pois ocorrer de vários modos afectando, como se referiu a
fertilidade ou o sucesso reprodutivo. A selecção tem dois efeitos básicos na
variação genética:
1. quando favorece um alelo em particular pode conduzir à redução da
variação genética e, consequentemente, à homozigotia do alelo
favorecido;
2. quando não favorece um alelo em particular, pode manter a presença
de 2 ou mais alelos na população.
De modo a se compreenderem os efeitos da selecção na variação genética,
devemos considerar o 'fitness' dos diferentes genótipos. O 'fitness' pode ser
definido como a capacidade de os diferentes genótipos passarem alelos às
gerações futuras. Geralmente o valor mais alto do 'fitness'‚ 1.0, sendo todos
os outros valores tomados em referência a este, pelo que‚ na realidade um
'fitness' relativo embora o passaremos a designar somente como 'fitness'.
32
Apesar da complexidade da determinação do 'fitness', podemos explorar as
consequências da selecção com a ajuda do modelo de Hardy-Weinberg,
assumindo:
Organismo diploide.
Reprodução sexual.
Gerações não sobrepostas.
População de dimensão infinita.
Reprodução ao acaso.
Ausência de migração.
Ausência de mutação.
Ocorrência de selecção, 'fitnesses' constantes e iguais entre sexos.
Geração Estádio no
ciclo de vida
Frequências
t
Gâmetas
A
t+1
Genótipos
AA
Aa
aa
Freq. genótipos (zig.)
p2
2pq
q2
Fitness
Genótipos adultos
Gâmetas
WAA
p2 WAA
A
WAa
Waa
2pq WAa q2 Waa
a
t+1
Freq. gaméticas
a
p2 WAA +(1/2)(2pq WAa) = p(p WAA+q WAa)
q2 Waa +(1/2)(2pq WAa) = q(p WAa+q Waa)
Fitness médio
W = p(p WAA +q WAa) + q(p WAa+q
Waa)=
= p2 WAA+2pq WAa+q2 Waa
Freq. gaméticas
Freq. alélicas
A
a
p'= p(p WAA+q WAa)/W
q' = q(p WAa+q Waa)/W
Dp = p'-p =
= pq [p( WAA - WAa)+q( WAa - Waa)]/W
Selecção contra um dos homozigotos
Consideremos a situação em que a selecção opera contra um dos
homozigotos, tendo o outro homozigoto e o heterozigoto 'fitnesses' iguais. Se o
'fitness' dos genótipos AA, Aa e aa fôr, respectivamente, 1, 1 e 1-s (sendo s a
33
desvantagem selectiva ou coeficiente de selecção), podemos prever, na
ausência de outros factores susceptíveis de induzir alterações nas frequências
alélicas, qual a evolução das frequências alélicas e genotípicas. A contribuição
dos três genótipos para a geração seguinte‚ produto da frequência dos
genótipos antes da selecção, pelo seu fitness. Assim se s=1, então o alelo a‚
letal, pelo que a frequência de a baixar consideravelmente, desaparecendo o
genótipo aa. Uma vez que estamos a considerar somente a selecção
resultante de diferentes viabilidades dos genótipos, o 'fitness' ser a
probabilidade relativa de sobrevivência do zigoto até, à reprodução.
O fitness relativo de AA, Aa e aa é, respectivamente, WAA , WAa e Waa.,
sendo WAA =1, WAa =1 e Waa = 1-s. Para simplificar, comecemos por substituir
a designação das frequências alélicas: FA2 por p2, 2 FA Fa por 2pq e Fa2 por q2.
A frequência de cada genótipo será igual à sua frequência inicial multiplicada
pelo seu valor adaptativo: p2 1 : 2 pq 1 : q2 (1-s), em relação ao efectivo total da
população. O 'fitness' médio da população, equivale ao efectivo total da
população após uma geração submetida à selecção, passa de 1 a:
W = p2 (1) + 2pq (1) + q2 (1-s)=
= p2 + 2pq + q2 - q2s=
= 1 - q2s
Podemos esquematizar as frequências dos genótipos antes e depois da
selecção, do seguinte modo:
Coeficiente de selecção
Fitness relativo
Frequência inicial
Frequência depois da selecção
Total
AA
0
1
p2
p2
Aa
0
1
2pq
2pq
aa
s
1-s
q2
q2 (1s)
1-sq2
E assim, numa geração, com o efeito da selecção, as frequências alélicas
de A mudam de:
p a p (t+1) = (p2 +pq)/(1-q 2 s)= p(p + q )/ 1-q 2 s
q a q(t+1)
= pq+q2(1-s) / 1-q 2 s = pq+q2-q2s/1-q 2 s =
=q [p + q -qs)]/1-q 2 s = q(1-qs)]/ 1-q 2 s
34
Portanto a frequência de um alelo após selecção é função da frequência
antes da selecção e do coeficiente de selecção.
A alteração da frequência alélica numa geração devida à selecção é definida
por: q=q’-q:
q=q’-q=
q 2 1 s pq
1 q2s
q=
q 2 q 2 s pq q q 3 s
1 q2s
= q
q qs q 2 s
1 q2s
2
=
q 2 q 2 s pq q 1 q 2 s
1 q2s
=
q q qs p 1 q 2 s
=
s q 3s
1 q2s
1 q2s
q 2 s1 q q 2sp
=
=
1 q 2s
1 q2s
Neste caso, a alteração de frequência é negativa, pelo que a selecção
reduzirá a frequência de a.
p=p’- p=
p 2 pq
1 q2s
p=
p 2 pq p 1 q 2 s
1 q2s
p 2 pq p pq 2 s
=
1 q2s
p p q 1 q s
p p q 1 q2s
1 q2s
2
=
1 q2s
=
pq 2 s
=
1 q2s
Para diferentes frequências iniciais, com um coeficiente de selecção
constantte (0.2), q varia numa geração tal como o indicado na figura (Figura
11). A alteração é nula, quando p ou q são zero, uma vez que a população é
monomórfica para a ou A, respectivamente; é maior quando as frequências
alélicas são intermédias e é menor quando q se aproxima de zero, uma vez
que a maior parte dos alelos a estão presentes nos indivíduos heterozigotos e
portanto não estão sujeitos à selecção.
A selecção aqui descrita conduz à eventual fixação de um alelo e como
resultado reduz a variação genética na população. No entanto, quando os
heterozigotos têm uma vantagem selectiva (fitness maior), os dois alelos
podem ser mantidos na população.
35
REFERÊNCIAS
Alstad, D., A. Anderson, L. Roe, S. Noorbaloochi, and C. Bratteli. 2002.
Populus: simulations of population biology, University of Minnesotta.
Beaumont, A. R., and K. Hoare. 2003. Biotechnology and Genetics in Fisheries
and Aquaculture
Cavalli-Sforza, L. L., and W. F. Bodmer. 1971. The genetics of human
populations. W. H. Freeman, San Francisco.
Dunham, R. A. 2003. Aquaculture and Fisheries Biotechnology: Genetic
Approaches
Fredeen, H. 1986. Monitoring genetic changes. Aquaculture 57:1-26.
Hallerman, E. 2003. Population Genetics: Principles and Practices for Fisheries
Scientists. American Fisheries Society
Hardy, G. H. 1908. Mendelian proportions in a mixed population. Science
28:49-50.
Hartl, D. L., and A. G. Clark. 1997. Principles of Population Genetics. Sinauer
Associates, Massachusetts.
Lutz, C. G. 2001. Practical Genetics for Aquaculture. Iowa State University
Press, Iowa.
Purves, W. K. 1997. Life, the Science of Biology. Sinauer Associates, W.H.
Freeman
Raymond, M., and F. Rousset. 1995a. An exact test for population
differentiation. Evolution 41:823-833.
Raymond, M., and F. Rousset. 1995b. Genepop (ver 1.2): a population genetics
software for exact tests and ecumenicism. The Journal of Heredity
86:248-249.
Tave, D. 1993. Genetics for Fish Hatchery Managers. Van Nostrand Reinhold,
New York.
Weaver, R. F., and P. W. Hedrick. 1989. Genetics. Wn CBrown Publishers,
Iowa.
Weinberg, W. 1908. Uber Vererbungsgesetze beim Menschen. Z. Abst. V.
Vererb. 1:277-330.
36