Aula2

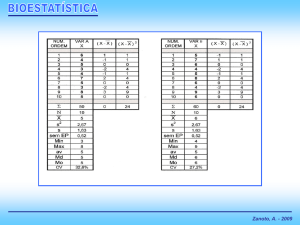
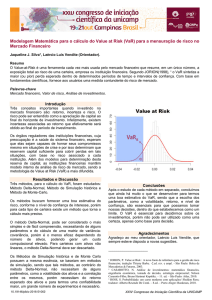
ORDEM
VAR 1
VAR 2
VAR 3
VAR 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
5
6
7
4
5
8
6
4
7
8
5
6
7
4
5
8
6
4
7
8
5
6
7
4
5
8
6
4
7
8
5
6
7
4
5
8
6
4
7
8
5
6
7
4
5
8
6
4
7
8
5
6
7
4
5
8
6
4
7
8
5
6
7
4
5
8
6
4
7
8
5
6
7
4
5
8
6
4
7
8
5
6
7
4
5
8
6
4
7
8
5
6
7
4
5
8
6
4
7
8
Zanoto, A. - 2009
SOMA
60
120
180
240
N
10
20
30
40
MÉDIA
6
6
6
6
D.P.
1,4907
1,4510
1,4384
1,4322
C.V.
24,85%
24,18%
23,97%
23,87%
Zanoto, A. - 2009
NUM.
DADOS
DADOS
DADOS
DADOS
ORDEM
VAR A
VAR B
VAR C
VAR D
1
3
3
4
8
2
4
4
0
0
3
3
2
7
0
4
2
4
3
7
5
4
5
1
0
6
3
3
6
6
7
5
4
0
0
8
4
2
5
6
9
3
3
2
8
10
4
5
7
0
S
35
35
35
35
X
3,5
3,5
3,5
3,5
s
0,85
1,08
2,72
3,75
CV
24,30%
30,90%
77,70%
107,10%
Zanoto, A. - 2009
Exemplo - Dados ou valores da variável, ordenados, em ordem crescente
ou ascendente:
22 25 28 32 35 43 46 51 55 83 83 98 99
Estatística descritiva:
Soma................................... S = 700,00
Frequência total.................. N = 13
Média aritmética.................. X = 53,85
Variância............................. s2 = 768,64
Desvio padrão..................... s = 27,72
Erro padrão....................... sem = 7,69
Mínimo................................ min = 22
Máximo.............................. max = 99
Amplitude de variação......... av = 77
Média geométrica................ G = 47,58
Média harmônica................. H = 42,18
Mediana.............................. Md = 46
Moda................................... Mo = 83
Frequência da moda........... fMo = 2
Coeficiente de Variação .. CV = 51,5%
Zanoto, A. - 2009
PROBABILIDADES
Probabilidade - É a medida de atitude de dúvida do espírito humano diante
de acontecimentos que podem ou não se realizar.
Probabilidade - Em um conjunto de eventos, é a possibilidade igual desses
eventos acontecerem.
A probabilidade constitui um axioma matemático, sem definição, assim como
o ponto e a reta em geometria.
Teoria das probabilidades - Início: 1654 - Blaise Pascal e Pierre Fermat
Questões apresentadas pelo jogador Barão A.G. Méré, sobre jogos de azar
(dados, lances de moedas, cartas de baralho, sorteios, etc.).
Continuação e aperfeiçoamento da teoria por Pascal, Fermat, Huygens,
Bernoulli, Kolmogorov, etc.
Terminologia relacionada: casualidade, fenômenos casuais, flutuações
casuais, acaso - “Acaso = Ignorância”.
“Matemática fractal” - (Mandelbrot) - “busca da lógica no aparentemente
ilógico da natureza”.
Zanoto, A. - 2009
Zanoto, A. - 2009
Inferência estatística - É o processo de generalizar para o universo ou
população correspondente, as conclusões obtidas a partir de uma amostra.
A inferência está montada em probabilidades.
Uma predição exata é pràticamente impossível, em consequência da
probabilidade de erro.
As probabilidades são representadas por índices de 0 a 1.
0% = 0/100 = 0 5% = 5/100 = 0,05 10% = 10/100 = 0,10
50% = 50/100 = 0,50 95% = 95/100 = 0,95 100% = 100/100 = 1,00
Distribuição binomial - É a distribuição de probabilidades apoiada em 2
eventos possíveis, mùtuamente exclusivos.
Ex: Moeda (cara ou coroa), Dado (par ou impar), Bola (branca ou preta), etc.
p = probabilidade de o evento acontecer: sucesso
q = probabilidade de o evento não acontecer: insucesso
q=(1-p)
se p = 0,5 então q = ( 1 - 0,5 ) = 0,5
Pr = Probabilidade ( P ) …….. P ou p
Zanoto, A. - 2009
Zanoto, A. - 2009
DISTRIBUIÇÃO AMOSTRAL DO NÚMERO DE CARAS
2 ^ 12 = 4096 AMOSTRAS
1000
900
800
FREQUÊNCIA
700
600
500
400
300
200
100
0
0
1
2
3
4
5
6
7
8
9
10
11
12
NÚMERO DE CARAS
Zanoto, A. - 2009
DISTRIBUIÇÃO AMOSTRAL
A distribuição amostral é uma distribuição teórica.
É a distribuição que obteríamos se pudéssemos tomar todas as
amostras possíveis, de mesmo tamanho, da mesma população,
extraindo cada uma aleatoriamente.
Teorema do limite central - Se uma variável tem distribuição com
média m e desvio padrão s e se extraímos amostras aleatórias de
tamanho N , então as médias dessas amostras, isto é, as X tem
distribuição aproximadamente normal, com média m e desvio
padrão s / N , para N suficientemente grande.
Zanoto, A. - 2009
Zanoto, A. - 2009
Zanoto, A. - 2009
CURVA DE DISTRIBUIÇÃO NORMAL
1733 - Descoberta por Abraham de Moivre
1812 - Redescoberta por Karl Friedrich Gauss e Pierre-Simon Laplace.
A curva de distribuição normal, ou curva de Gauss, tem a forma de sino e é a
representação gráfica da função matemática dada pela fórmula:
p =
e =
m =
s =
X =
f(X) =
constante numérica = 3,1416
base do logaritmo natural = 2,718
média aritmética da distribuição da população
desvio padrão da distribuição da população
variável aleatória representada no eixo abcissa
função de X no eixo ordenada
Zanoto, A. - 2009
Zanoto, A. - 2009
PROPRIEDADES DA DISTRIBUIÇÃO NORMAL
A área total sob a curva normal é igual à unidade, 1 , ou a 100%.
A área sob a curva, compreendida entre -1 e +1 desvios padrão é de 0,683
ou de 68,3% , portanto próxima de 2/3 da área total.
A área sob a curva, compreendida entre -1,96 e +1,96 desvios padrão é de
0,95 ou de 95% da área total.
A área sob a curva, compreendida entre -2,58 e +2,58 desvios padrão é de
0,99 ou de 99% da área total.
A curva normal é assintótica, isto é, as caudas da curva nunca chegam a
tocar o eixo da abcissa.
O campo de variação dos valores X da abcissa, vai teoricamente, de – a +
infinito.
Na curva normal, a mediana deve coincidir com a média aritmética.
Zanoto, A. - 2009
DISTRIBUIÇÃO NORMAL REDUZIDA OU PADRONIZADA
A distribuição normal depende de dois parâmetros: a média aritmética ( m ) e o desvio
padrão ( s ).
Existem tantas curvas normais quanto a variação combinada de m e de s .
A simplificação pode ser feita, convencionando-se que: m = 0 e s = 1.
Introduz-se agora uma nova medida ( z ) que significa quantos desvios padrão
um valor de ( x ) está afastado de ( m ).
z=
xm
s
Este valor será negativo, à esquerda de m e positivo, à direita de m.
Dessa forma a variável aleatória ( z ) terá distribuição normal com média aritmética igual a
0 e desvio padrão igual à unidade.
A equação da distribuição normal reduzida fica então:
z
1 
f ( x) =
e 2
2p
2
Zanoto, A. - 2009
Zanoto, A. - 2009
Zanoto, A. - 2009
Percentis - São medidas que dividem o conjunto ordenado de uma variável
em 100 partes iguais ( N / 100 ).
São medidas de posição na distribuição de uma variável.
Decis - São medidas porcentuais que dividem o conjunto ordenado dos
valores de uma variável em 10 partes iguais ( N / 10 ) : 10%, 20%, 30%, ....
Quartis - São medidas porcentuais que dividem o conjunto ordenado dos
valores em 4 partes iguais ( N / 4 ) : 25%, 50%, 75%, 100%.
O segundo quartil ( 50% ) corresponde à mediana.
Zanoto, A. - 2009
Zanoto, A. - 2009
Zanoto, A. - 2009
Zanoto, A. - 2009
Nome ______________________________________
Assinatura __________________________________
Data _______________________________________
Com os dados das duas Variáveis A e B, abaixo:
Variável A :
6 4 5 3 4 7 5 3 8 5
Variável B :
5 7 6 4 5 8 6 4 9 6
Calcular, com as respectivas abreviações estatísticas:
Soma, Freqüência total, Média aritmética, Variância, Desvio padrão,
Erro padrão, Mínimo, Máximo, Amplitude de variação, Mediana, Moda, e
Coeficiente de Variação.
Mostrar as etapas do cálculo da Variância.
Explicar qual das duas Variáveis é mais homogênea, estatisticamente.
Zanoto, A. - 2009