Aula4

INTERVALO DE CONFIANÇA DA MÉDIA DA POPULAÇÃO ( m )
O intervalo de confiança da média aritmética da população ( m ) pode ser
calculado a partir de:
X = média aritmética da amostra
s = desvio padrão da amostra
N = frequência total ou número de casos da amostra
a = nível de significância adotado
GL = graus de liberdade = ( N - 1 ) ou “degrees of freedom” = ( df )
t = valor de t na Tabela, de acordo com os graus de liberdade (GL) ou
(df)
1
( IC OU CI ) = X  t a
2
s
1
 m  X t a
2
N
s
N
Zanoto, A. - 2009
Zanoto, A. - 2009
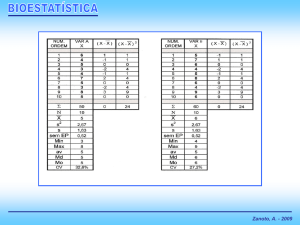
Exemplo:
X = 68,2
consequentemente:
s = 2,9
N = 10
a = 0,05
GL = df = (N-1) = (10-1) = 9
t = 2,262 na Tabela (para GL = df = 9)
2.9
2.9
68.2  2.262
 m  68.2  2.262
10
10
68.2 - 2.07 < m < 68.2 + 2.07
IC(95%) ou CI(95%) = 66.13 < m < 70.27
Zanoto, A. - 2009
Exemplo:
X = 1,5646
consequentemente:
s = 0,295
N = 65
a = 0,05
GL = df = (N-1) = (65-1) = 64
t = 2,000 (para GL = df = 60)
0.295
0.295
15646
.
 2.000
 m  15646
.
 2.000
65
65
1.5646 - 2.000 ( 0.295 / 8.06226) < m < 1.5646 + 2.000 (0.295 / 8.06226)
IC(95%) ou CI(95%) = 1.4915 < m < 1.6377
Zanoto, A. - 2009
PROVAS PARAMÉTRICAS
abcde-
Mensuração Quantitativa
Nível de mensuração – Escala numérica, intervalar ou de razão
Desvio Padrão e Coeficiente de Variação
Distribuição normal da amostra
N > 35
PROVAS NÃO PARAMÉTRICAS
OU
PROVAS DE ORDENAÇÃO
OU
PROVAS DE DISTRIBUIÇÃO LIVRE
abcdeef-
Mensuração Qualitativa
Nível de mensuração - Escalas categórica, nominal ou de classe e ordinal
Ordenação
Número pequeno de casos ou observações ( N < 20 )
Distribuição livre
Modelos mais específicos e mais recentes
Tabelas próprias
Zanoto, A. - 2009
Zanoto, A. - 2009
ESCOLHA DO MODELO ESTATÍSTICO
A escolha do modelo estatístico adequado vai depender principalmente de:
a- Nível de mensuração das variáveis:
CATEGÓRICA OU NOMINAL
QUALITATIVAS (NÃO-PARAMÉTRICO)
ORDINAL
INTERVALAR OU NUMÉRICA
QUANTITATIVAS (PARAMÉTRICO)
b- Número de variáveis: 1, 2, k (3 ou mais variáveis)
c- Tipos de variáveis: dependentes ou relacionadas e independentes
d- N (Frequência total de casos ou observações de cada variável)
Zanoto, A. - 2009
t não pareado - ( t de “Student” ) - “ unpaired t ”
Teste de igualdade das médias, para 2 amostras independentes.
“Student”: Gosset (estudioso)
Hipótese de Nulidade Ho: As médias aritméticas são iguais.
X1 = Média aritmética da amostra 1
X2 = Média aritmética da amostra 2
s1 = Desvio padrão da amostra 1
s2 = Desvio padrão da amostra 2
N1 = Número de casos da amostra 1
N2 = Número de casos da amostra 2
GL = Gráus de Liberdade =
= [ ( N1 + N2 ) - 2 ]
Teste bicaudal ( 2Q , na Tabela )
t
X1 X2
2
1
2
2
s
s

N1 N 2
Zanoto, A. - 2009
Zanoto, A. - 2009
Zanoto, A. - 2009
Zanoto, A. - 2009
t pareado - ( antes e depois ) - ( pré e pós )
Teste de igualdade para 2 amostras dependentes ou relacionadas
Hipótese de Nulidade: As amostras são iguais
D = Diferença entre os valores de cada par de dados
D = Média aritmética das diferenças de todos os pares de dados
sD = Desvio padrão das diferenças de todos os pares de dados
N = Número igual de casos =
= Número de pares de dados
GL = Gráus de Liberdade = ( N - 1 )
Teste monocaudal ( Q , na Tabela )
D
t
sD
N
Zanoto, A. - 2009
Zanoto, A. - 2009
Zanoto, A. - 2009