listadeexerciciomatematicabasicaI

CENTRO UNIVERSITÁRIO DO TRIÂNGULO
DISCIPLINA: MATEMÁTICA BÁSICA
PROFESSOR: CARLOS VENÍCIO SIQUEIRA
Lista de exercícios
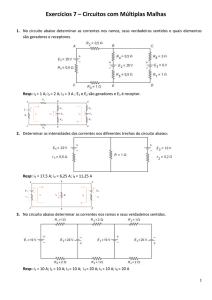
01) Considere a figura abaixo, onde um dos lados do trapézio retângulo se encontra apoiado sobre o
gráfico de uma função f. Sabendo-se que a área da região sombreada é 9cm2, a lei que define f é:
7x
2
a) y =
6
3x
1
b) y =
4
2x
1
c) y =
5
5x
1
d) y =
2
4x
1
e) y =
3
Resp.: e
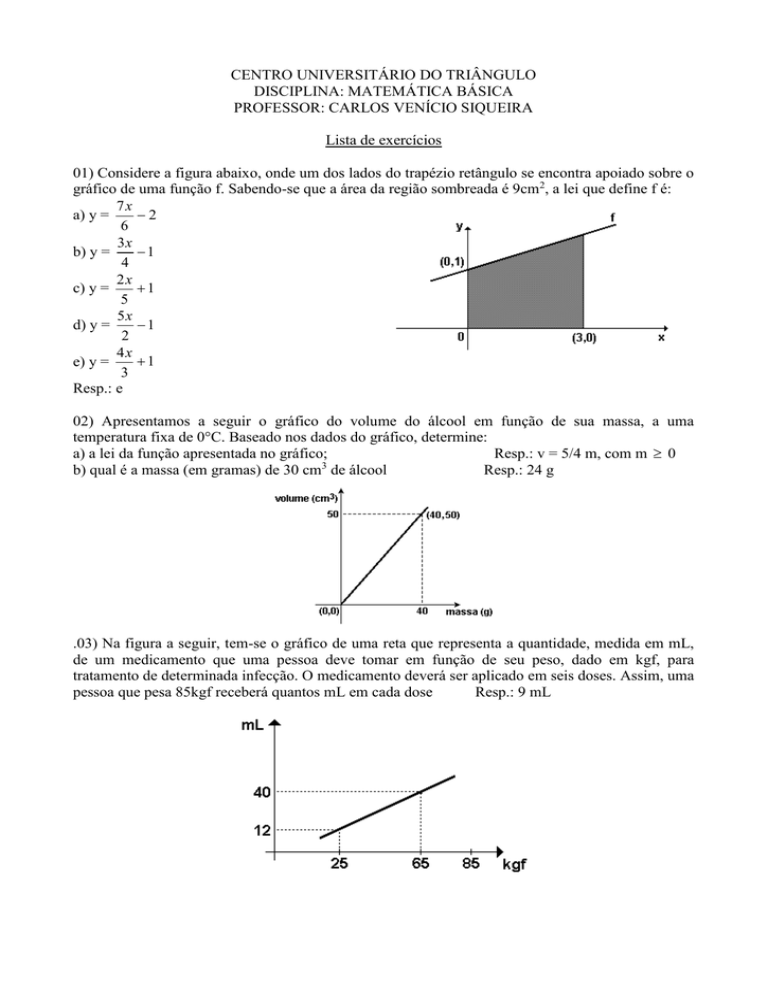
02) Apresentamos a seguir o gráfico do volume do álcool em função de sua massa, a uma
temperatura fixa de 0°C. Baseado nos dados do gráfico, determine:
a) a lei da função apresentada no gráfico;
Resp.: v = 5/4 m, com m  0
b) qual é a massa (em gramas) de 30 cm3 de álcool
Resp.: 24 g
.03) Na figura a seguir, tem-se o gráfico de uma reta que representa a quantidade, medida em mL,
de um medicamento que uma pessoa deve tomar em função de seu peso, dado em kgf, para
tratamento de determinada infecção. O medicamento deverá ser aplicado em seis doses. Assim, uma
pessoa que pesa 85kgf receberá quantos mL em cada dose
Resp.: 9 mL
04) A Cerâmica Marajó concede uma gratificação mensal a seus funcionários em função da
produtividade de cada um convertida em pontos; a relação entre a gratificação e o número de pontos
está representada no gráfico a seguir. Observando que, entre 30 e 90 pontos, a variação da
gratificação é proporcional à variação do número de pontos, determine a gratificação que um
funcionário receberá no mês em que obtiver 100 pontos.
05) A tabela mostra a expectativa de vida ao nascer de pessoas de um certo país: Supondo-se que a
expectativa de vida aumente de forma linear, pode-se afirmar que uma pessoa nascida nesse país, no
ano de 2010, deverá viver quanto tempo? Resp.: 77 anos, 7 meses e 9 dias.
Ano de nascimento
1960
1980 2000
Expectativa de vida (em anos)
66,6
71,0
75,4
Considere 1 ano como tendo 365 dias.
06) Um grande poluente produzido pela queima de combustíveis fósseis é o SO2 (dióxido de
enxofre). Uma pesquisa realizada na Noruega e publicada na revista "Science" em 1972 concluiu
que o número (N) de mortes por semana, causadas pela inalação de SO2, estava relacionado com a
concentração média (C), em mg/m3, do SO2 conforme o gráfico a seguir: os pontos (C, N) dessa
relação estão sobre o segmento de reta da figura. Com base nos dados apresentados, a relação entre
N e C (100  C  700) pode ser dada por? Resp.: N = 94 + 0,03 C
07) O custo C, em reais, para se produzir n unidades de determinado produto é dado por:
C = 2510 - 100n + n2.
Quantas unidades deverão ser produzidas para se obter o custo mínimo? Resp.: 50 unidades
08) A função real f, de variável real, dada por f(x)=-x2+12x+20, tem um valor
a) mínimo, igual a -16, para x = 6
b) mínimo, igual a 16, para x = -12
c) máximo, igual a 56, para x = 6
d) máximo, igual a 72, para x = 12
e) máximo, igual a 240, para x = 20
09) Observe a figura abaixo. Nessa figura, está representada a parábola de vértice V, gráfico da
x2
função de segundo grau cuja expressão é?
Resp.: y 
 2x
5
10) O gráfico da função y = ax2 + bx + c é a parábola da figura abaixo. Os valores de a, b e c são,
respectivamente? Resp.: - 1, 6 e 0
11) A figura abaixo representa o gráfico de uma parábola cujo vértice é o ponto V. A equação da
reta r é?
Resp.: y = 2x + 2
.
12) Supondo que no dia 5 de dezembro de 1995, o Serviço de Meteorologia do Estado de São Paulo
tenha informado que a temperatura na cidade de São Paulo atingiu o seu valor máximo às 14 horas,
e que nesse dia a temperatura f(t) em graus é uma função do tempo "t" medido em horas, dada por
f(t) = -t2 + bt - 156, quando 8 < t < 20.
Obtenha a temperatura máxima atingida no dia 5 de dezembro de 1995. Resp.: 40
13) A função f, de IR em IR, dada por f(x) = ax2 - 4x + a tem um valor máximo e admite duas raízes
reais e iguais. Nessas condições, f(-2) é igual a?
Resp.: - 2
14) Durante o processo de tratamento uma peça de metal sofre uma variação de temperatura
descrita pela função: f(t) = 2 + 4t – t2, 0 < t < 5. Em que instante t a temperatura atinge seu valor
máximo?
Resp.: 2
15) Um laboratório testou a ação de uma droga em uma amostra de 720 frangos. Constatou-se que a
lei de sobrevivência do lote de frangos era dada pela relação v(t) = at2 + b, onde v(t) é o número de
elementos vivos no tempo t (meses). Sabendo-se que o último frango morreu quando t = 12 meses
após o início da experiência, a quantidade de frangos que ainda estava viva no 10º mês é?
Resp.: 220