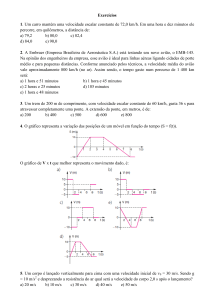
Exemplo 7. Encontre a velocidade instantânea da partícula descrita na Figura 1 nos
seguintes instantes: (a) t = 1.0 s, (b) t = 3.0 s, (c) t= 4.5 s, e (d) t= 7.5 s.
(a) t = 1.0 s
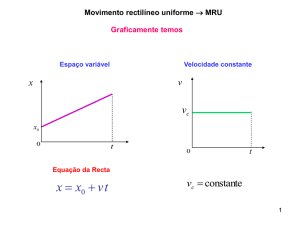
x x0 v t
Sabemos que entre 0 e 2 s a velocidade é
constante
x0 = 0
t0 = 0
x = 10 m
t=2s
v
x x0 10 m - 0
5.0 m/s
t
2s
Figura 1
(b) t = 3.0 s
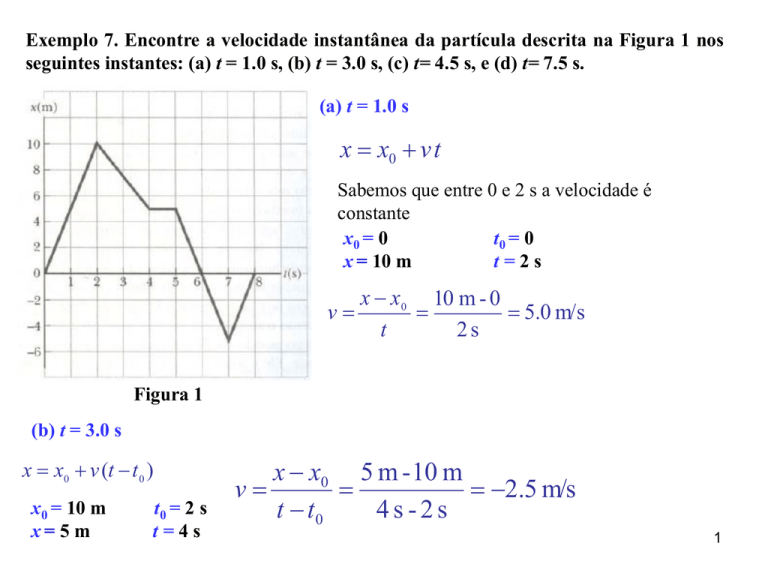
x x0 v (t t 0 )
x0 = 10 m
x= 5 m
t0 = 2 s
t=4s
x x0 5 m - 10 m
v
2.5 m/s
t t0
4s-2s
1
(c) t = 4.5 s
v= 0
(d) t = 7.5 s
x x0 v (t t 0 )
x0 = - 5 m
x =0m
t0 = 7s
t=8s
x x0 0 - (-5 m)
v
5 m/s
t t0
8s -7s
2
Aceleração média
Quando a velocidade da partícula se altera,
diz-se que a partícula está acelerada
A aceleração média é a variação da velocidade
am
v x num intervalo de tempo t
v f vi
t f ti
ou
v x
am
t
3
Exemplo 8. Considere o movimento do carro da Figura 2. Para os dados apresentados
na Figura 2, calcule a aceleração média do carro.
a
Figura 2
v f vi
A
velocidade
escalar
diminui com o tempo
15 m/s 30 m/s
am
7.5 m/s 2
t f ti
2.0 s 0
v
a
4
Aceleração instantânea
Em algumas situações a aceleração média pode variar em intervalos de tempo diferentes
portanto é útil definir a aceleração instantânea
v dv
a lim
t 0 t
dt
dv d dx d 2 x
a
2
dt dt dt dt
Aceleração na direcção x
a aex
ex
x
5
Movimento rectilíneo uniformemente variado
Um movimento é uniformemente variado quando a aceleração é constante
v v0 at
v0
é a velocidade da partícula
no instante t = 0
é a aceleração da partícula
é constante
se a velocidade da partícula aumenta com o tempo
o movimento é uniformemente acelerado
se a velocidade da partícula diminui com o tempo
o movimento é uniformemente retardado
Substituindo
dx
v
dt
Integrando fica
obtemos
dx
v0 at
dt
1 2
x x0 v0t at
2
6
Exemplo 9. Um avião parte do repouso e acelera em linha recta no chão antes de levantar
voo. Percorre 600 m em 12 s. a) Qual é a aceleração do avião? b) Qual é a velocidade do
avião ao fim de 12 s?
a) Qual é a aceleração do avião?
x0 0
1 2
x x0 v0t at
2
Substituindo os valores
1 2
x at
2
x0 0
v0 0
v0 0
(parte do repouso)
na equação
2 x 2 600 m 1200 m
2
8
.
3
m/s
a 2
t
144 s 2
12 s 2
b) Qual é a velocidade do avião ao fim de 12 s?
v0 0
v v0 at
(parte do repouso)
v at 8.3 m/s 2 12 s 100 m/s
7
Graficamente temos
Velocidade variável
Aceleração constante
x
a
v
Espaço variável
a
v0
x0
t
0
t
0
t
Parábola
Equação da recta
v v0 a t
0
a constante
1 2
x x0 v0t at
2
8
Corpos em queda livre
Galileo, o primeiro físico moderno, estudou a queda dos corpos
Refutou as hipóteses de Aristóteles
Através de experiências, mostrou que os corpos caem com a mesma
velocidade, independentemente de sua massa
9
Corpos em queda livre
Mas... devemos notar que em
geral, há outras forças actuando no
corpo considerado, o que pode
frustrar uma experiência se não
formos suficientemente cuidadosos
a
resistência
do ar!!
10
Corpos em queda livre
Vector aceleração da gravidade
g
O vector g aponta para baixo em
direcção ao centro da Terra
g
Valor da aceleração da gravidade
perto da superfície da Terra
g 9.8 m/s 2
As equações obtidas para partículas em movimento com aceleração constante são
aplicáveis ao corpo em queda livre. Assim
v v0 gt
1 2
y y0 v0t gt
2
y
g
ey
g ge y
11
y
Exemplo 10. Uma pedra é arremessada verticalmente para cima no
ponto A do terraço de um edifício com uma velocidade inicial de 20.0
m/s. O prédio tem 50.0 m de altura. Determine: a) o tempo no qual a
pedra atinge a sua altura máxima, b) a altura máxima acima do
terraço e c) o tempo no qual a pedra retorna ao nível do arremessador.
a) o tempo no qual a pedra atinge a sua altura máxima
Quando a pedra atinge a altura máxima ela pára e
v v0 gt
então v=0 no ponto máximo
Substituindo o valor de v na equação fica
0 v0 gt
v0 gt
v0 20.0 m/s
t
2.04 s
2
g 9.8 m/s
b) a altura máxima acima do terraço
y y0 v0t
1 2
gt
2
y0 0
t 2.04 s
Substituindo na equação fica
1
y (20 m/s)(2.04 s) (9.8 m/s 2 )( 2.04 s) 2 20.4 m
2
c) o tempo no qual a pedra retorna ao nível do arremessador
y y0 v0t
y0 0
1 2
gt
2
y0
t 0
1 2
1
0 v0t gt (v0 gt )t
2
2
t 4.08 s
1.2 Movimento em duas dimensões
Anteriormente estudamos uma partícula que se desloca em linha recta
Agora estudaremos o movimento de uma partícula no plano xy
A trajectória é o lugar geométrico dos pontos do espaço ocupados pelo corpo (planeta,
cometa, foguete, carro, etc.) que se movimenta
Qualquer ponto da trajectória pode ser descrito pelo vector posição. É definido em
termos de coordenadas cartesianas por
r xe x ye y
y
P
Trajectória s
ey
ex
r
A posição da partícula P na trajectória é descrita
pelo vector posição
r
x
13
Vector deslocamento
r
Quando uma partícula se desloca do ponto A para o ponto B no intervalo
de tempo
t t f t i
o vector posição passa de
ri
para
rf
y
ey
ex
A partícula se deslocou de
rf
B
r
A
ri
x
r r f ri
14
Velocidade média
r x y
vm
ex
ey
t t
t
vm vmxex vmy e y
ou
Velocidade instantânea
r dr dx dy
v lim
ex e y
t 0
t dt dt
dt
v v
ou
v v x ex v y e y
é a velocidade escalar
15
Aceleração média
v m
v x v y
am
ex
ey
t
t
t
ou
am amxex amy e y
Aceleração instantânea
dv y
dv
dvx
a
ex
e y
dt
dt
dt
ou
ou
2
dv
d r
a
dt
dt 2
a a x ex a y e y
a aceleração resulta de qualquer variação do vector velocidade
quer seja do módulo, da direcção ou do sentido de
v
16
MOVIMENTO DE UM PROJÉCTIL
A bola faz uma trajectória
curva
Para analisar este movimento consideraremos que
• a aceleração g é constante durante o intervalo do movimento e direccionada para
baixo
• o efeito da resistência do ar é desprezável
Com estas suposições a trajectória do projéctil é sempre uma parábola
17
Fotografia estroboscópica de bolas de ping-pong
A fotografia estroboscópica
regista
a
trajectória
de
objectos em movimento
A Figura mostra que a trajectória
da bola é uma parábola
18
v0
Analisamos o movimento
dimensões separadamente
em
cada
uma
das
Componentes da velocidade inicial
v0
ey
0
ex
v0 v0 x ex v0 y e y
v0 x
cos 0
v0
sin 0
As componentes iniciais
são
v0 x v0 cos 0
v0 y
v0
x e y da velocidade
v0 y v0 sin 0
19