ângulos - Educacional

ÂNGULOS
31/05/2017
REVISANDO
Ponto, Reta e Plano são noções primitivas dentre os conceitos geométricos.
Os conceitos geométricos são estabelecidos por meio de definições.
As noções primitivas são adotadas sem definição.
Como podemos imaginar ou formar idéias de ponto, reta e plano,
então serão aceitos sem definição.
Podemos ilustrar com as seguintes idéias para entender alguns
conceitos primitivos em Geometria:
Ponto: uma estrela, um pingo de caneta, um furo de agulha, ...
Reta: fio esticado, lados de um quadro, ...
Plano: o quadro negro, a superfície de uma mesa, ...
Notações de Ponto, Reta e Plano: As representações de objetos geométricos podem
ser realizadas por letras usadas em nosso cotidiano, da seguinte forma:
Pontos A, B, L e M representados por letras maiúsculas latinas;
Retas r, s, x, p, q, u e v representados por letras minúsculas latinas;
Planos Alfa, Beta e Gama representados por letras gregas minúsculas.
Plano Alfa (rosa), Plano Beta (azul claro) e Plano Gama (amarelo).
Observação: Por um único ponto passam infinitas retas.
De um ponto de vista prático, imagine o Pólo Norte
e todas as linhas meridianas (imaginárias) da Terra passando por este ponto.
Numa reta, bem como fora dela, há infinitos pontos,
mas dois pontos distintos determinam uma única reta.
Em um plano e também fora dele, há infinitos pontos.
Retas paralelas
Duas retas são paralelas se estão em um mesmo plano
e não possuem qualquer ponto em comum.
Se as retas são coincidentes ("a mesma reta") elas são paralelas.
Retas concorrentes
Duas retas são concorrentes se possuem um único ponto em comum.
Um exemplo de retas concorrentes pode ser obtido pelas linhas retas
que representam ruas no mapa de uma cidade e a concorrência ocorre
no cruzamento das retas (ruas).
Retas perpendiculares: são retas concorrentes que formam ângulos de 90 graus.
Usamos a notação a
b para indicar que as retas a e b são perpendiculares.
Semirretas: Um ponto O sobre uma reta s, divide esta reta em
duas semirretas.
O ponto O é a origem comum às duas semirretas que são
denominadas semirretas opostas.
Dada uma reta s e dois pontos distintos A e B sobre a reta,
o conjunto de todos os pontos localizados entre A e B,
inclusive os próprios A e B, recebe o nome de segmento de reta,
neste caso, denotado por AB.
O ÂNGULO E SEUS ELEMENTOS
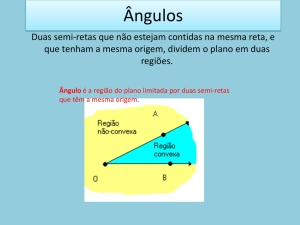
Duas semi-retas que não estejam contidas na
mesma reta, e que tenham a mesma origem,
dividem o plano em duas regiões: uma convexa e
outra não-convexa.
Cada uma dessas regiões, junto com as
semi-retas,forma um ângulo.
Assim, as duas semi-retas determinam dois ângulos:
Ângulo é a região do plano limitada por duas semi-retas
que têm a mesma origem.
Todo ângulo possui dois lados e um vértice.
Os lados são as semi-retas que determinam.
O vértice é a origem comum dessas semi-retas.
O ângulo também está associado à idéia de giro.
Observe as imagens abaixo e imagine de quantos
graus foi cada giro.
Podemos associar os ângulos às frações. Uma
volta completa representa 360º.
Desta forma temos:
Meia volta =
360 : 2 = 180
Um quarto de volta =
360 : 4 = 90
Um sexto de volta =
360 : 6 = 60
Para medir ângulos utilizamos um instrumento denominado transferidor.
O transferidor já vem graduado com divisões de 1º em 1º.
Existem dois tipos de transferidor: Transferidor de 180º e de 360º.
Todo ângulo cuja medida é menor que 90º denomina-se
ângulo agudo.
Todo ângulo cuja medida é maior que 90º e menor que
180º denomina-se ângulo obtuso.
Se a soma das medidas de dois ângulos é igual a 90º, então eles
são denominados ângulos complementares.
70º + 20º = 90º
70º
20º
Se a soma das medidas de dois ângulos é igual a 180º, então eles
são denominados ângulos suplementares.
50º + 130º = 180º
50º
130º
ÂNGULOS OPOSTOS PELO VÉRTICE (o.p.v.)
São congruentes.
São opostos pelo vértice
BISSETRIZ DE UM ÂNGULO
É a semirreta que divide o ângulo em dois ângulos
congruentes.
CONSTRUÇÃO DE ÂNGULOS COM TRANSFERIDOR E RÉGUA
20º
CONSTRUÇÃO DE ÂNGULOS COM TRANSFERIDOR E RÉGUA
20º
CONSTRUÇÃO DE ÂNGULOS COM TRANSFERIDOR E RÉGUA
125º
CONSTRUÇÃO DE ÂNGULOS COM TRANSFERIDOR E RÉGUA
125º
RIBEIRO
SIBELLE