Problemas NP-Completos - FACOM

Complexidade de Algoritmos
Aula 1
Introdução(1)


Existem algoritmos polinomiais para
todos os problemas? NÃO
Alguns problemas não podem ser
resolvidos, independente de quanto
tempo esteja disponível.

Problema da Parada (Halting Problem)


Dado um programa de computador com sua
respectiva entrada. Ele sempre pára?
Alguns problemas podem ser resolvidos,
mas não em tempo polinomial.
Introdução (2)


Problemas que podem ser resolvidos
em tempo polinomial são ditos
tratáveis.
Os que exigem tempo superpolinomial
são ditos intratáveis ou difíceis.
Introdução (3)


Problemas podem ser agrupados em
uma classe de problemas denominados
NP-completos.
Para os problemas nesta classe não foi
encontrado nenhum algoritmo de
tempo polinomial, nem foi provado que
não pode existir um algoritmo de tempo
polinomial.
Introdução (4)



Vários problemas NP-completos
parecem ser semelhantes a problemas
que têm algoritmos de tempo
polinomial.
Caminhos simples mais curtos x mais
longos.
Circuito de Euler x Circuito Hamiltoniano
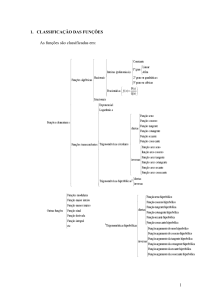
Classes P, NP, NP-completo


A classe P consiste nos problemas que podem
ser resolvidos em tempo polinomial.
A classe NP consiste nos problemas que são
verificáveis em tempo polinomial.



Para isto usamos um “certificado”, que é testado em
tempo polinomial.
Qualquer problema em P também está em NP.
Um problema está em NP-completo se ele está
em NP e é tão difícil quanto qualquer outro
problema em NP.
P=NP?
NP
P
NP-completo
Decisão x Otimização



Em um problema de otimização
queremos determinar uma solução
possível com o melhor valor.
Em um problema de decisão queremos
responder “sim” ou “não”.
Para cada problema de otimização
podemos encontrar um problema de
decisão equivalente a ele.
Como resolver problemas NPcompletos?




Algoritmos de Aproximação
Algoritmos Probabilísticos
Heurísticas
Algoritmos FPT