Introdução - ISR-UC - Universidade de Coimbra

Universidade de Coimbra
Departamento de Engenharia Electrotécnica e de Computadores
ELECTRÓNICA II (2004/2005)
Trabalho Prático Nº 4
Amplificadores Operacionais
1 - Introdução
O amplificador operacional (Amp. Op.) é um amplificador de acoplamento directo, de alto
ganho e destinado a ser utilizado com um circuito de realimentação. Pode realizar um grande
número de operações sobre sinais (daí o nome de operacional), e apresenta várias vantagens
em relação a circuitos discretos, nomeadamente o de ser de dimensões reduzidas (circuito
integrado monolítico), de baixo consumo de potência e de baixo preço.
O Amp. Op. é um circuito complexo e pode ter várias dezenas de transístores. Contudo, em
termos de constituição interna, reduz-se a 3 módulos principais: amplificador diferencial de
entrada seguido de um amplificador de alto ganho e finalmente de um amplificador de saída.
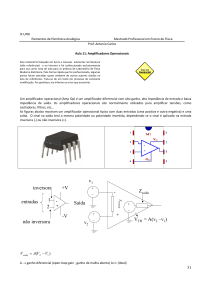
Na figura seguinte representam-se estes 3 módulos, embora de uma forma muito simplificada.
À saída do amplificador diferencial existe uma tensão que é proporcional à diferença das
entradas, vd = vi+vi. Esta diferença é amplificada (notar que o ganho é grande devido à fonte
de corrente no colector) e finalmente é aplicada a um amplificador de saída designado por
“push-pull”.
+VCC
vi+
v0
vi
VCC
Amp. Dif.
Amp.
Amp. saída.
figura 1
2- O Amplificador Operacional Ideal
O Amp. Op. tem duas entradas e uma saída, além dos terminais de alimentação, +VCC e
VCC. As entradas designam-se por entrada não inversora, (+) e entrada inversora, ().
1
À diferença entre as tensões de entrada chama-se entrada diferencial, vd = vi+vi. O ganho em
malha aberta do amplificador, Ad, que é a relação entre a tensão de saída e a tensão
diferencial, é muito elevado, tipicamente da ordem de 105 ou mesmo superior. A impedância
de entrada do Amp. Op. é muito elevada, da ordem das dezenas ou centenas de M, enquanto
a impedância de saída é baixa, da ordem das unidades ou dezenas de . Os Amp. Op. são
alimentados com fontes de alimentação, usualmente simétricas, +VCC e VCC.
Na figura 2 apresenta-se o símbolo do Amp. Op. e o modelo de um Amp. Op. que pode ser
utilizado para fazer uma análise funcional de circuitos com Amp. Op.s.
Na análise de circuitos lineares com Amp. Op.s é usual considerar estes como dispositivos
ideais a fim de simplificar a análise.
Um Amp. Op. ideal tem:
impedância de entrada infinita, impedância de saída nula e ganho em malha aberta infinito.
vi+
+
+
vd
vd
vo

vi
Ro
ii
+VCC
VCC


Ri
Ad v d
vo

figura 2a)
figura 2b)
3- Circuitos com amplificadores operacionais
Devido ao elevado ganho dos Amp. Op.s, estes são utilizados em circuitos com realimentação
negativa. Isto significa que a saída do Amp. Op. vai ser ligada por um circuito à sua entrada
inversora. Desta forma, a montagem torna-se estável no sentido que, se alguma perturbação
do circuito conduzir por exemplo a um aumento de vd, então a realimentação vai actuar de
forma a diminuir e estabilizar vd.
A noção de realimentação negativa ficará clara depois de se introduzirem 2 montagens típicas
com Amp. Op.s.
3.1 - Montagem não inversora
A montagem não-inversora representa-se na figura 3a). Para determinarmos o ganho da
montagem, considere-se a figura 3b) que utiliza o modelo do Amp. Op. da figura 2b).
As equações básicas são:
v0  Ad vd ; vi  vd  v f
R0=0
vi
vo
vd

vf
vo
vi
+
vd
Ri


Ad vd
R1
R2
R2
figura 3a)
R1
figura 3b)
2
Como a impedância de entrada é muito elevada (ou infinita), a tensão vf vem dada por
(divisor de tensão):
R2
vf 
v
R1  R2 0
Substituindo vf nas primeiras equações resulta:
v0
Ad
.

R2
vi
1  Ad
R1  R2
Finalmente, como Ad é um ganho muito elevado, chegamos à expressão do ganho da
montagem que é:
v0 R1  R2
R

 1 1
vi
R2
R2
Vejamos agora que a realimentação introduzida por R1 faz com que a montagem seja estável.
Se ganho Ad é muito elevado, então a tensão diferencial vd tem de ser muito próxima de zero.
Imagine-se que uma perturbação no circuito torna a tensão vd ligeiramente positiva. Desta
forma a tensão vo irá subir fazendo com que a tensão vf também suba. Mas com vi constante,
um aumento de vf faz com que a tensão vd baixe, anulando a perturbação.
Uma análise idêntica se poderia fazer considerando realimentação positiva, isto é, com as
estradas inversora e não inversora trocadas. Neste caso R1 seria ligado à entrada não-inversora
e a montagem seria instável: um aumento de vd conduz a uma diminuição de vo e também de
vf e, por sua vez, a um novo aumento de vd (em vez de uma diminuição). Em termos práticos
isto significa que a saída iria saturar, isto é, atingiria o mínimo (ou máximo) valor possível de
saída, próximo de VCC (ou de +VCC).
Notas:
i)- Esta montagem apresenta sempre um ganho superior ou igual a 1.
ii)- Com R2= e/ou R1=0, teremos uma montagem com ganho 1 conhecida como “seguidor
de tensão” (ver figura 5d)).
3.2 - Regras de análise de montagens com Amp. Op.s.
As montagens com Amp. Op. podem ser analisadas tendo em conta que estes são ideais, de
acordo com as duas regras seguintes (“regras de ouro”):
regra 1 : considerar as correntes de entrada num Amp. Op. nulas.
regra 2 : considerar vi+ = vi  (vd=0)
A primeira regra deriva de se considerar a impedância de entrada infinita e a segunda de se
considerar Ad um ganho infinito. Para analisar a montagem não inversora seria então apenas
necessário constatar que vi = vi (regra 2), logo a corrente em R2 (e em R1 pela regra 1) é i=
vi/R2 pelo que vo= i(R1+R2) resultando imediatamente a relação entre vo/vi pretendida.
3
3.3 - Montagem inversora
Vejamos agora a montagem inversora, nome que deriva de o ganho da montagem ser
negativo. A tensão na entrada não inversora é zero (regra 2), logo, a corrente em R2 e R1 é
i= vi/R2 e vo= iR1+0. Assim:
R1
vo
R
 1
vi
R2
R2

vi
vo
Nesta montagem chama-se à entrada não
inversora “ponto do massa virtual” pois trata-se
de um ponto de potencial zero apesar da
corrente não poder entrar no Amp. Op.
+
figura 4 - Montagem inversora
f
3.4 - Outras montagens com Amp. Op.s
Tendo em conta as regras referidas anteriormente, é fácil analisar outras montagens com
Amp. Op.s. Considere as montagens das figuras seguintes. Por exemplo, na figura 5a) a
tensão no terminal não inversor é 1/3 da soma das tensões de entrada; na figura 5c) a corrente
no condensador é i=Cdvi/dt, mas na figura 5e), i=vi/R. Utilizando as regras anteriores
determine a relação entre saída(s) e entrada e aperceba-se do significado do nome das
montagens.
R
v1
v2
R
R
+
vo
v3
R

R
R
v1
v2
C
R

R
2R

vi
vo
v3
vo
+
+
R
3
3
v o   vi
dvi
dt
i 1
figura 5b)- somador inversor figura 5c)- diferenciador
v o    vi
i 1
figura 5a)- somador não-inversor
v o   RC
C
vi
+
R
vo

vi

vo
+
v o  vi
figura 5d)- seguidor (buffer)
vo  
1
v dt
RC  i
figura 5e)-integrador
4
4- O Amplificador Operacional Real
O Amp. Op. real apresenta um conjunto de limitações, como seria de esperar. Entre elas as
mais importantes são as seguintes:
i) - saturação da tensão de saída. A tensão de saída não pode exceder, em módulo, as tensões
de alimentação, +VCC e -VCC. De facto os valores extremos são inferiores às tensões de
alimentação (1 a 2V) devido à existência dos transístores (e resistências) entre as tomadas das
tensões de alimentação e a saída, tal como se pode verificar pela figura 1. Notar que quando o
Amp. Op. satura, a tensão diferencial deixa de ser nula!
ii) - limitação da corrente de saída. O Amp. Op. tem internamente um limitador de corrente
de saída para evitar a sua destruição por sobreaquecimento.
iii) - Correntes de polarização. As correntes de entrada do Amp. Op. não podem ser nulas
pois são as correntes de base do amplificador diferencial. Contudo podem ser de facto muito
baixas, ou porque os transístores têm um ganho muito elevado, ou porque se utilizam FETs
nas entradas ou ainda devido à existência de técnicas especiais de redução destas correntes.
Estas correntes são tipicamente da ordem das décimas de A para muitos Amp. Op. Outro
factor a ter em conta é que estas correntes de polarização não são exactamente iguais; ao valor
médio da diferença dá-se o nome de correntes de “offset”.
iv) - tensão de “offset”. Esta limitação resulta da desigualdade entre as tensões VBE dos 2
transístores do amplificador diferencial. Quando a tensão diferencial, vd, for exactamente
nula, a tensão de saída poderá não o ser. A tensão de offset de entrada define-se como a
tensão diferencial que deverá existir nas entradas de forma a obter uma tensão de saída nula.
A tensão de offset é tipicamente de 1mV para os Amp. Op que iremos utilizar.
v) “slew-rate”. A taxa de variação do sinal à saída de um Amp. Op. é limitada. Ao seu valor
máximo, expresso em V/s, dá-se o nome de “slew-rate”. Por exemplo, para uma entrada
com forma de onda rectangular, a saída pode ser trapezoidal ou mesmo triangular devido ao
facto de o Amp. Op. não conseguir acompanhar uma variação de tensão tão abrupta. Para o
Amp. Op. que iremos utilizar este valor é próximo de 0,5V/s.
5
5 - Montagens
+10V
vi
R1=1K
+
vo

1K
R2
R2
+10V

vi
10V
10K
vo
+
R1=10K
-10V
figura 6a)
figura 6b)
a) Monte o circuito da figura 6a). Note que são necessárias duas fontes de alimentação e que
deve fazer chegar à placa de montagens pelo menos 3 fios.
b) Aplique agora ao circuito uma fonte de sinal sinusoidal ou triangular de 1kHz. Observe
simultaneamente as tensões de entrada e de saída e meça o ganho da montagem (com a
saída sem distorção).
c) Introduza uma componente contínua no sinal de entrada e verifique que também este valor
é amplificado (amplificação DC).
d) Coloque vi=0. Nesta situação, meça com um multímetro a tensão de saída, vo. Calcule a
R2
v .
tensão de offset de entrada, vio = vo/11, uma vez que v  
R1  R2 o
e) Aumente agora a amplitude do sinal vi até obter distorção na saída. Meça os valores
máximo e mínimo da saída. Nesta situação meça também a tensão diferencial de entrada e
verifique que esta diferença deixou de ser próxima de zero.
f) Aplique agora à entrada da montagem uma onda quadrada e observe em simultâneo saída e
entrada. Aumente a frequência do sinal de entrada até 100KHz. Meça o “slew-rate” do
Amp. Op.
g) Repita as alíneas a), b) e c) para o caso da montagem inversora da figura 6b).
h) Substitua a resistência R1 da montagem inversora por um condensador de 40 nF. Aplique
uma onda rectangular à entrada, e observe a saída. Justifique os resultados.
Offset Null
Inverting Input
Non-Inverting Input
VEE
1
2
3
4
8
741
7
6
5
NC - (not connected)
+VCC
Output
Offset Null
6