biologia - Sistema de Ensino Energia

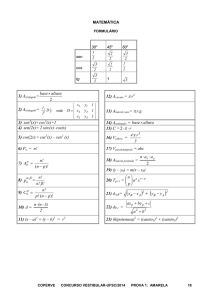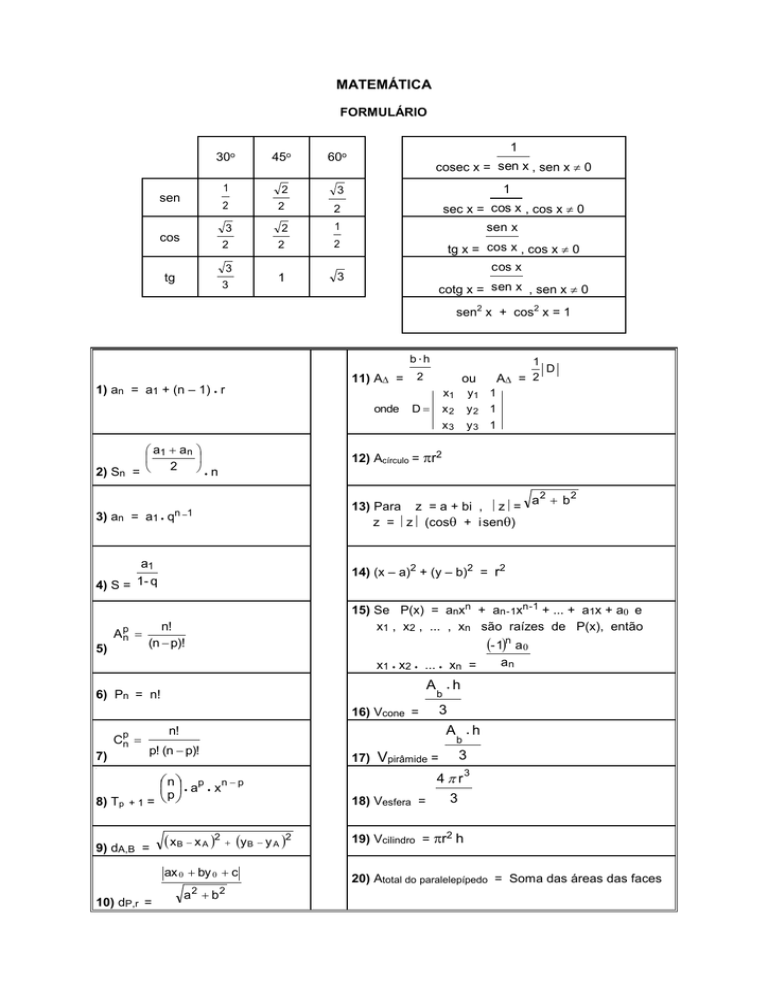
MATEMÁTICA
FORMULÁRIO
30o
45o
60o
1
2
3
sen
2
3
cos
2
3
tg
3
2
2
1
cosec x = sen x , sen x  0
1
sec x = cos x , cos x  0
2
1
2
2
1
3
sen x
tg x = cos x , cos x  0
cos x
cotg x = sen x , sen x  0
sen2 x + cos2 x = 1
b h
1) an = a1 + (n – 1)  r
11) A =
onde
2
1
D
2
A =
ou
D
x1
x2
y1 1
y2 1
x3
y3 1
 a1  a n 


2
n
2) Sn = 
12) Acírculo = r2
3) an = a1  qn –1
13) Para z = a + bi , z =
z = z  (cos + i sen)
a1
1
4) S = - q
14) (x – a)2 + (y – b)2 = r2
A pn 
5)
n!
(n  p)!
15) Se P(x) = anxn + an - 1xn - 1 + ... + a1x + a0 e
x1 , x2 , ... , xn são raízes de P(x), então
- 1n a 0
x1  x2  ...  xn =
A
6) Pn = n!

b
7)
p! (n  p)!
17)
 n   ap  xn  p
p
8) Tp + 1 =  
10) dP,r =

b
h
3
Vpirâmide =
[
9) dA,B =
h
A
n!
p
an
3
16) Vcone =
Cn 
a2  b2
4  r3
18) Vesfera =
3
 x B  x A 2  y B  y A 2
19) Vcilindro = r2 h
ax 0  by 0  c
20) Atotal do paralelepípedo = Soma das áreas das faces
a2  b2
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
25) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. Dizer que a multiplicação de dois números negativos tem por resultado um número positivo é uma afirmação
sem justificativa e que nada tem a ver com questões práticas.
02. O conjunto dos números racionais é suficiente para medir (com exatidão) todo e qualquer comprimento.
04. Seja x um número inteiro diferente de zero. A existência do inverso multiplicativo de x só é garantida no
conjunto dos números reais e no conjunto dos números complexos (já que R  c).
08. Os números como
nossa realidade.
2 e  (e outros irracionais) só estão relacionados a coisas abstratas e “distantes” da
16. Se no último aniversário de João, a soma de sua idade com a de seu pai e a de seu avô era 90 anos, e no dia
de seu nascimento esta soma era 75 anos, então João está com 5 anos.
Comentário
Resposta: 16
01. Incorreta. A afirmação (...) a multiplicação de dois números negativos tem por resultado um número positivo (...)
justifica-se, por exemplo, através do conceito de número simétrico. Para obtermos o simétrico de n, n  R,
multiplicamos n por (–1). Assim, vejamos alguns exemplos:
1) O simétrico de n = 7 é (–1) . 7 = –7
2) O simétrico de n = –8 é (–1) . (–8) = 8
O segundo exemplo confirma o fato de o produto de dois números negativos ser um número positivo.
02. Incorreta. Veja, por exemplo, que a diagonal de um quadrado de lado 1, cujo valor é 2 , não pode ser medida utilizandose apenas números racionais, já que 2 é irracional.
04. Incorreta. Se x é um inteiro não-nulo, o seu inverso multiplicativo já existe no conjunto dos números racionais (Q). É falso
dizer que só existe em R.
08. Incorreta. 2 é a medida da diagonal de um quadrado de lado 1;  é o quociente da divisão do comprimento de qualquer
circunferência pelo seu diâmetro.
16. Correta. No aniversário de João: J + P + A = 90  P + A = 90 – J (*)
No dia do nascimento de João:
(P – J) + (A – J) = 75
P + A – 2J = 75 (**)
Substituindo (*) em (**), temos: 90 – J – 2J = 75  15 = 3J  5 = J
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
26) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
 π
0, 
01. sen x  x para todo x   2  .
 π
0, 
02. sen x + cos x  1 para todo x   2  .
04. Para qualquer arco x pertencente à interseção dos domínios das funções trigonométricas vale a igualdade
2
cosec x
2
2
 sec x
cotg x
.
08. Os gráficos das funções f1(x) = sen x e f2(x) = 5sen x se interceptam numa infinidade de pontos.
16. Os gráficos das funções g1(x) = cos x e g2(x) = 3 + cos x não possuem ponto em comum.
32. Os gráficos das funções h1(x) = sen x e h2(x) = sen (x+1) se interceptam numa infinidade de pontos.
Comentário
Resposta: 63

x  0, 
 2 .
01. Correta. Representando y = sen x e y = x no plano cartesiano, temos sen x  x para
02. Correta.
sen x + cos x  1  (sen x + cos x)²  1²
sen² x + 2 . sen x . cos x + cos² x  1
2 sen x . cos x  0  sen (2x)  0

x  0, 
 2  , concluímos que:
Como a inequação acima é verdadeira para todo

sen x + cos x  1 para todo x  0,  é corr eta.
 2
04. Correta.
1
cossec² x
1
sen ² x
=
=
= sec² x
cos² x
cotg² x
cos² x
sen ² x
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
08. Correta. Construindo os gráficos, obtemos:
Os gráficos se interceptam em infinitos pontos nos quais o seno se anula.
16. Correta. Contruindo os gráficos, temos:
Os gráficos não se interceptam.
32. Correta. Contruindo os gráficos, obtemos:
Os gráficos se interceptam em infinitos pontos.
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
27) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. O conjunto solução da inequação log (x2  9)  log (3  x) é
S = (, 4]  [3, +).
02. Para todo x real diferente de zero vale ln |x| < ex.
04. log 360 = 3  log 2 + 2  log 3 + log 5.
08. Considere as funções f(x) = ax e g(x) = logax.
Para a > 1, temos f crescente e g decrescente e para 0 < a < 1, temos f decrescente e g crescente.
16. A equação
ex  ex
2
não possui solução inteira.
32. Se log N =  3,412 então log
N =  6,824.
Comentário
Resposta: 04
01. Incorreta.
log (x²  9)  log (3  x)
x²  9  3  x
x² + x  12  0
x1 =  4
x2 = 3
Condição de existência
x² – 9 > 0
e
x1 =  3
x2 = 3
3–x>0
–x > –3
x<3
A solução da inequação será a intersecção dos intervalos:
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
02. Incorreta. Para x = –e, tem-se:
In | x| < e x
In |  e| < e e
1
In e < e
Obs.: e = 2,7...
e
1
1< e
e
1
e
Está incorreta pois e está entre 0 e 1.
04. Correta.
log 360 = log (2³ . 3² . 5)
log 360 = log 2³ + log 3² + log 5
log 360 = 3 . log 2 + 2 . log 3 + log 5
08. Incorreta. Para a > 1, as duas funções são crescentes e, para 0 < a < 1, as duas funções são decrescentes.
16. Incorreta.
ex = ex
2
x = x2
x²  x = 0
x1 = 0 ou x 2 = 1  S = {0, 1}
As duas soluções são inteiras.
32. Incorreta.
log
N = log (N)
log
N =
log
1
2
=
1
. log N
2
1
. (  3, 412)
2
N =  1,706
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
28) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. O valor numérico do polinômio p(x) = x2  4x + 5 para x = i é p(i) = 4  4i.
2i
02. O conjugado do número complexo z =
1
04. O determinante
1
i
é 1 + 2i.
1
1
1 1
1 i 1 i 0
define um número complexo. O módulo desse número complexo é 1 (um).

08. A forma trigonométrica do número complexo z = 1  i 3 é z = 
2 cos
5π
3
 isen
5π 

3 .
f (2  i )
16. Dadas as funções f(x) = x2  2x + 1 e g(x) = x2 + x, o valor do quociente
g (1  i )
3
i
é  5 + 5.
Comentário
Resposta: 27
01.
Correta.
P(x) = x² – 4x + 5  x = i
P(i) = i² – 4i + 5 = –1 – 4i + 5 = 4 – 4i
02. Correta.
2 + i (i)
2i  i²
2i + 1
Z=
.
=
=
= 1  2i
i
(i)
i²
1
Z = 1 + 2i
04. Incorreta.
1
1
1+ i
1
1
1  i
1
1 = 0  Z = 0  | Z| = 0
0
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
08. Correta.
Z= 1 
3i
–
² = 1² +
3
2
= 2
sen x =
3
2

x = 60°
5
3
5

5 
Z = 2  cos
+ i . sen

3
3 

 = 300° =
16. Correta.
f(x) = x² – 2x + 1
g(x) = x² + x
f(2 + i)
(2 + i)² – 2.(2 + i) + 1
4 + 4i + i²
=
=
g(1  i)
(1  i)² + (1  i)
1  2i +
2i
(1 + 3i)
2i + 6i²
6 + 2i
3
.
=
=
=
+
1  3i (1 + 3i)
1  9i²
10
5
 4  2i + 1
=
i² + 1  i
i
5
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
29) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. Uma P.A. e uma P.G., ambas crescentes, têm o primeiro e o terceiro termos respectivamente iguais.
Sabendo que o segundo termo da P.A. é 5 e o segundo termo da P.G. é 4, a soma dos 10 primeiros
termos da P.A. é 155.
02. Uma empresa, que teve no mês de novembro de 2002 uma receita de 300 mil reais e uma despesa de 350 mil
6
reais, tem perspectiva de aumentar mensalmente sua receita segundo uma P.G. de razão 5 e prevê que a
despesa mensal crescerá segundo uma P.A. de razão igual a 55 mil. Neste caso, o primeiro mês em que a
receita será maior do que a despesa é fevereiro de 2003.
04. Suponha que um jovem ao completar 16 anos pesava 60kg e ao completar 17 anos pesava 64kg. Se o
1
aumento anual de sua massa, a partir dos 16 anos, se der segundo uma progressão geométrica de razão 2 ,
então ele nunca atingirá 68kg.
08. Se os raios de uma seqüência de círculos formam uma P.G. de razão q , então suas áreas também
formam uma P.G. de razão q.
Comentário
Resposta: 07
01.
Correta.
(x, 5, y) P.A.  5 – x = y – 5  x + y = 10  y = 10 – x
y
4
(x, 4, y) P.G. 
=
 xy = 16
x
4
x(10  x) = 16
10 x  x² = 16
 x² + 10x  16 = 0
x²  10x + 16 = 0
x' = 2
x" = 8
x=2  y=8
x=8  y=2
Como a P.A. é crescente  (2, 5, 8)
(a1 + a n )n
(a1 + a10 )10
 S10 =
= (a1 + a10 ) . 5
2
2
= a1  9R  2  9.3  2  27  29
Sn =
a10
S10 = (a1 + a10 ) . 5 =
S10 = (2 + 29) . 5 =
S10 = 31 . 5 = 155
02. Correta.
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
Receita:
CONCURSO VESTIBULAR-UFSC/2003
P.G.  nov. 300  dez: 300 .
PROVA 1 - AZUL
6
6
6
= 360  jan: 360 .
= 432  fev: 432 .
= 518,4
5
5
5
Despesa:
P.A.  nov. 350  dez: 350 + 55 = 405  jan : 405 + 55 = 460  fev: 460 + 55 = 515
Então, em fev.: receita = 518.400,00
despesa = 515.000,00
Logo, receita > despesa.
04. Correta.
(60, 64, 66, 67, ...)
1
(4, 2, 1, ...) P.G.: q = 2
a1
4
4
S=
=
=
= 8
1
1
1  q
1 
2
2
60 + 8 = 68, mas isso só ocorrerá se o jovem viver infinitamente, pois a soma é ilimitada.
08. Incorreta.
(R1 , R 2 , R 3 , ...) q1 =
a2
R
R
= 2  q1 = 2
a1
R1
R1
Áreas
2
(R 21 , R 22 , R 2 3 , ...) q 2 =
a2
R 22
R 22
R 
=
=
=  2  = q 12
2
a1
R12
R1
 R1 
então: q 2  q1
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
30) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. Se uma loja vende um artigo à vista por R$ 54,00, ou por R$ 20,00 de entrada e mais 2 pagamentos mensais
de R$ 20,00, então a loja está cobrando mais do que 10% ao mês sobre o saldo que tem a receber.
02. Se o produto P é vendido por R$ 20,00 pela loja A e por R$ 40,00 pela loja B, então pode-se dizer que na loja
B o produto P está com o preço 100% acima do preço praticado pela loja A, e que a loja A está praticando um
preço 100% menor do que o praticado pela loja B.
04. Se numa área urbana o número de pessoas atingidas por certa doença (não controlada) aumenta 50% a cada
t
3
 
mês, então a função n(t) = N  2  fornece o número (aproximado) de pessoas afetadas pela doença, t

meses após o instante em que havia N pessoas doentes nessa área.
08. Admita que a função n(t) = N 2t forneça o número aproximado de pessoas atingidas por uma epidemia (não
controlada) onde t é o número de meses decorridos a partir do momento em que N pessoas são
acometidas pela doença. Então é correto afirmar que, num aglomerado urbano com 10.000 habitantes, não
ocorrendo aumento populacional, 8 meses após existirem 50 pessoas doentes é provável que toda a
população estará doente, caso nada seja feito para debelar o mal.

Comentário
Resposta: 13
01. Correta. Supondo uma taxa de 10% ao mês, verificamos que o saldo devedor é de R$54,00 – R$20,00 = R$34,00.
Após um mês, temos: R$34,00 + 10% de R$34,00 = R$37,40. O novo saldo devedor será de R$37,40 – R$20,00 =
R$17,40.
Após mais um mês: R$17,40 + 10% de R$17,40 = R$19,14.
Como a última prestação é de R$20,00, ou seja, maior que R$19,14, então a taxa do mês deve ser superior a 10%.
02. Incorreta. É correto dizer que o aumento de R$20,00 para R$40,00 é de 100%, mas é incorreto afirmar que a redução de
R$40,00 para R$20,00 é de 100%, pois é de 50%.
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
04. Correta.
08. Correta.
Do texto, temos: N = 50
Para t = 8: n(t) = N . 2t
n(8) = 50 . 28
n(8) = 50 . 256
n(8) = 12.800 pessoas
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
31) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. A solução da equação (x + 3)! + (x + 2)! = 8 (x + 1)! é 0 (zero).

02. A solução da equação Ax, 3 = 4 Ax, 2 é 6.

04. Um time de futebol de salão é formado por 5 jogadores. Dispondo de 8 jogadores, podemos formar 64 times
de futebol de salão.
08. O número de anagramas que podemos formar com as letras da palavra BRASIL, que começam com B e
terminam com L, é 24.
16. No desenvolvimento do binômio 2x  1 , o termo independente de x é 1.
6
Comentário
Resposta: 27
01. Correta.
(x + 3)! + (x + 2)! = 8 . (x + 1)!
x² + 5x + 6 + x + 2 = 8  x² + 6x = 0
x=0
ou
x = –6
verdadeira
falsa
02. Correta.
Ax, 3 = 4 . Ax, 2 



1
1
x!
x!
= 4.
(x  3)!
(x  2)!
(x – 2)! = 4 . (x – 3)! 
(x – 2) . (x – 3)! = 4 . (x – 3)!
x–2=4 x=6
04. Incorreta.
C8,5 =
8!
8.7.6
=
= 56 times
5! 3!
3.2.1
08. Correta.
16. Correta.
(2x – 1)6 possui como termo independente o sétimo termo:
6 
T7 =   . (2x)0 . (  1)6  T 7 = 1
6 
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
32) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. O número de elementos de uma matriz quadrada de ordem 12 é 48.
02. Somente podemos multiplicar matrizes de mesma ordem.
04. Uma matriz quadrada pode ter diversas matrizes inversas.
x x x
08. A soma das raízes da equação
4
4
x x
4 x
= 0 é 8.
3x  2y  0

xy 0
16. O sistema 
é indeterminado.
Comentário
Resposta: 08
01. Incorreta.
Se A é quadrada de ordem 12, então ela terá (12 x 12 = 144) elementos.
02. Incorreta.
O produto de duas matrizes, A e B, será possível quando o número de colunas de A for igual ao número de linhas de B.
04. Incorreta.
A matriz quadrada pode não ter inversa (det A = 0) e, se possuir inversa, ela será única.
08. Correta.
x³ + 4x² + 16x – 4x² – 4x² – 4x² = 0
x³ – 8x² + 16x = 0
x(x² – 8x + 16) = 0
x = 0 ou
4
x²  8x + 16 = 0
4
0+4+4=8
16. Incorreta.
 3x – 2y = 0

 x+ y= 0
=
3
–2
1
1
= 3  2= 5 0
Como  0, o sistema homogêneo é determinado.
33) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
01. Para que o polinômio p(x) = (a + b) x2 + (a  b + c) x + (b + 2c  6) seja identicamente nulo, o valor de c é
4.
02. O resto da divisão do polinômio x6  x4 + x2 por x + 2 é 52.
04. Dado o polinômio p(x) = x4 + 8x3 + 23x2 + 28x + 12 é correto afirmar que 2 é raiz de multiplicidade 3 para
p(x).
08. A equação polinomial x3  2x2  4x + 1 = 0 possui as raízes a, b e c. Logo, a soma a2 + b2 + c2 é igual a 12.
Comentário
Resposta: 10
01. Incorreta.
Condições:
= 0
a + b

a  b + c = 0
 b + 2c = 6

Resolvendo o sistema, temos:
a = 65 b = 65
c = 12 5
02. Correta.
P(x) = x6 – x4 + x²
D(x) = x + 2
R = P(–2)
R = (–2)6 – (–2)4 + (–2)²
R = 52
04. Incorreta.
Usando Briot-Ruffini sucessivas vezes, concluímos que x = –2 possui multiplicidade 2.
08. Correta.
x³ – 2x2 – 4x + 1 = 0, por Girard, verificamos que:
a + b + c = 2 (I )

ab + ac + bc =  4 (I I )
I) (a + b + c)² = 2²  a² + b² + c² + 2 . (ab + ac + bc) = 4
a² + b² + c² = 4 – 2 . (–4)
a² + b² + c² = 12
34) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. Os catetos de um triângulo retângulo medem 30cm e 50cm. Pelo ponto do menor cateto, que dista 6cm do
vértice do ângulo reto, traça-se uma reta paralela à hipotenusa. O menor dos segmentos determinados por
essa reta no outro cateto mede 10cm.
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
02. Dois triângulos são semelhantes quando têm os lados correspondentes proporcionais.
04. Num triângulo isósceles com 24cm de altura e 36cm de base, cada um dos lados iguais mede 60cm.
08. Uma rampa plana com 10m de comprimento faz um ângulo de 15 o com o plano horizontal. Uma
pessoa que sobe inteiramente a rampa eleva-se verticalmente 9,66m.
Dados: sen 15o = 0,259; cos 15o = 0,966 e tg 15o = 0,268.
Comentário
Resposta: 03
01. Correta.
Usando Tales,
6
x
=
 x = 10 cm
24
50  x
02. Correta. Trata-se da definição de triângulos semelhantes.
04. Incorreta.
No triângulo ABC, temos:
x² = 24² + 18²
x = 30 cm
08. Incorreta.
Queremos calcular h:
h
10
h
0,259 =
10
h = 2,59 m
sen 15° =
35) Em uma pirâmide quadrangular regular a aresta lateral mede 5cm e a altura mede 4cm. O volume, em cm 3, é:
Assinale no cartão-resposta o resultado numérico encontrado.
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
Comentário
Resposta: 24
No triângulo VAH, observamos que:
x² + 4² = 5²  x = 3 cm
A base da pirâmide é um quadrado de diagonal 6 cm:
a² + a² = 6²
a² = 18  a = 3 2 cm
Assim, o volume é:
1
V=
. 3 2
3


2
. 4  V = 24 cm³
36) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. x2 + y2  2x + 6y + 1 = 0 é a equação da circunferência de raio r = 3 que é concêntrica com a circunferência
x2 + y2 + 2x  6y + 9 = 0.
1
02. O coeficiente angular da reta que passa pelos pontos A(3, 2) e B(3, 1) é 2 .
04. Sabe-se que o ponto P(p, 2) é eqüidistante dos pontos A(3, 1) e B(2, 4). A abscissa do ponto P é 1.
08. As retas r: 2x  3y + 5 = 0 e s: 4x  6y  1 = 0 são perpendiculares.
16. O ponto P(3, 4) é um ponto da circunferência de equação x2 + y2  x + 4y  3 = 0.
Comentário
Resposta: 06
01. Incorreta.
: x² + y² – 2x + 6y + 1 = 0  centro (1, –3)
: x² + y² + 2x – 6y + 9 = 0  centro (–1, 3)
C1  C2  não são concêntricas
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS
COPERVE/UFSC
CONCURSO VESTIBULAR-UFSC/2003
PROVA 1 - AZUL
02. Correta.
3 3 x 3
= 0
2 1 y 2
–
–3 – 3y + 2x + 6 + x – 3y = 0
3x – 6y + 3 = 0 (÷3)
x – 2y + 1 = 0
2y = x + 1
D= 0 
04. Correta.
d PA = d PB  equidistante
(p – 3)² + (2 – 1)² = (p – 2)² + (2 – 4)²
p ²  6p + 9 + 1 = p ²  4p + 4 + 4
2p =  2  p = 1
08. Incorreta.
r: 2x  3y + 5 = 0  3y = 2x + 5 
s: 4x  6y  1 = 0  6y = 4x  1 
2
3
2
ms =
3
mr =
m r = m s  são paralelas
16. Incorreta.
P(3, 4)  x² + y²  x + 4y  3 = 0
3² + 4²  3 + 4 . 4  3 = 0
9 + 16  3 + 16  3 = 0
LEMBRE-SE DE MARCAR NO CARTÃO-RESPOSTA A
PROPOSIÇÕES QUE VOCÊ CONSIDERAR VERDADEIRAS.
SOMA DOS NÚMEROS
ASSOCIADOS ÀS