Sistemas Trifásicos

ANÁLISE DE CIRCUITOS EM
CORRENTE ALTERNADA
Sistemas Trifásicos
Em geral, em um sistema polifásico existem duas
ou mais tensões de mesma frequência mas com
fases diferentes, o sistema polifásico é simétrico
se as tensões são iguais e defasadas entre si por
um ângulo 2/n, onde n é o número de fases.
Se cada tensão ou fase atuar independentemente
das outras, dizemos que o sistema é não
interligado. A grande desvantagem do sistema é
que usa um número muito grande de fios (2n),
p.ex. num sistema trifásico usam-se seis fios.
Num sistema polifásico interligado, as fases
individuais são interligadas eletricamente.
Sistemas Trifásicos
Em relação a um sistema monofásico, o sistema
polifásico apresenta algumas vantagens:
a) A mesma potência elétrica pode ser
transmitida usando fios de bitola menor. É
claro que a vantagem só aparece quando a
potência for alta.
b) Com um sistema polifásico pode ser
produzido um campo magnético girante,
usado no acionamento de máquinas síncronas.
Sistemas Trifásicos
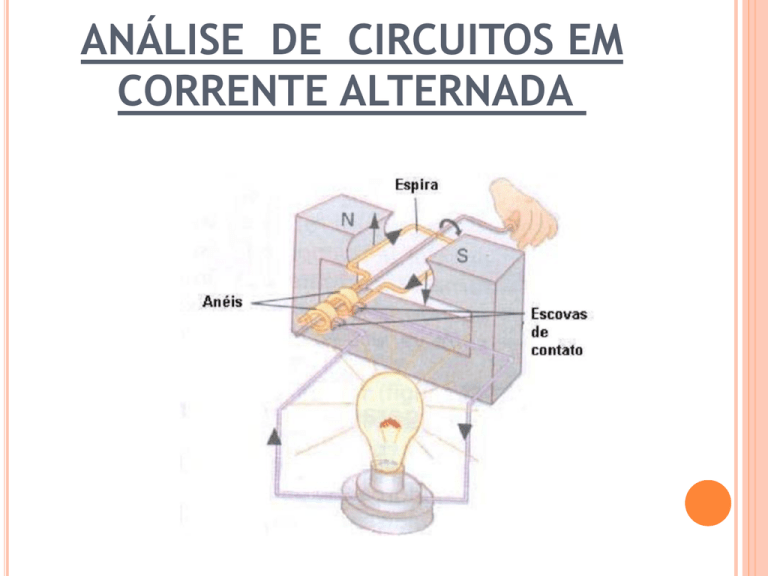
O gerador monofásico de corrente
alternada é uma aplicação da indução
eletromagnética,
convertendo
energia
mecânica
em
energia
elétrica. A espira (enrolamento na
prática) girando em um campo
magnético sob a ação de uma força
externa (turbina, motor a diesel,
etc) faz aparecer uma tensão
induzida nos terminais da espira, que
está ligada a anéis coletores.
Através das escovas é feito a
ligação entre o circuito externo e a
espira.
Sistemas Trifásicos
O circuito externo (carga) é conectado à espira
(ou enrolamento) através de anéis coletores e
escovas.
Sistemas Trifásicos
A f.e.m obtida nos terminais da espira é dada por:
e = VM.sen  = VM.sen t
Onde VM (tensão de pico) é proporcional a B
(campo magnético), l (comprimento do condutor e
vt (velocidade tangencial do condutor)
e = .l.vt
e = .l.v.sen 
e = VM.sen  = VM.sen t
Sistemas Trifásicos
Para gerar a mesma f.e.m., ao invés da espira girar
num campo magnético estacionário, pode-se, ter
um campo girante e a espira fixa, o efeito é o
mesmo.
Sistemas Trifásicos
Em
um
gerador
trifásico
existem
três
enrolamentos separados fisicamente de 120º entre si. Em
cada um dos enrolamentos será induzida uma tensão que
tem o mesmo valor, mas defasadas entre si de 120º.
Estrutura de um gerador trifásico ( três
enrolamentos - BY - AX -CZ )
SISTEMAS TRIFÁSICOS
As três tensões (V1, V2, V3) induzidas nos três enrolamentos (I, II, III)
Os três enrolamentos são estáticos e têm o mesmo número
de espiras. Esta parte do enrolamento é denominada
estator. Os pontos A,B e C representam uma das
extremidades e os pontos X Y e Z a outra extremidade.
SISTEMAS TRIFÁSICOS
SISTEMAS TRIFÁSICOS
As tensões de linha dão definidas pelas equações:
SISTEMAS TRIFÁSICOS
Diagramas fasoriais: tensões de fase e de linha
SISTEMAS TRIFÁSICOS
Se cada fase do gerador é conectada a circuitos separados,
teremos um sistema trifásico não interligado, o qual
necessita de seis fios para as ligações com a carga
trifásica.
Este sistema não é econômico, na prática os métodos de se
interligar as fases são: a ligação estrela (Y) e a ligação em
triângulo (∆) .
SISTEMAS TRIFÁSICOS
Ligações das cargas
As cargas trifásicas industriais (ex.: motores
elétricos)
são
equilibradas.
As
cargas
monofásicas e bifásicas (ex.: iluminação, aparelhos
eletrodomésticos, motores monofásicos, etc.)
devem ser eqüitativamente distribuídas entre as
fases de modo que o sistema não fique
desequilibrado.
SISTEMAS TRIFÁSICOS
Ligações das cargas
Dado um sistema de distribuição de baixa tensão (rede
secundária) a partir de um sistema de potência.
Diagrama unifilar de um sistema de potência
SISTEMAS TRIFÁSICOS
Ligações das cargas
Sistema de distribuição
SISTEMAS TRIFÁSICOS
Ligações das cargas: Observando a rede secundária podemos
notar que algumas cargas são alimentadas por tensão de fase e
outras por tensão de linha. Assim sendo, no cômputo geral das
cargas, podemos distinguir dois tipos de ligações: estrela e triângulo.
SISTEMAS TRIFÁSICOS
Ligações das cargas:
Sistemas Trifásicos – Ligação Estrela
Numa ligação estrela os pontos X, Y e Z são interligados
entre si, formando um ponto comum chamado de neutro (N).
O sistema assim obtido tem 4 fios de ligação
Sistemas Trifásicos – Ligação Estrela
Sistemas Trifásicos
– Ligação Estrela
Carga Balanceada
A carga é dita balanceada quando as impedâncias de cada fase
forem iguais em módulo e fase e IN=0. Neste caso, as
defasagens entre tensão e corrente são iguais A= B=C= 
Sistemas Trifásicos
Considerando Za = Zb = Zc =
fase são dadas pelas expressões:
– Ligação Estrela
, (carga equilibrada) as correntes de
Sistemas Trifásicos
Diagrama fasorial
– Ligação Estrela
Sistemas Trifásicos
– Ligação Estrela
Exercício: no circuito abaixo considere que as tensões de
fase valem 120V (eficazes) e que a carga é resistiva e
equilibrada , valendo 10 Ω. Calcule: a) Tensão de linha (VL) b)
Corrente de fase c) Corrente de linha d) Corrente no neutro
Sistemas Trifásicos
Resolução:
a) A tensão de linha será
b) IF=IL =120/10 =12 A, como a carga é resistiva as
correntes em cada fase estarão em fase com as
respectivas tensões. P.ex. se VA=120V0º VB=120V120º e VC=120V120º.
c) Logo: IA= (120V0º) /10 = 12A 0º =12A
IB= (120V -120º) /10 = 12A -120º = -6-j10,39 (A)
IC= (120V 120º) /10 = 12A 120º = -6+j10,39 (A)
d) A corrente no neutro é a soma das três correntes acima IN =
12 +(-6-j10,39) +-6+j10,39 = 0
Sistemas Trifásicos
Carga Desbalanceada
A carga é dita desbalanceada quando as
impedâncias de cada fase possuírem módulos ou
fases diferentes e IN≠ 0. Neste caso, as
defasagens entre tensão e corrente em cada fase
são também diferentes A≠ B≠C.
Sistemas Trifásicos
Carga Desbalanceada
Caso não haja o fio de retorno (neutro), as
tensões nas cargas são diferentes das tensões de
fase.
Sistemas Trifásicos
Sistemas Trifásicos
Exercício: no circuito abaixo considere que as tensões de
fase valem 120V (eficazes) e que a carga é resistiva e sendo
seus valores, Z1 = 10 Ω, Z2 = 12 Ω e Z3 = 20 Ω. Calcule: a) as
corrente de fase e, b) a corrente no neutro.
Sistemas Trifásicos
Resolução:
a) IA= (120V0º) /10 = 12A 0º =12A
IB= (120V -120º) /12 = 10A -120º = -5 – j8,67 (A)
IC= (120V 120º) /20 = 6A 120º = -3 + j5,20 (A)
b) A corrente no neutro é a soma das três correntes acima
IN = IA + IB + IC
IN = 12 + (-5 – j8,67) + (-3 + j5,20)
IN = 4 – j 3,47 = 5,30 -40,9º A
Sistemas Trifásicos
Ligação Triângulo ou Delta
Na ligação triângulo as extremidades dos
enrolamentos do gerador são interligadas de forma
a formar um triangulo.
Sistemas Trifásicos
No circuito da figura abaixo tem-se:
• Corrente de linha (IL), a corrente que circula na linha que liga a carga ao gerador.
• Corrente de fase (IF), a corrente que circula em cada fase da carga (IAB, IBC, ICA).
• Tensão de fase (VF), tensão aplicada nos terminais de cada gerador.
• Tensão de linha (VL), tensão entre duas linhas que conectam a carga ao gerador.
Observar que neste caso VL=VF.
Pode-se demonstrar que a relação entre a corrente de linha e a corrente de fase neste
circuito é dada por:
SISTEMAS TRIFÁSICOS
1, 2 e 3 são os ângulos de defasagem entre a tensão e a
corrente em cada fase. No caso de cargas balanceadas
1=2=3= ,
IAB = IBC = ICA= If
I A = I B = IC = Il
Sistemas Trifásicos
No circuito as tensões de fase valem:
VAB=3800º(V), VBC=380-120º(V) e
VCA=380V120º (V). A carga é balanceada
e resistiva valendo 20 Ω. Pede-se
determinar: a) Corrente de fase de cada
carga. b) Correntes de linha.
Solução:
a) Em cada carga a corrente valerá
IAB=(380  0º)/20 Ω = 19  0º (A)
IBC = (380  -120º)/20 Ω = 19  -120º (A) = -9,5 - j16,45 (A)
ICA = (380  120º) / 20 Ω = 19  120º (A) = -9,5 + j16,45 (A)
b) Correntes de linha
IA = IAB - ICA = 19-(-9,5 +j16,45) = 28,5 -j16,45 = 32,9  -30º (A)
IB =IBC - IAB = (- 9,5 -j16,45)-19 = -28,5-j16,45 =32,9  -150º (A)
IC = ICA - IBC = (-9,5 +j16,45)-(-9,5 -j16,45) =j32,9 = 32,9  90º (A)
Sistemas Trifásicos
A tensão de linha aplicada a um motor cujos enrolamentos
tem 20 Ω de impedância é 220 V. Calcule as correntes de
linha e as correntes de fase se o motor é ligado em
triângulo.
Sistemas Trifásicos
Apesar do motor ter sido projetado para uma tensão de
220 V, ele pode ser ligado a uma tensão de linha de 380 V,
se seus enrolamentos forem ligados em estrela.
Os enrolamentos trabalharão nas mesmas condições quando
ligados em triângulo. Por isso, a maioria dos motores permite
o acesso aos seis terminais dos enrolamentos. Assim, se na
placa do motor estiver escrito 220/380 V, significa que os
enrolamentos devem ser ligados em triângulo se a tensão de
linha é 220 V e ligados em estrela para 380 V.
Sistemas Trifásicos
Um aquecedor trifásico é ligado em estrela e a uma
tensão de linha de 208V. Calcular a corrente de linha.
Sistemas Trifásicos
Repetir o exercício anterior
ligada em triangulo.
supondo que a carga está
Na carga triangulo, a corrente de linha será 3 vezes
maior que na carga estrela , quando ligadas na mesma
tensão.
Sistemas Trifásicos
Potência em sistemas trifásicos
Sistemas Trifásicos
Potência em sistemas trifásicos
Sistemas Trifásicos
Potência em sistemas trifásicos
Sistemas Trifásicos
Potência em sistemas trifásicos
1) Dado o circuito a seguir, pedem-se:
a) Tensões de fase e de linha;
b) Correntes de fase, de linha e no neutro;
c) Potência ativa dissipada.
a) 220V, 381 V
b) 22 A, 22 A, 0
c) 14,52 kW
Sistemas Trifásicos
Potência em sistemas trifásicos
2) A potência de um motor trifásico é 8 kW quando
ligado a uma tensão de linha de 380 Vrms. Calcular a
corrente de linha se o fator de potência é 0,85.
Sistemas Trifásicos
Potência em sistemas trifásicos
3) Um aquecedor trifásico é constituído de três
resistências de 20 Ω ligadas em estrela. Calcular a
corrente de linha e a potência ativa total se a tensão de
linha é 220 Vrms.
IL = IF = 6,35 A
P = 2,42 kW
Sistemas Trifásicos
Potência em sistemas trifásicos
4) Os enrolamentos de um motor tem resistência de 6 Ω
e reatância indutiva de 8 Ω. Sabendo-se que o motor é
ligado em estrela e que a tensão de linha é 220 Vrms,
calcular:
a- correntes de linha e de fase;
b- potências ativa e aparente.
a- 12,7 A
b- 2,9 kW e 4,84 kVA
Sistemas Trifásicos
Potência em sistemas trifásicos
5) Idem ao exercício anterior considerando o motor
ligado em triângulo.
a- 38,1 A
b- 8,71 kW e 14,52 kVA