Aula 05 - Solução

Aula 05
Assuntos:
· Hidrostática
· Calorimetria
· Ondulatória
· M.R.U.V
1.
· Força elétrica
· Magnetismo
· Instrumentos elétricos
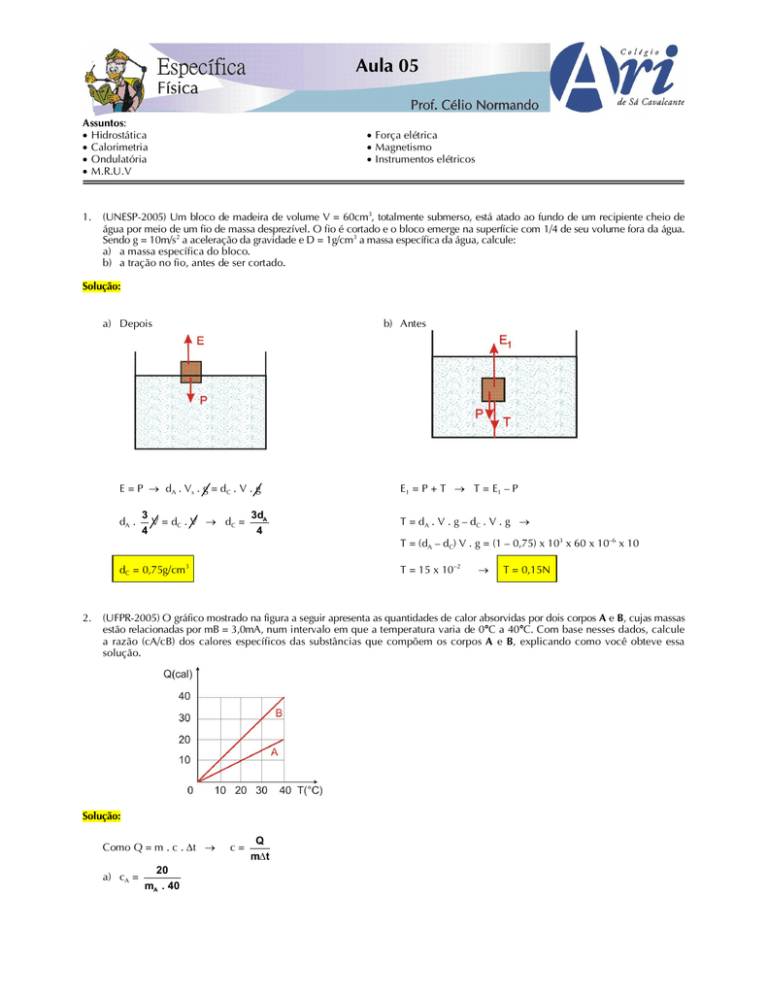
(UNESP-2005) Um bloco de madeira de volume V = 60cm3, totalmente submerso, está atado ao fundo de um recipiente cheio de
água por meio de um fio de massa desprezível. O fio é cortado e o bloco emerge na superfície com 1/4 de seu volume fora da água.
Sendo g = 10m/s2 a aceleração da gravidade e D = 1g/cm3 a massa específica da água, calcule:
a) a massa específica do bloco.
b) a tração no fio, antes de ser cortado.
Solução:
a) Depois
b) Antes
E = P ® dA . Vs . g = dC . V . g
dA .
3 3 d A
V = dC . V ® dC =
4
4 E1 = P + T ® T = E1 – P
T = dA . V . g – dC . V . g ®
T = (dA – dC) V . g = (1 – 0,75) x 103 x 60 x 10–6 x 10
dC = 0,75g/cm3
2.
T = 15 x 10–2
®
T = 0,15N
(UFPR-2005) O gráfico mostrado na figura a seguir apresenta as quantidades de calor absorvidas por dois corpos A e B, cujas massas
estão relacionadas por mB = 3,0mA, num intervalo em que a temperatura varia de 0°C a 40°C. Com base nesses dados, calcule
a razão (cA/cB) dos calores específicos das substâncias que compõem os corpos A e B, explicando como você obteve essa
solução.
Solução:
Como Q = m . c . Dt ®
a) cA =
20 m A . 40 c=
Q m Dt
Aula 05
b) cB =
40 3 m A . 40 c A 20 3 x 40 m A
=
x c B 40 m A 40
3.
®
c A = 15 ,
c B
(UNICAMP-2005) Numa antena de rádio, cargas elétricas oscilam sob a ação de ondas eletromagnéticas em uma dada
freqüência. Imagine que essas oscilações tivessem sua origem em forças mecânicas e não elétricas: cargas elétricas fixas em
uma massa presa a uma mola. A amplitude do deslocamento dessa "antena-mola" seria de 1mm e a massa de 1g para um rádio
portátil. Considere um sinal de rádio AM de 1000kHz.
a) Qual seria a constante de mola dessa "antena-mola"? A freqüência de oscilação é dada por f =
1 2p
k , onde k é a
m
constante da mola e m a massa presa à mola.
b) Qual seria a força mecânica necessária para deslocar essa mola de 1mm?
Solução:
R | p = 9 . m S ƒ = 10 Hz |T m = 10 kg
2 1 ƒ=
2p
a)
k m
®
1
k ƒ =
x ®
4 p 2 m
2
2
k = 4p . ƒ
2
6 -3 k = 3,6 x 1010N/m
b) ƒ = k . x ®
4.
ƒ = 3,6 x 1010 x 10–3
®
ƒ = 3,6 x 107N
(CEFET/CE-2005) O gráfico abaixo representa a velocidade escalar, em função do tempo, de uma partícula que se movimenta
em uma trajetória retilínea com aceleração escalar constante.
Mostre que (v2)2 = (v1)2 + 2 . a . d
Onde a é a aceleração da partícula e d o seu deslocamento entre os instantes t1 e t2.
Solução:
A=d=
tg a
N
a.d=
b V + V gDt 2 1 2
a ®
a =
e V - V i
2 b V + V g Dt x b 2 1 2
2ad = V 2 2 - V 1 2 ®
2
1 Dt V 2 - V1 g
Dt V 2 2 = V 1 2 + 2ad OSG 4621/06
Aula 05
5.
(UFAL-2005) Duas cargas puntiformes Q1 e Q2 estão separadas por uma distância d e se repelem com uma força de
intensidade F.
a) Quando se dobram as duas cargas, qual deverá ser a distância entre elas para que a força de repulsão tenha a mesma
intensidade?
b) Quando se reduz à metade uma das cargas e também a distância entre as duas, qual será a intensidade da nova força de
repulsão?
Solução:
a) 1ª situação: F =
2ª situação: F =
k . Q Q 1 2 d1 2 kQ Q 1 2 d 1 2 4 KQ Q 1 2 ®
d 2 2 d 2 2 = 4d 1 2 ®
k . 2 Q 1 . 2 Q 2 d22 d2 = 2d1
b) 1ª situação: F 1 =
k . Q Q 1 2 d 2
k 2ª situação: F 2 =
6.
F 1 kQ Q 2 d 2 1 2 =
x ®
2 F 2 d 4kQ Q 1 2 F2 = 2F1
Q 1 . Q 2 2 2 d 4
(UFGO-2005) Para medir a intensidade de um campo magnético uniforme, utiliza-se o aparato ilustrado na figura abaixo.
O fio condutor tem comprimento 2,5cm e massa 2,0g; as molas, condutoras de eletricidade, têm constante elástica 5,0N/m. Quando
a tensão elétrica está desligada as molas apresentam deformação de 2,0mm. Com a tensão ajustada para produzir uma corrente de
1,0A, as molas retornam ao estado natural. Dado que o campo magnético é perpendicular ao plano da figura, determine a sua
magnitude e o seu sentido. Despreze os efeitos da corrente e do campo sobre as molas.
Solução:
Situação inicial ® molas deformadas – circuito sem corrente elétrica
2ƒ = P ® 2kx = M.g
3
OSG 4621/06
Aula 05
Situação final ® molas sem deformação – circuito com corrente elétrica
FM = P ® B . i . L = Mg
B . i . L = 2kx ® B =
B = 0,80T
7.
2 kx 2 . 5 . 2 . 10 -3 =
i . L 1 . 2, 5 . 10 -2 entrando no plano do papel
(UNESP-2005) Uma partícula, de volume V e de massa m, está em queda em um meio líquido. Considerando-se desprezíveis
os efeitos de viscosidade do líquido no movimento da partícula,
a) represente o diagrama de forças que atuam sobre a partícula nessa situação.
b) determine o módulo da aceleração da partícula em função da densidade da partícula pp, da densidade do líquido PL, e da
aceleração gravitacional g.
Solução:
a)
b) P – E = m . a
PP . V . g – PL . V . g = PP . V . a
a=
8.
b P - P g g P L P P
(UFGO-2005) No circuito abaixo, a fonte de tensão U, o voltímetro V e o amperímetro A são ideais.
Variando os valores da tensão na fonte e medindo a diferença de potencial no voltímetro e a corrente no amperímetro, construiuse o gráfico abaixo.
4
OSG 4621/06
Aula 05
Calcule a resistência equivalente do circuito.
Solução:
·
·
·
Voltímetro: mede a tensão nos resistores 2R e 3R
Amperímetro: mede a corrente no resistor 2R
150 Cálculo de 2R ® tg a 2 R =
® 2R = 100 ® R = 50W
15
,
Cálculo da resistência equivalente
2 R x 3 R 6 R 11 R Re = R +
® R e = R +
® R e =
2 R + 3 R 5 5 N
Re =
11 x 50 ®
5 Re = 110W
5
OSG 4621/06