quadriláteros

QUADRILÁTEROS
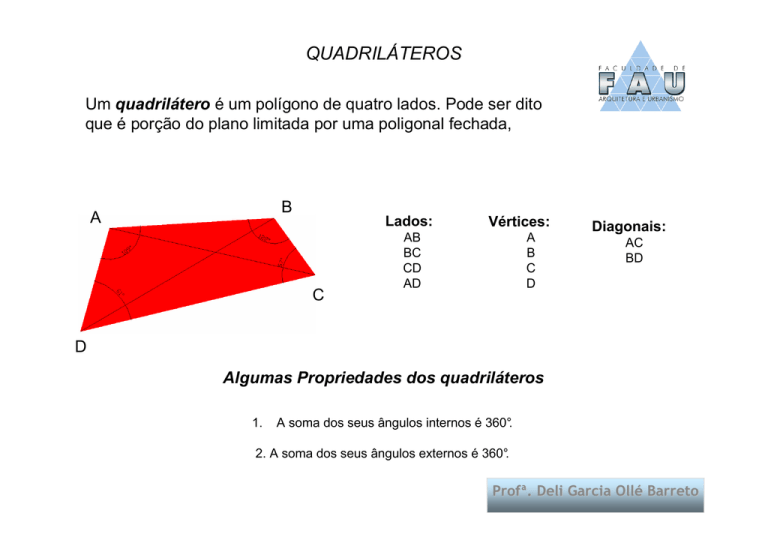
Um quadrilátero é um polígono de quatro lados. Pode ser dito
que é porção do plano limitada por uma poligonal fechada,
B
A
Lados:
C
Vértices:
AB
BC
CD
AD
A
B
C
D
Diagonais:
AC
BD
D
Algumas Propriedades dos quadriláteros
1.
A soma dos seus ângulos internos é 360°.
2. A soma dos seus ângulos externos é 360°.
Profª. Deli Garcia Ollé Barreto
Classificação dos Quadriláteros
a) Paralelogramo
Chama-se paralelogramo o quadrilátero que possui lados paralelos dois a dois (lados opostos paralelos).
Propriedades dos Paralelogramos
•
•
Seus lados e seus ângulos opostos são congruentes.
Suas diagonais se cortam no ponto médio.
Classificação dos paralelogramos
1. No quadrado
•As diagonais são iguais e perpendiculares nos seus pontos médios.
•Todos os ângulos interno são retos.
•Seus lados são iguais.
QUADRADO
•O quadrado pose ser inscrito numa circunferência de raio igual a sua
semi diagonal.
Profª. Deli Garcia Ollé Barreto
No retângulo
• As diagonais são oblíquas, iguais e se cortam
nos seus pontos médios.
•Todos os ângulos interno são retos.
•Seus lados opostos são iguais.
RETÂNGULO
•O retângulo pose ser inscrito numa circunferência de raio igual a
sua metade da diagonal.
No losango
• As diagonais são diferentes, perpendiculares, se cortam nos seus
pontos médios e são bissetrizes dos ângulos internos.
•Nenhum ângulo interno é reto.
LOSANGO
•Seus lados são iguais.
•Não é inscritível.
No paralelogramo
• As diagonais são diferentes, oblíquas e se cortam nos seus pontos
médios.
•Nenhum ângulo interno é reto.
•Seus lados opostos são iguais.
PARALELOGRAMO
•Não é inscritível.
Profª. Deli Garcia Ollé Barreto
b) Trapézio
Chama-se trapézio o quadrilátero que possui somente dois lados opostos paralelos
e estes recebem a denominação de bases do trapézio.
Apresenta dois
ângulos de 90°
Trapézio Retângulo:
Os lados opostos não paralelos são congruentes
As diagonais são congruentes
Os ângulos de uma mesma base são congruentes
Trapézio Isósceles
Profª. Deli Garcia Ollé Barreto
Os lados opostos não
paralelos, não são
congruentes
Trapézio Escaleno
Profª. Deli Garcia Ollé Barreto
EXERCÍCIOS
Desenhar um quadrado de
diagonal = 65 mm
Desenhar uma circunferência de diâmetro igual a
diagonal e inscrever o quadrado nesta
circunferência.
Desenhar um quadrado
de lado = 40 mm
Desenhar perpendiculares pelos extremos do lado
e sobre estas marcar o valor do lado. (não usar
esquadros nas construções).
Profª. Deli Garcia Ollé Barreto
Desenhar um quadrado sabendo
que a somo da diagonal e do lado
é igual a 55 mm.
D
Desenhar um retângulo conhecendo
os dois lados, simultaneamente 40
mm e 20 mm.
C
C
A
B
E
A
B
•Desenhar quadrado de lado AB qualquer:
•Acrescentar, sobre a mesma reta suporte da
diagonal e a partir de seu extremo, o valor do lado
obtendo o ponto C:
•Unir o ponto C ao Ponto B:
•Marcar, a partir do ponto A e sobre a reta suporte
da diagonal, o valor 55 mm (diagonal + lado do
quadrado que se quer desenhar) obtendo o ponto
D;
•Pelo ponto D traçar uma paralela ao segmento BC
obtendo o ponto E;
•AE é o lado do quadrado proposto.
•Desenhar um dos lados, por exemplo AB, e por
um dos extremos levantar uma perpendicular;
•Sobre a perpendicular marcar o valor do outro
lado obtendo o ponto C;
•O segmento AC é o diâmetro da circunferência
que inscreve o retângulo.
Profª. Deli Garcia Ollé Barreto
Desenhar o losango de diagonal =
50 mm e lado = 30 mm
Desenhar o trapézio retângulo de
bases 50 e 20 mm, sabendo que sua
altura é 30 mm.
•Desenhar uma reta e sobre ela marcar 50 mm
(diagonal do losango;)
•Desenhar uma reta e sobre ela marcar 50 mm
(base maior);
•Centrar o compasso nos seus extremos e traçar
arcos de raio = 30 mm (lado do losango);
•Por um de seus extremos levantar uma
perpendicular de 30 mm (altura);
•As intersecções dos arcos são os dois outros
vértices do quadrilátero.
•Pelo extremo da perpendicular traçar uma paralela
a base;
•Sobre esta paralela marcar 20 mm (base menor).
Profª. Deli Garcia Ollé Barreto
Desenhar o trapézio isósceles com os seguintes dados:
Base maior = 50 mm; Base menor = 30 mm e Altura = 30 mm.
•Desenhar uma reta e sobre ela marcar 50 mm
(base maior);
•Por um de seus extremos levantar uma
perpendicular de 30 mm (altura);
•Pelo extremo da perpendicular traçar uma paralela
a base;
•Sobre esta paralela marcar 20 mm (base menor).
Profª. Deli Garcia Ollé Barreto