Tensão - Chasqueweb

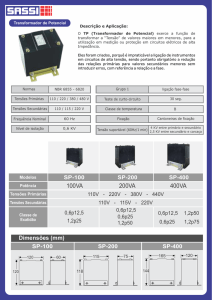
ENG01140 – Turma C (Prof. Alexandre Pacheco)
11
32
TENSÃO
Tensão Normal e Tensão Cisalhante:
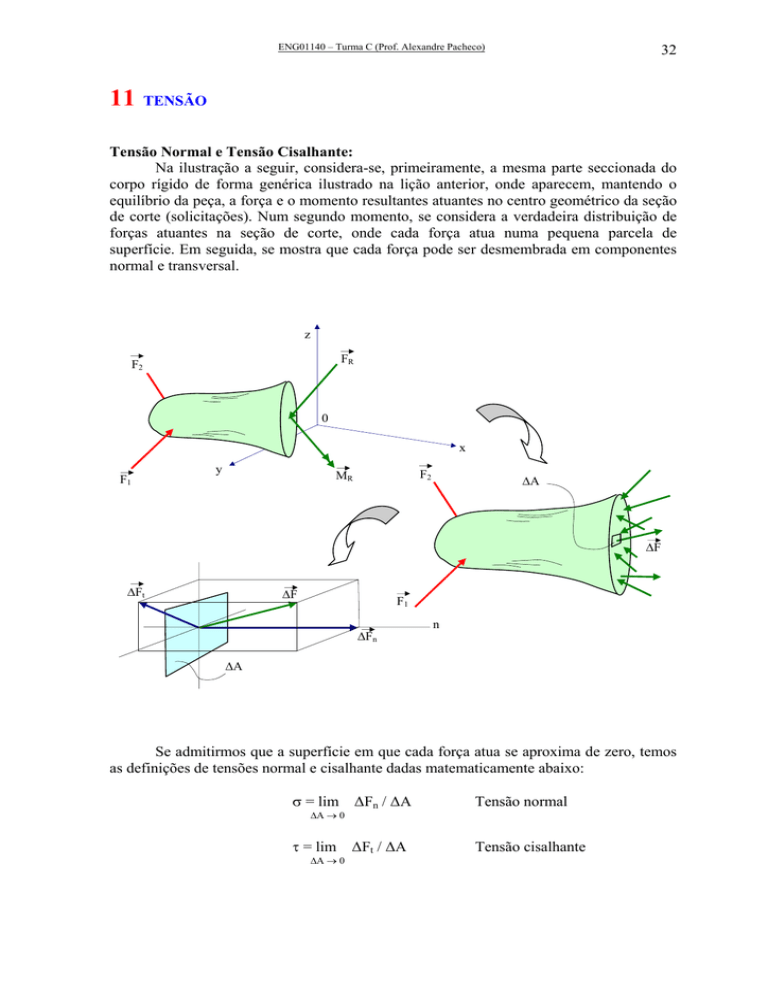
Na ilustração a seguir, considera-se, primeiramente, a mesma parte seccionada do
corpo rígido de forma genérica ilustrado na lição anterior, onde aparecem, mantendo o
equilíbrio da peça, a força e o momento resultantes atuantes no centro geométrico da seção
de corte (solicitações). Num segundo momento, se considera a verdadeira distribuição de
forças atuantes na seção de corte, onde cada força atua numa pequena parcela de
superfície. Em seguida, se mostra que cada força pode ser desmembrada em componentes
normal e transversal.
z
FR
F2
0
x
F1
y
F2
MR
∆A
∆F
∆Ft
∆F
F1
∆Fn
n
∆A
Se admitirmos que a superfície em que cada força atua se aproxima de zero, temos
as definições de tensões normal e cisalhante dadas matematicamente abaixo:
σ = lim ∆Fn / ∆A
Tensão normal
τ = lim ∆Ft / ∆A
Tensão cisalhante
∆A → 0
∆A → 0
ENG01140 – Turma C (Prof. Alexandre Pacheco)
33
Componentes Cartesianas da Tensão:
Ao se considerar um sistema cartesiano de coordenadas para as áreas de atuação de
cada força, obtêm-se as componentes de tensão associadas àquela área:
x
x
τzx
∆Fx
∆F
z
∆Fz
∆Fy
y
y
z
τzy
σz
∆A
Realizando-se outro seccionamento, perpendicular ao corte anterior, e procedendose de forma idêntica, obtemos três mais componentes de tensão:
∆A
∆F
x
∆Fx
∆F
∆F1
∆Fz
σx
∆Fy
τxz
τxy
τzy
z
y
τzx
σz
Assim, com quatro seccionamentos adicionais, obtém-se o cubo de arestas
infinitesimais abaixo onde, em cada uma de suas faces, aparecem três componentes de
tensão:
σx
τxz
τzx
τxy
τyx
σz
τyz
σy
τzy
ENG01140 – Turma C (Prof. Alexandre Pacheco)
34
As tensões com sentidos positivos definem completamente o Estado de Tensões no
Entorno de um Ponto, pois, por Superposição de Efeitos, temos:
σz ∆A
τzy ∆A
τzx ∆A
z
τxz ∆A
τxy ∆A
τyz ∆A
τyx ∆A
σx ∆A
σy ∆A
x
y
τzy ∆A
σz ∆A
τ´xy ∆A
τzx ∆A
τ´yx ∆A
τ´yz ∆A
σ´y ∆A
σ´x ∆A
σx ∆A
σy ∆A
τ´zy ∆A
τyz ∆A
σ´z ∆A
τ´xz ∆A
τxz ∆A
τxy ∆A
τ´zx ∆A
τyx ∆A
de onde, por equilíbrio, se tira que apenas seis tensões são independentes e, por
conseguinte, são suficientes para definir o estado de tensões no entorno de um ponto:
σx = σ´x
σy = σ´y
σz = σ´z
τzy = τ´zy = τ´yz = τyz
τzx = τ´zx = τ´xz = τxz
τxy = τ´xy = τ´yx = τyx
z
σz
τzx
τxz
σx
x
σx τxy τxz
σ=
σ τ
~ sim. y yz
σz
τzy
τyz
σy
τxy τyx
y
ENG01140 – Turma C (Prof. Alexandre Pacheco)
35
Tensão Normal Média:
Na ilustração abaixo, um cilindro, primeiramente sem esforços aplicados e,
portanto, indeformado, é submetido a uma carga de tração. Nas regiões mais próximas aos
pontos de aplicação da carga, as deformações são mais visíveis, com grandes
concentrações de seus efeitos em determinados pontos (concentrações de tensão). Longe
destas regiões, à meia-altura do cilindro, percebe-se que linhas traçadas ao longo do
mesmo sofrem menos perturbações, caracterizando uma região onde as deformações se
processariam de um modo muito mais uniforme. Nesta região, o valor médio das tensões é
um valor bastante representativo das tensões que ali ocorrem, e a fórmula dada abaixo
ganha grande significância. Próximo das cargas, no entanto, o valor médio das tensões
normais perde esta significância, pois os picos de tensões são muito mais intensos,
podendo romper o material de que é feito o cilindro muito antes da tensão de tração normal
média medida chegar no seu valor crítico.
P
A
σ=
N
A
Região de
deformação
uniforme
(N = P)
P
P
Tensão Cisalhante Média:
Na figura a seguir, têm-se, num primeiro momento, três chapas unidas conforme
ilustrado. Num segundo momento, um carregamento é aplicado perpendicularmente ao
conjunto, fazendo com que reações que configuram esforços de corte apareçam em
conseqüência da geometria do conjunto. Este esforço cortante deve estar, naturalmente,
em equilíbrio com as tensões cisalhantes que irão se processar na seção transversal
mostrada na figura.
Tanto a face superior quanto a inferior da chapa seccionada não estão sendo
exigidas por nenhum carregamento nos seus planos e, por conseguinte, devem apresentar
tensões de cisalhamento nulas. Assim, de forma que o equilíbrio de cubos elementares
porventura retirados das arestas formadas no encontro daquelas faces com a face vertical
não seja violado, tem-se que os valores de tensões cisalhantes nesta face também devem,
obrigatoriamente, ser nulos como ilustrado.
ENG01140 – Turma C (Prof. Alexandre Pacheco)
36
P
P
A
V = P/2
τ=
V
A
Conclui-se, portanto, que a integral das tensões cisalhantes na face vertical só será
igualada ao esforço cortante se a tensão cisalhante alcançar um valor máximo na região
central da face vertical, como indicado. Se a espessura da chapa seccionada por
suficientemente pequena, um valor médio das tensões dado pela expressão em dada acima
será bastante representativo das tensões cisalhantes reais. Na medida que a espessura
aumenta, no entanto, o erro vai aumentando, ou seja, a diferença entre a tensão cisalhante
máxima e a tensão cisalhante média ficará cada vez mais importante. Assim, o uso da
expressão acima para o cálculo de tensões cisalhantes é considerado convencionalmente
(Tensão Cisalhante Convencional) para elementos de seção transversal reduzida, onde o
erro mencionado pode ser desprezado. Este é o caso das seções cisalhantes que se
processam, principalmente, em elementos tais como parafusos, pregos, rebites, e etc.
Tensões Admissíveis:
Fator de segurança (F.S.) = Pfalha / Padm ≥ 1
Para um sistema linear, onde há a linearidade entre cargas e tensões, o fator de
segurança FS pode também ser usado como abaixo, relacionando tensões de falha com
tensões admissíveis de projeto:
FS = σfalha / σadm = τfalha / τadm ≥ 1